"Push yourself, because no one else is going to do it for you." - Unknown

1. 题目描述

2. 题目分析与解析
2.1 思路一——暴力求解
之所以先暴力求解,是因为我开始也没什么更好的思路,所以就先写一种解决方案,没准写着写着就来新的灵感了。暴力求解思路还是很简单的,就是尝试遍历面板的每个格子,判断其周围八个位置的状态(对于边角需要特殊处理),根据边角种存在的活细胞(也就是1的个数)判断该位置应该填什么。

但是需要注意一点,为了避免我们在原矩阵上更改值后导致影响后续的判断,所以我们肯定需要先复制一个原始矩阵。
代码思路:
-
初始化,复制一个原始矩阵
-
遍历复制矩阵的每一个元素,查看其周围八个位置的状态,统计1的个数
-
根据题目提到的判定规则:少于 2 个或者大于 3 个 1 就判定当前位置为 0
-
等于 2 个 1 那么当前位置不需要更改
-
如果等于 3 个 1 那么当前位置如果为 0 需要改为 1
-
对于边角位置需要额外处理防止越界
-
2.2 思路二——进阶(原地算法)

根据题目中的进阶提示,要求使用原地算法,也就是不能用一个额外的面板存储现有的值,并且还提示了所有格子被同时更新。因此我们再想一想怎么解决。
如果使用原地算法,最主要的问题就是对于前面内容的更新会影响后面的结果,因为你不知道原来前面的内容是什么样子。但是记住,原始状态只有两种,要么是0,要么是1。
而变化也只有四种
-
要么原来是0,后来变成1
-
要么原来是0,保持不变为0
-
要么原来是1,后来变成0
-
要么原来是1,后来不变为1
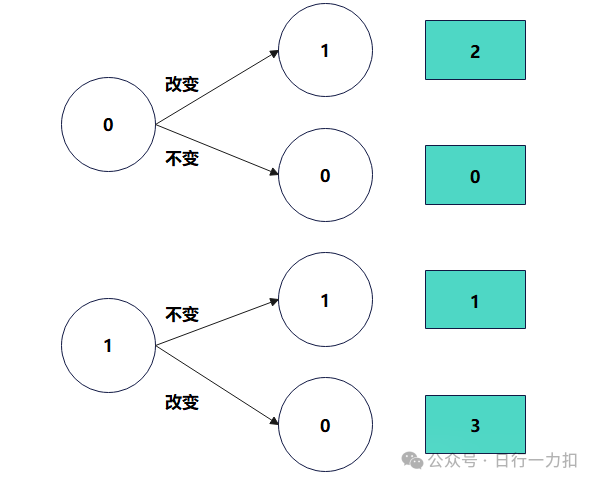
如下图:

因为我们担心原始信息被覆盖,因此我们是不是可以添加几个数字也就相当于几种状态,来存储这些被覆盖的信息?这样我们看见某一个数字就知道它之前是什么状态,就相当于在原始数据的基础上进行操作了!在这里我们假设:
-
用 0 和 1 还是表示原来是什么现在就是什么的情况,也就是对应上图中两种不变的情况
-
而用数字2表示 0 改变为 1
-
用数字3表示 1 改变为 0
作图表示如下:
对于这种原地算法,如果你需要用到之前的信息,但是可能之前的信息会被修改,就想办法把原始信息用一种方式存储起来。
因此我们在遍历面板的每一个元素时,我们就知道之前的位置原始数据是什么,这样就能正确计算结果,等到最后我们再根据每一种数字的情况将它归为正确的表示,比如最后我们处理完了所有数据,然后我们再遍历每个元素:
-
发现值为0或者1就不动
-
发现值为2就变为1
-
发现值为3就变为0
这样就可以得到最终结果!
代码思路:
-
遍历面板每一个元素,根据原始状态和需要改变为的值确定该位置的值
-
对于面板每一个元素,遇见周围八个位置中有1和3就把它当作1
-
对于面板每一个元素,遇见周围八个位置中有2和0就把它当作0
-
-
处理完每个元素后再次遍历整个面板,将1与3替换回正确的值
2.3 思路三——思路一的优化(位运算)
现在我们看看还有没有什么优化空间,有时间提示信息不是白给的哦:
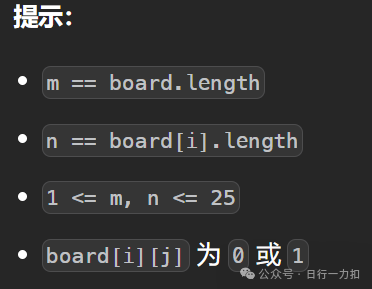
题目提示我们board[i][j] 为 0 或 1,0和1,有没有想到什么?学计算机的0和1分别表示什么?在java中int是怎么存储的?
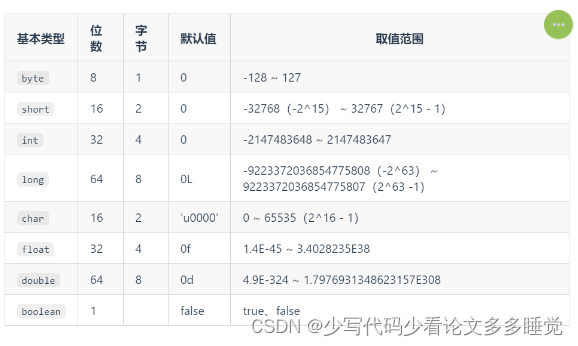
再看看面板的大小?1 <= m, n <= 25,在联想一下int的存储大小:
在不同编程语言中,int 类型的大小可以有所不同。以下是一些常见编程语言中 int 类型的大小:
C/C++:
根据编译器和操作系统的不同,
int类型通常为 4 字节,范围大约是 -2,147,483,648 到 2,147,483,647。Java:
Java 中的
int类型固定为 4 字节,范围是 -2,147,483,648 到 2,147,483,647。Python:
Python 中的
int类型大小是动态的,它可以根据需要自动调整。在 32 位系统上,通常为 4 字节,范围约为 -2,147,483,648 到 2,147,483,647;在 64 位系统上,它可以是 4 字节或 8 字节,取决于所使用的 Python 版本。JavaScript:
JavaScript 中的
int类型实际上是一个 64 位浮点数,范围大约是 -9,007,199,254,740,992 到 9,007,199,254,740,992。Swift:
Swift 中的
Int类型的大小取决于当前平台的位数。在 32 位平台上,Int是 32 位,范围大约是 -2,147,483,648 到 2,147,483,647;在 64 位平台上,Int是 64 位,范围大约是 -9,223,372,036,854,775,808 到 9,223,372,036,854,775,807。
可以看到在大多数情况下至少是按照4字节存储的,也就是32位,而一位可以表示0或者1两个数,联想到这里是不是又有了一种思路?我们是不是可以按照思路一的解决方案,虽然我们copy了一个原始面板,但是我们面板的每一个值都是一个int,如果我们把面板的一行设置位一个int来存储,通过位运算来求解,是不是能省好多空间?
所以代码思路还是思路一的代码思路,但是我们此时需要使用位运算来解决!

如上图,红色部分就相当于我们的面板。
代码思路:
-
设置一个和board数组一样行数的int数组命名位copy,每一个int值表示board的每一行
-
初始化,采用位运算初始化copy数组
-
遍历复制矩阵的每一个元素,查看其周围八个位置的状态,统计1的个数
-
根据题目提到的判定规则:少于 2 个或者大于 3 个 1 就判定当前位置为 0
-
等于 2 个 1 那么当前位置不需要更改
-
如果等于 3 个 1 那么当前位置如果为 0 需要改为 1
-
对于边角位置需要额外处理防止越界
-
2.4 思路四——压榨空间到极致
既然我们已经完成了思路三的代码,我想大家应该更清楚位运算的特点。这时我们再看看面板,面板中每一个位置是不是一个int值?那就是32位(假设java在通常情况下),而面板中的值0或者1肯定只用了最后一位,就像下面这样:

是不是这么多位置都空着想不想做点什么?空着的就是空间啊,由于1 <= m, n <= 25,那么是不是我们就可以用每一行的行首元素来当作我们思路三的copy数组,还是进行位运算操作,但是就不需要额外的空间了。
思路和思路三相似,但是唯一的改变就是我们将copy数组放在了board面板的每一行行行首位置而已。
比如对于题目中的示例:
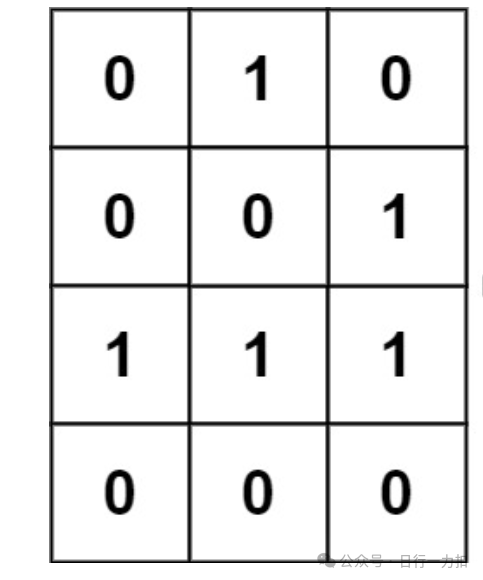
将它放大看就是这样:
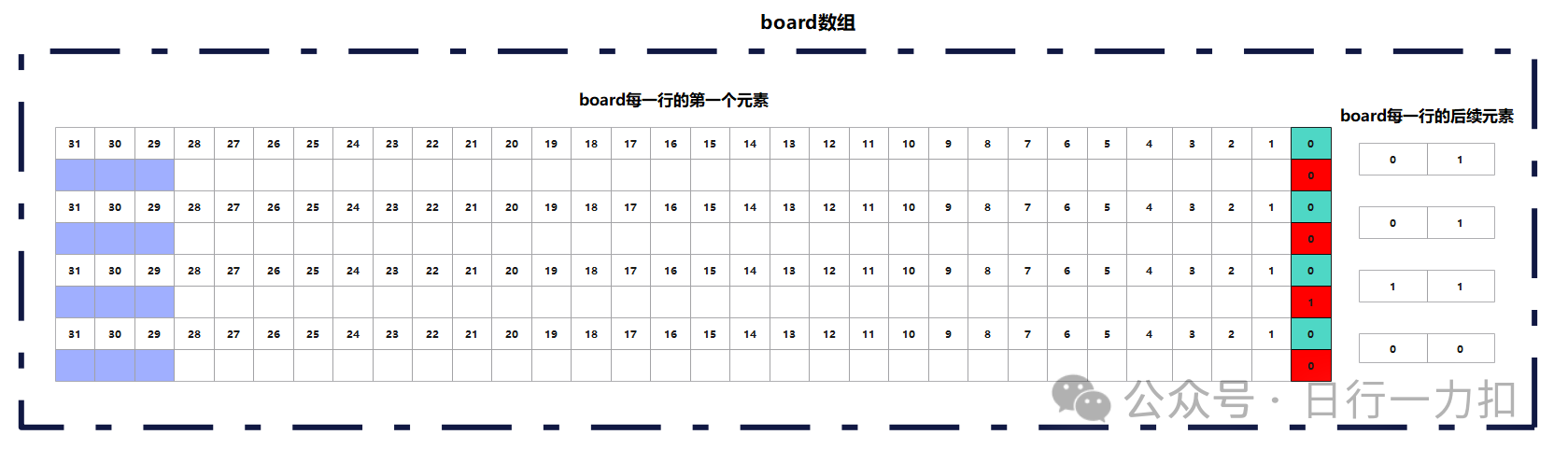
其中蓝色部分就是我们充当copy数组的位置。
比如对于题目中的
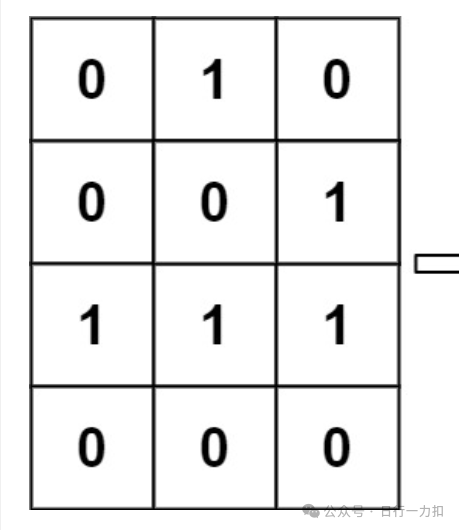
它转化后的结果位:
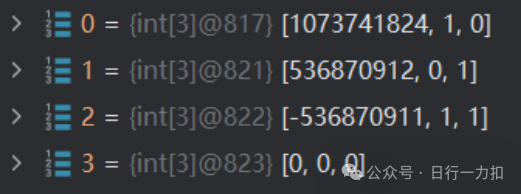
对应的二进制位为:
-
1073741824is represented as01000000000000000000000000000000 -
536870912is represented as00100000000000000000000000000000 -
-536870911is represented as11100000000000000000000000000001 -
0is represented as00000000000000000000000000000000
代码思路:
-
初始化,采用位运算初始化copy数组(实际上就是board的第一个元素的相应位)
-
遍历复制矩阵的每一个元素,查看其周围八个位置的状态,统计1的个数
-
根据题目提到的判定规则:少于 2 个或者大于 3 个 1 就判定当前位置为 0
-
等于 2 个 1 那么当前位置不需要更改
-
如果等于 3 个 1 那么当前位置如果为 0 需要改为 1
-
对于边角位置需要额外处理防止越界
-
-
最后需要更新第一列恢复为原来的值
2.5 思路五——压榨空间到极致2
改代码是看了自在飞花的解释学到的,确实很厉害,因为他写的c++版本,我在这解释一下核心思想,并写一个java版本。
这段代码的核心思路是两遍扫描棋盘:
-
第一遍扫描,计算每个细胞周围活细胞的数量,并用第二个比特位来存储细胞是否应该存活。由于细胞的状态是用0(死)和1(活)来表示的,所以作者通过按位与操作
&1来获取当前细胞的状态,也就是只取int的最后一位,也就是0或者1,仅累加最低位,来计算周围的存活细胞个数。 -
第二遍扫描,通过右移操作
>>= 1来更新细胞的状态。这是因为在第一遍扫描中,如果一个细胞在下一代应该是活的,那么它的第二个比特位将被设置为1。通过右移一位,我们可以用这个第二比特位来覆盖原来的状态,从而更新棋盘。

-
同时在代码中使用了两个数组dx和dy,他们用来表示周围的八个位置,减少了遍历周围八个位置的for循环造成变量
k或者l的重复开辟空间。
这个代码我就直接附在这里了:
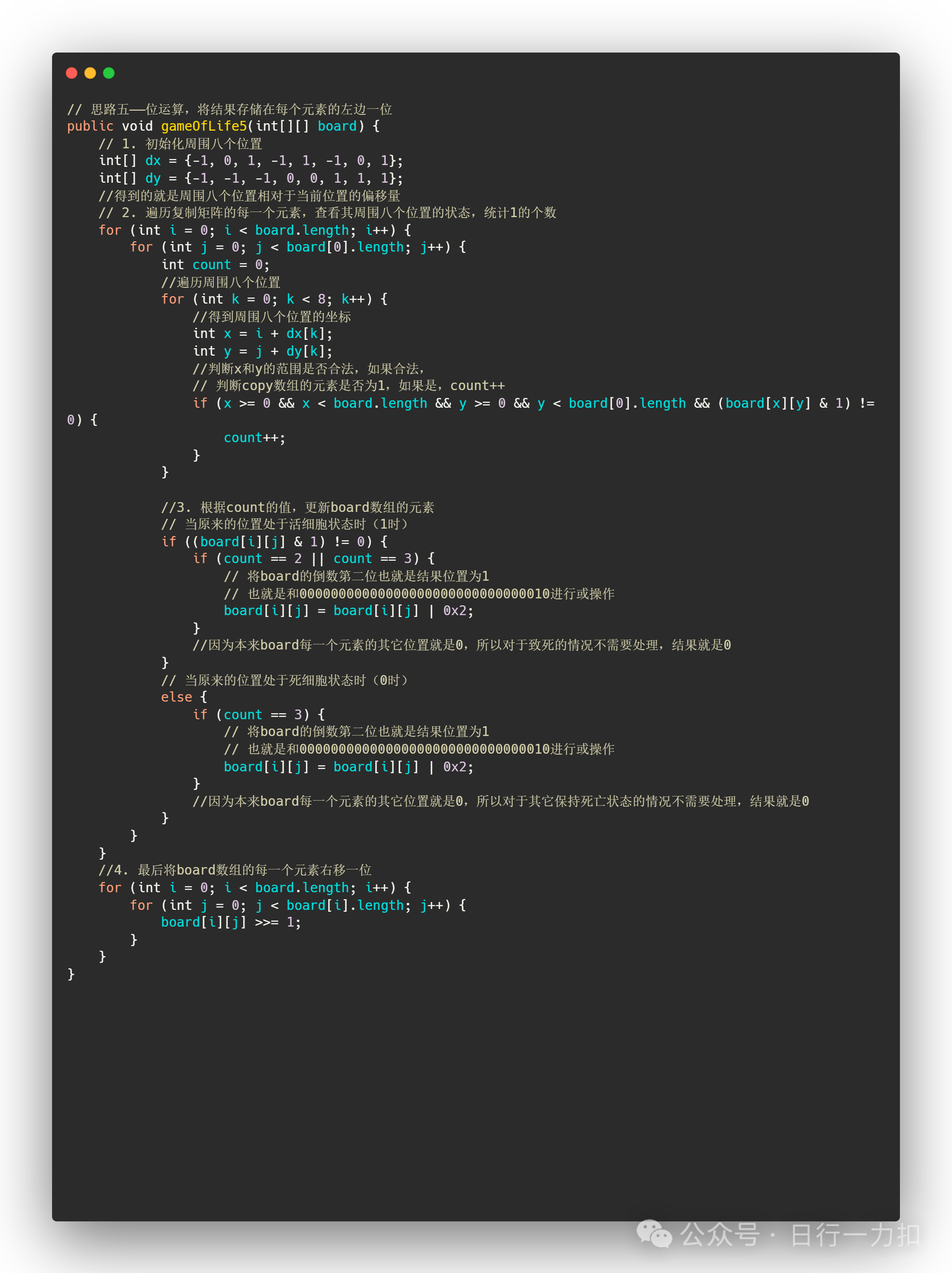
其实效果和思路四差不多,但是思路值得借鉴。
补充
count的优化
如果还想继续优化还是有优化空间的,比如我们的count作为一个计数变量,是可以放在某一个board元素里面的,因为它的最大值不会超过8,因为周围最多也就八个元素。这样用一个3个bit就可以存储起来。
dx和dy优化
同时dx和dy也可以优化,因为dx和dy的范围就是在-1到1之间,因此可以用两个bit来存储一个值,dx和dy总共有8组,也就是16个元素,那么用32个bit就可以存储所有的dx和dy。
当然上面的优化有点太疯狂了,但是我们要举一反三想到这些思路。
3. 代码实现
3.1 思路一——暴力求解

3.2 思路二——原地算法
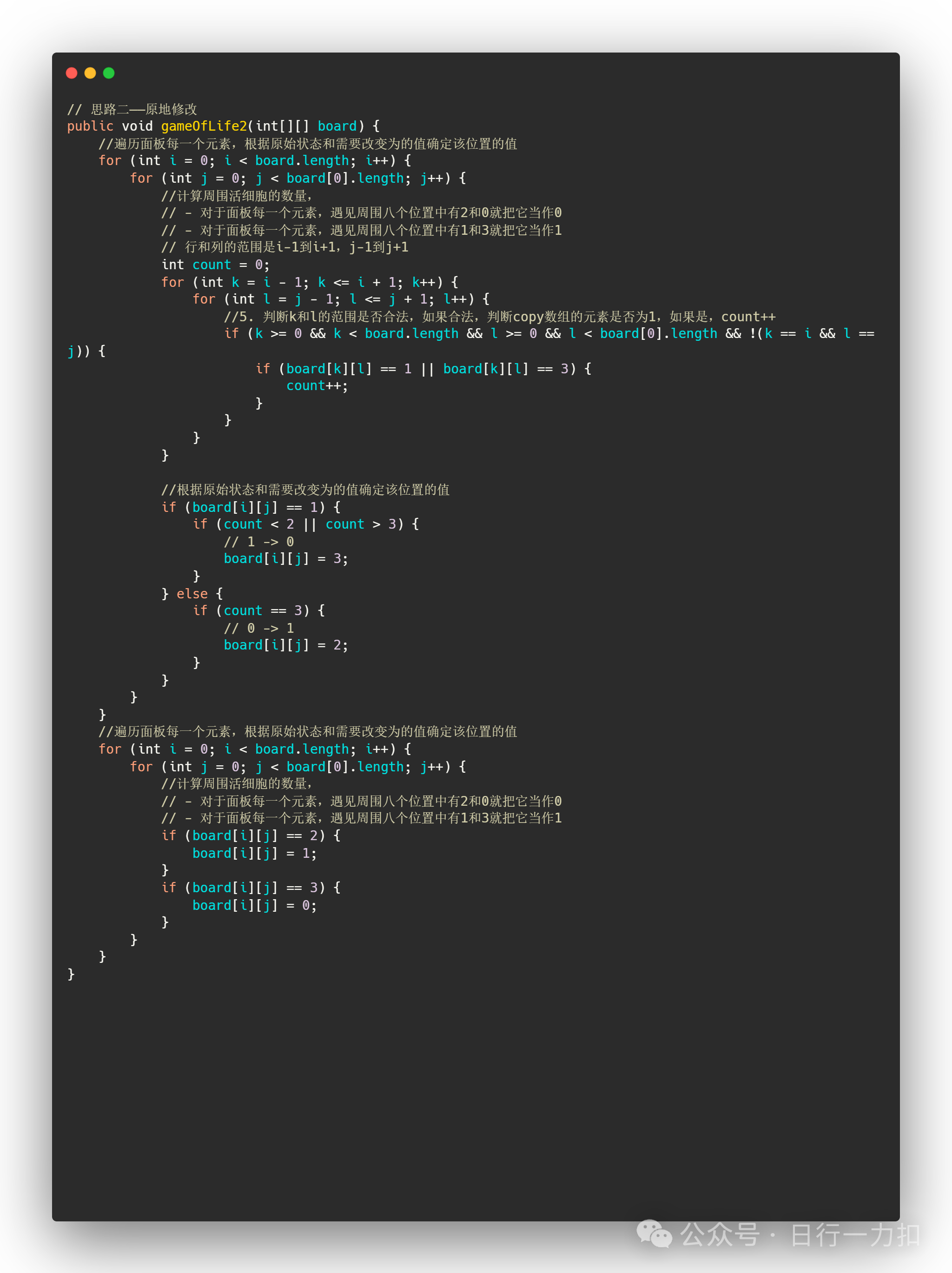
3.3 思路三——优化(位运算)
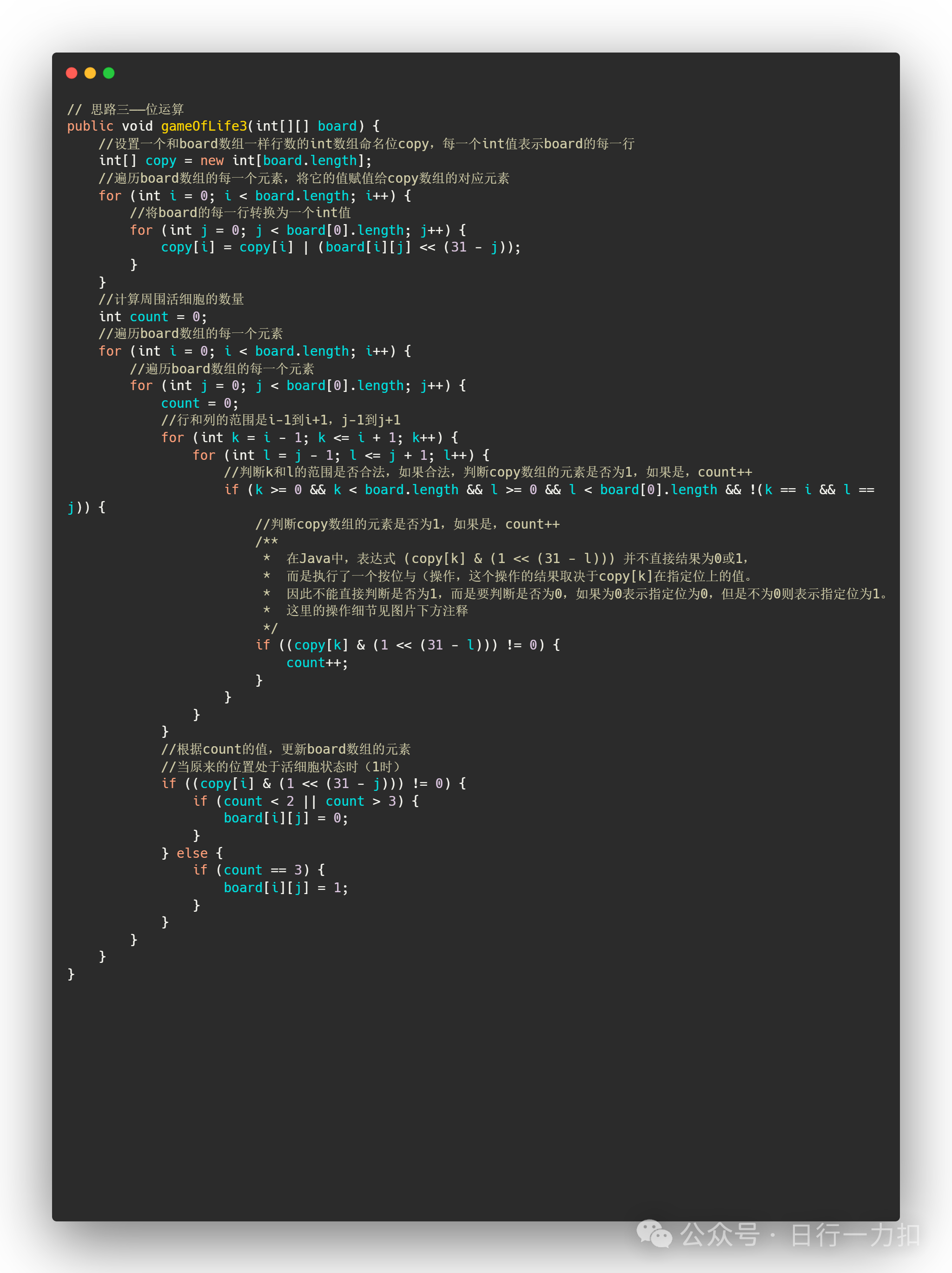
在Java中,表达式 (copy[k] & (1 << (31 - l))) 并不直接结果为0或1,而是执行了一个按位与(&)操作,这个操作的结果取决于copy[k]在指定位上的值。这里的操作细节如下:
1 << (31 - l):这部分是位移操作。它将数字1向左移动(31 - l)位。这意味着,如果l为0,那么1将被移动到最高位(假设是32位整数),如果l是其他值,1就会被移动到相应的位置上。这样做的目的是为了生成一个只在特定位置上有一个1的整数,其他位置都是0。
copy[k] & (1 << (31 - l)):这部分是按位与操作。它比较copy[k]和上面计算出的数值,在每个位上进行逻辑与操作。只有当copy[k]在相应的位上也是1时,这个操作的结果在那个位上才是1,否则结果为0。因此,这个表达式的结果是一个整数,它在大多数位上都是0,在特定的位上可能是0或者是2的某次幂(取决于l的值)。如果你想判断这个操作的结果是否为非零(即判断copy[k]在(31 - l)位上是否为1),你可以将整个表达式与0进行比较:
<span style="background-color:#f8f8f8"><span style="color:#008855">boolean</span> <span style="color:#000000">isBitSet</span> <span style="color:#981a1a">=</span><span style="color:#777777"> (</span><span style="color:#000000">copy</span><span style="color:#777777">[</span><span style="color:#000000">k</span><span style="color:#777777">] </span><span style="color:#981a1a">&</span> <span style="color:#777777">(</span><span style="color:#116644">1 << </span><span style="color:#777777">(</span><span style="color:#116644">31</span> <span style="color:#981a1a">-</span> <span style="color:#000000">l</span><span style="color:#777777">))) </span><span style="color:#981a1a">!=</span> <span style="color:#116644">0</span><span style="color:#777777">;</span></span>如果你的目的是确保结果严格为0或1,你需要进一步处理这个表达式,例如通过判断表达式是否非零来将结果转换为0或1:
<span style="color:#777777"><span style="background-color:#f8f8f8"><span style="color:#008855">int</span> <span style="color:#000000">bitValue</span> <span style="color:#981a1a">=</span> (<span style="color:#000000">copy</span>[<span style="color:#000000">k</span>] <span style="color:#981a1a">&</span> (<span style="color:#116644">1</span> << (<span style="color:#116644">31</span> <span style="color:#981a1a">-</span> <span style="color:#000000">l</span>))) <span style="color:#981a1a">!=</span> <span style="color:#116644">0</span> <span style="color:#981a1a">?</span> <span style="color:#116644">1</span> : <span style="color:#116644">0</span>;</span></span>这样,bitValue就会根据copy[k]在(31 - l)位上是否为1来分别存储1或0。
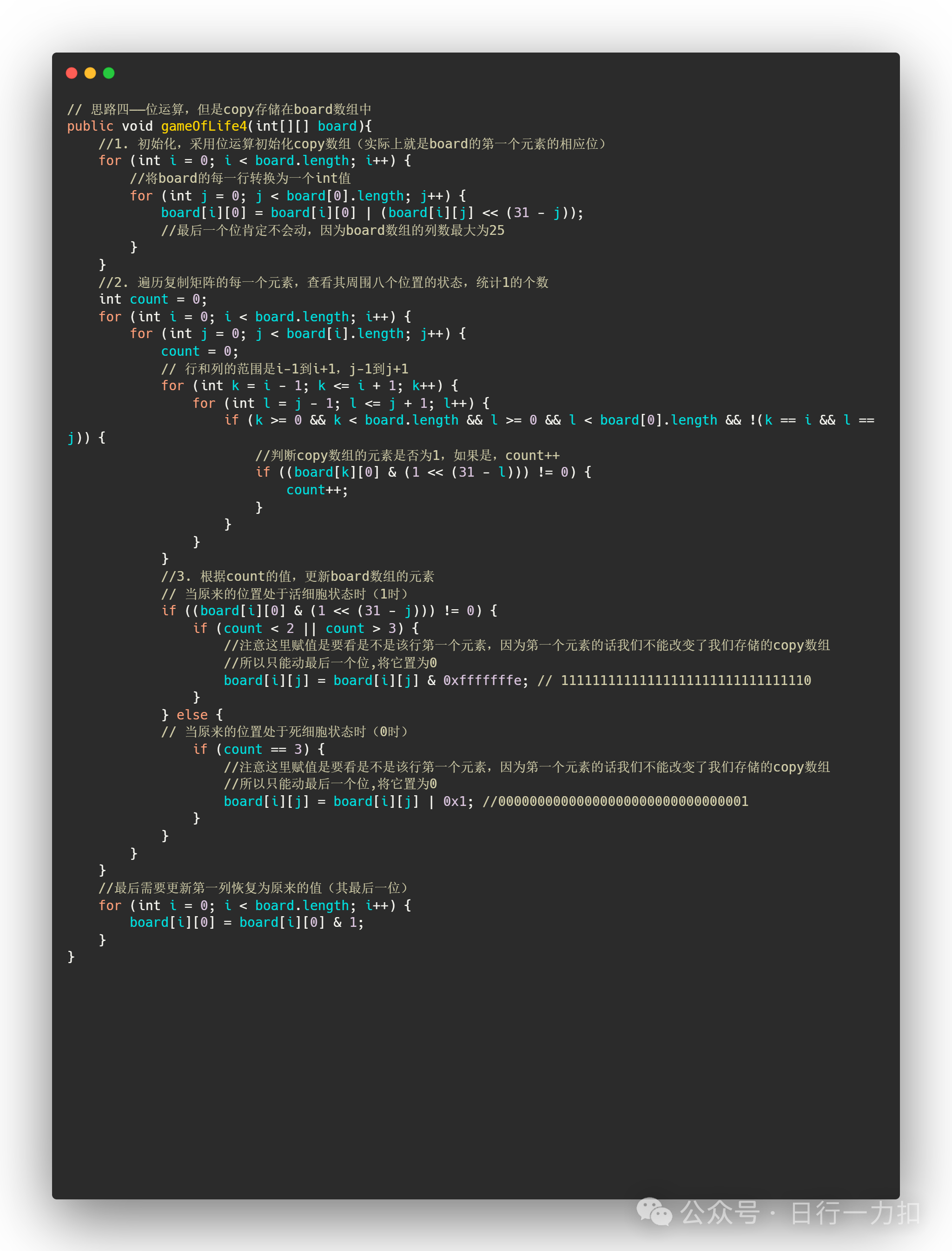
3.4 思路四——位运算,但是copy存储在board数组中
4. 相关复杂度分析
解法一:额外的复制矩阵
时间复杂度:O(MN),其中M是行数,N是列数。因为需要遍历整个矩阵两次,一次复制,一次计算。空间复杂度:O(MN),因为需要一个同样大小的矩阵来存储复制。
解法二:原地修改
时间复杂度:O(M*N),同样需要遍历整个矩阵来计算周围活细胞的数量。空间复杂度:O(1),除了原数组外,没有使用额外的空间,只是利用了额外的状态来标记中间状态。
解法三:位运算
时间复杂度:O(M*N),需要遍历整个矩阵来计算。空间复杂度:O(M),虽然没有使用额外的矩阵,但是使用了一个数组来存储行的状态。
解法四:位运算,但是copy存储在board数组中
时间复杂度:O(M*N),遍历整个矩阵。空间复杂度:O(1),所有操作都在原地完成,没有使用额外的存储空间。
解法五:位运算,将结果存储在每个元素的左边一位
时间复杂度:O(M*N),需要遍历整个矩阵来计算。空间复杂度:O(1),所有操作都在原地完成,没有使用额外的存储空间。
在上述解法中,除了第一种解法需要和原矩阵一样的额外空间,第三种解法使用了一个数组来存储行的状态,其他方法都采取了原地算法,即在原数组上直接修改,大大节约了空间。