目录
1、冒泡排序
2、插入排序
3、选择排序
4、归并排序
5、快速排序
6、堆排序
7、计数排序
8、桶排序
9、基数排序
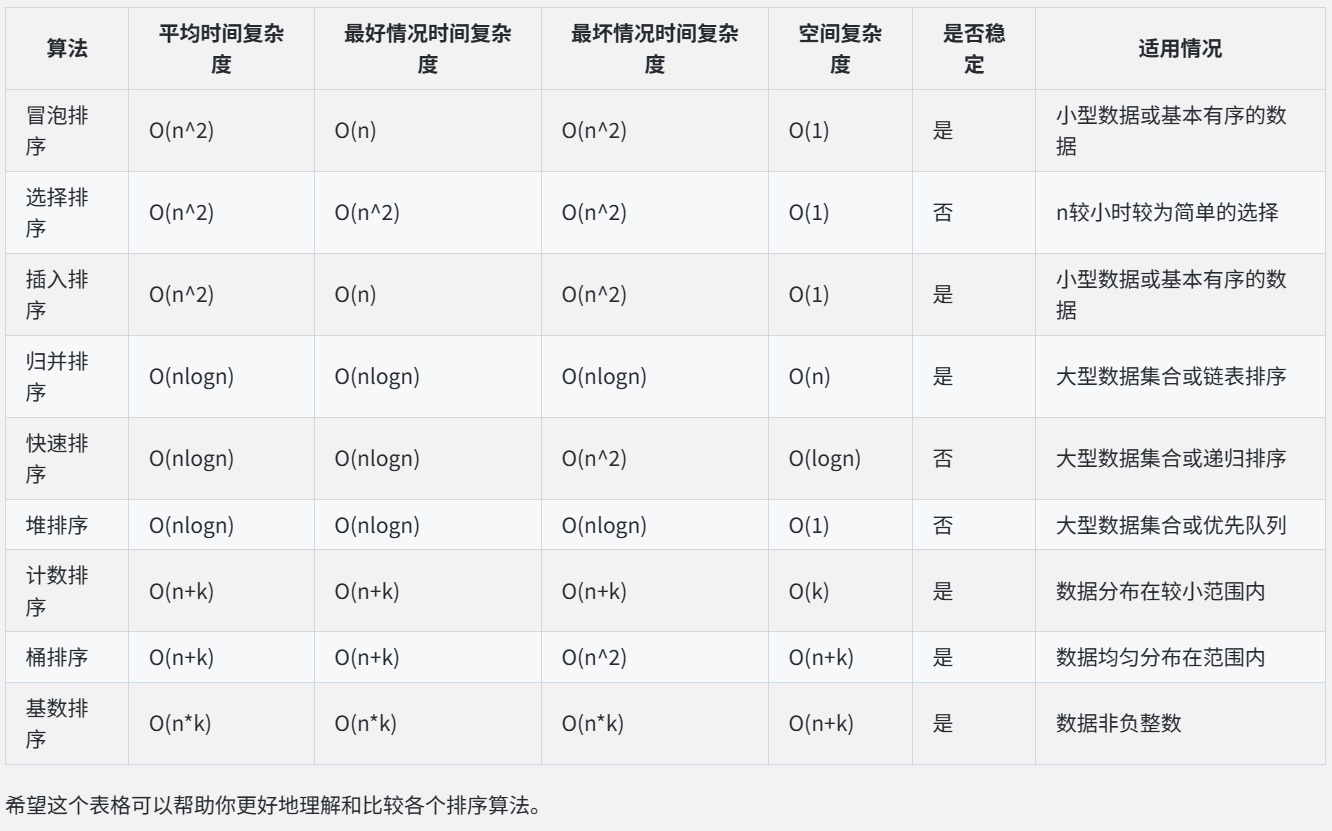
常见的排序算法包括:
- 冒泡排序(Bubble Sort)
- 插入排序(Insertion Sort)
- 选择排序(Selection Sort)
- 归并排序(Merge Sort)
- 快速排序(Quick Sort)
- 堆排序(Heap Sort)
- 计数排序(Counting Sort)
- 桶排序(Bucket Sort)
- 基数排序(Radix Sort)
1、冒泡排序
- 工作原理:
- 1、比较相邻的两个元素。如果前面的元素大于后面的元素,则交换它们的位置;
- 2、对每一对相邻的元素进行同样的操作,从开始第一对到结尾的最后一对,这样一趟比较结束后,最大的元素就"沉"到了数列的最末尾;
- 3、针对所有的元素重复以上的步骤,除了最后一个;
- 4、重复步骤1~3,当没有相邻的元素需要交换时,排序就完成了。
冒泡排序示例代码:
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {5, 2, 9, 1, 5, 6};
bubbleSort(arr);
System.out.println("\n排序后的数组:");
for (int num : arr) {
System.out.print(num + " ");
}
}
public static void bubbleSort(int[] arr) {
int n = arr.length;
boolean swapped;
for (int i = 0; i < n - 1; i++) {
swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换 arr[j] 和 arr[j + 1]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// 如果没有发生交换,说明数组已经有序
if (!swapped) {
break;
}
}
}
}
2、插入排序
- 工作原理:
- 从第一个元素开始,该元素可以认为已经被排序。
- 取出下一个元素,在已经排序的元素序列中从后向前扫描。
- 如果该元素(已排序)大于新元素,将该元素移到下一位置。
- 重复步骤 3,直到找到已排序的元素小于或等于新元素的位置。
- 将新元素插入到该位置后。
- 重复步骤 2~5,数组经过 n-1 次遍历后就会变成有序序列。
插入排序示例代码:
public class InsertionSort {
// 插入排序算法实现
public static void insertionSort(int[] array) {
int n = array.length;
// 从第二个元素开始遍历数组
for (int i = 1; i < n; i++) {
int key = array[i]; // 当前要插入的值
int j = i - 1; // 已排序部分的最后一个元素的下标
// 在已排序部分中寻找合适的位置插入key
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j]; // 向后移动元素
j--;
}
array[j + 1] = key; // 将key插入合适的位置
}
}
public static void main(String[] args) {
int[] arr = {12, 11, 13, 5, 6};
insertionSort(arr);
System.out.print("Sorted array: ");
for (int i : arr) {
System.out.print(i + " ");
}
}
}
3、选择排序
- 工作原理:
- 1、首先,从未排序的元素中找到最小(或最大)的元素。
- 2、将其放到已排序序列的末尾(或者放到另一个数组的开头)。
- 3、然后,再从剩余的未排序元素中找到最小(或最大)的元素,放到已排序序列的末尾。
- 4、重复步骤 2 和步骤 3,直到所有元素都已排序。
选择排序的伪代码:
function selectionSort(array)
n = array.length
for i from 0 to n-1
minIndex = i
for j from i+1 to n-1
if array[j] < array[minIndex]
minIndex = j
swap array[i] and array[minIndex]
end for
end function
//外层循环遍历数组,
//内层循环找到未排序部分中的最小元素,并将其与当前外层循环位置的元素交换,
//这样就不断地将最小元素放到已排序部分的末尾,直到整个数组都排序完成4、归并排序
工作原理:
分解:将待排序的数组不断地二分,直到每个子序列只有一个元素为止。
排序:对每个子序列进行排序,可以采用递归的方式来实现。
合并:将排好序的子序列再合并为一个整体有序的数组。
归并排序示例代码:
public class MergeSort {
// 归并排序的主函数,对数组array进行归并排序
public static void mergeSort(int[] array, int left, int right) {
if (left < right) {
// 计算中间位置
int middle = (left + right) / 2;
// 递归地对左半部分进行归并排序
mergeSort(array, left, middle);
// 递归地对右半部分进行归并排序
mergeSort(array, middle + 1, right);
// 合并左右两部分
merge(array, left, middle, right);
}
}
// 将两个已经排序的数组段 array[left...middle] 和 array[middle+1...right] 合并成一个有序数组
public static void merge(int[] array, int left, int middle, int right) {
// 计算左右两部分数组段的长度
int n1 = middle - left + 1;
int n2 = right - middle;
// 创建临时数组存储左右两部分的数据
int[] leftArray = new int[n1];
int[] rightArray = new int[n2];
// 将数据拷贝到临时数组
for (int i = 0; i < n1; i++) {
leftArray[i] = array[left + i];
}
for (int i = 0; i < n2; i++) {
rightArray[i] = array[middle + i + 1];
}
// 合并左右两部分数组段
int i = 0, j = 0;
int k = left;
while (i < n1 && j < n2) {
if (leftArray[i] <= rightArray[j]) {
array[k] = leftArray[i];
i++;
} else {
array[k] = rightArray[j];
j++;
}
k++;
}
// 将剩余的元素拷贝到数组中
while (i < n1) {
array[k] = leftArray[i];
i++;
k++;
}
while (j < n2) {
array[k] = rightArray[j];
j++;
k++;
}
}
}
5、快速排序
工作原理:
- 选取一个基准元素(通常选择第一个元素),将序列分割为两个子序列;
- 将小于基准的元素放在基准的左边,大于基准的元素放在右边;
- 对左右子序列分别进行递归快速排序;
- 合并左右子序列。
快速排序的示例代码:
public class QuickSort {
public static void main(String[] args) {
int[] arr = {5, 2, 9, 3, 7, 6, 1, 8, 4};
quickSort(arr, 0, arr.length - 1); // 调用快速排序算法
for (int i : arr) {
System.out.print(i + " "); // 输出排序后的数组
}
}
public static void quickSort(int[] arr, int low, int high) {
if (arr == null || arr.length == 0 || low >= high) {
return; // 如果数组为空或者low大于等于high,直接返回
}
int middle = low + (high - low) / 2; // 计算中间值的索引
int pivot = arr[middle]; // 取得中间值作为基准值
int i = low, j = high; // 初始化i和j作为左右指针
while (i <= j) { // 当i小于等于j时循环
while (arr[i] < pivot) { // 在左半部分找到第一个大于等于基准值的元素
i++;
}
while (arr[j] > pivot) { // 在右半部分找到第一个小于等于基准值的元素
j--;
}
if (i <= j) { // 如果左指针小于等于右指针
int temp = arr[i]; // 交换arr[i]和arr[j]
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
if (low < j) { // 递归处理左半部分
quickSort(arr, low, j);
}
if (high > i) { // 递归处理右半部分
quickSort(arr, i, high);
}
}
}
6、堆排序
工作原理:
构建堆:首先将待排序的数据构建成一个二叉堆,可以是最大堆或最小堆。这个步骤可以使用从下往上的循环方式,从最后一个非叶子节点开始,逐个向前调整节点使得以当前节点为根的子树满足堆的性质。
排序:将堆顶元素(最大值或最小值)与堆的最后一个元素交换位置,并将堆的大小减一。接着调整交换后的堆,使其满足堆的性质。重复以上步骤,直到整个数组排序完成。
堆排序的示例代码:
- 统计每个元素出现的次数:遍历待排序的数组,统计每个元素出现的次数,可以使用额外的辅助数组来保存计数结果。
- 根据元素的计数信息,确定元素在排序后的位置:根据元素值和它在计数数组中的计数位置,确定元素在排序后的位置。
- 将元素放置到正确的位置上:遍历待排序的数组,根据元素值在计数数组中的位置,将元素放置到正确的位置上。
- 输出排序后的结果:将排序后的元素依次输出,即得到排好序的数组。
public class HeapSort {
// 堆排序的主要入口方法,用于对整个数组进行排序
public static void sort(int[] arr) {
// 构建最大堆
buildMaxHeap(arr);
// 从最后一个非叶子节点开始,依次将根节点与末尾元素交换,并重新调整堆
for (int i = arr.length - 1; i > 0; i--) {
swap(arr, 0, i); // 将根节点与末尾元素交换
adjustHeap(arr, 0, i); // 重新调整堆
}
}
// 构建最大堆的方法
private static void buildMaxHeap(int[] arr) {
int lastIndex = arr.length - 1;
int parentIndex = (lastIndex - 1) / 2; // 最后一个非叶子节点的下标
for (int i = parentIndex; i >= 0; i--) {
adjustHeap(arr, i, arr.length);
}
}
// 调整堆的方法,使其满足最大堆的性质
private static void adjustHeap(int[] arr, int index, int length) {
int temp = arr[index]; // 当前父节点
for (int k = 2 * index + 1; k < length; k = 2 * k + 1) { // 从index结点的左子结点开始,也就是2*index+1处开始
if (k + 1 < length && arr[k] < arr[k + 1]) { // 如果左子结点小于右子结点,k指向右子结点
k++;
}
if (arr[k] > temp) { // 如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[index] = arr[k];
index = k;
} else {
break;
}
}
arr[index] = temp; // 将temp值放到最终的位置
}
// 交换数组中两个元素的方法
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 测试方法
public static void main(String[] args) {
int[] arr = {4, 6, 8, 5, 9, 1, 2, 3, 7};
sort(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
7、计数排序
工作原理:
- 统计每个元素出现的次数:遍历待排序的数组,统计每个元素出现的次数,可以使用额外的辅助数组来保存计数结果。
- 根据元素的计数信息,确定元素在排序后的位置:根据元素值和它在计数数组中的计数位置,确定元素在排序后的位置。
- 将元素放置到正确的位置上:遍历待排序的数组,根据元素值在计数数组中的位置,将元素放置到正确的位置上。
- 输出排序后的结果:将排序后的元素依次输出,即得到排好序的数组。
计数排序的示例代码:
public class CountingSortExample {
public static void countingSort(int[] array, int max) {
int[] count = new int[max + 1]; // 创建计数数组,并初始化为 0
for (int num : array) {
count[num]++; // 统计每个元素的个数
}
int k = 0;
for (int i = 0; i < count.length; i++) {
while (count[i] > 0) {
array[k] = i; // 将计数数组中的元素按顺序填充到原始数组中
k++;
count[i]--;
}
}
}
public static void main(String[] args) {
int[] array = {4, 2, 2, 8, 3, 3, 1};
int max = 8; // 数组中的最大值
System.out.println("Before sorting: " + Arrays.toString(array));
countingSort(array, max);
System.out.println("After sorting: " + Arrays.toString(array));
}
}
8、桶排序
工作原理:
- 遍历待排序数组,根据预设的规则将元素分配到对应的桶中。
- 对每个桶内的元素进行排序,可以选择使用插入排序、快速排序等方法。
- 将各个桶中的元素按顺序合并起来,得到最终的有序数组。
import java.util.ArrayList;
import java.util.Collections;
public class BucketSort {
public static void bucketSort(int[] nums) {
int bucketSize = 5; // 设置桶的大小
int maxValue = Integer.MIN_VALUE;
int minValue = Integer.MAX_VALUE;
for (int num : nums) {
maxValue = Math.max(maxValue, num); // 找到待排序数组的最大值
minValue = Math.min(minValue, num); // 找到待排序数组的最小值
}
int bucketCount = (maxValue - minValue) / bucketSize + 1; // 计算桶的个数
ArrayList<ArrayList<Integer>> buckets = new ArrayList<>(bucketCount);
for (int i = 0; i < bucketCount; i++) {
buckets.add(new ArrayList<>()); // 初始化桶
}
for (int num : nums) {
int bucketIndex = (num - minValue) / bucketSize; // 计算元素应该放入的桶的索引
buckets.get(bucketIndex).add(num); // 将元素放入对应的桶中
}
int index = 0;
for (ArrayList<Integer> bucket : buckets) {
Collections.sort(bucket); // 对每个桶内的元素进行排序
for (int num : bucket) {
nums[index++] = num; // 将排序好的元素放回原数组
}
}
}
public static void main(String[] args) {
int[] arr = {29, 25, 3, 49, 9, 37, 21, 43};
bucketSort(arr);
for (int num : arr) {
System.out.print(num + " ");
}
}
}
9、基数排序
工作原理:
- 首先,将待排序的整数按照个位数的数值进行分配到 "桶" 中。
- 然后,按照个位数的顺序将桶中的数字依次取出,组成一个新的序列。
- 接着,再以十位数的数值进行分配到对应的桶中,并按顺序取出,形成新的序列。
- 最后,以此类推,直到所有位数都分配完毕,得到有序的序列。
基数排序的示例代码:
import java.util.ArrayList;
public class RadixSort {
// 获取数字的指定位数的数字
public static int getDigit(int number, int digitPlace) {
return (number / digitPlace) % 10;
}
// 基数排序函数
public static void radixSort(int[] arr) {
// 找出数组中的最大值,以确定需要多少位数
int max = arr[0];
for (int num : arr) {
if (num > max) {
max = num;
}
}
// 计算最大值的位数
int numDigits = 1;
while (max > 9) {
max /= 10;
numDigits++;
}
// 创建 10 个桶
ArrayList<ArrayList<Integer>> buckets = new ArrayList<>();
for (int i = 0; i < 10; i++) {
buckets.add(new ArrayList<>());
}
// 进行排序
for (int digit = 1; digit <= Math.pow(10, numDigits - 1); digit *= 10) {
// 将数字分配到对应的桶中
for (int num : arr) {
int digitVal = getDigit(num, digit);
buckets.get(digitVal).add(num);
}
// 从桶中取出数字,并按顺序放回原数组
int index = 0;
for (int i = 0; i < 10; i++) {
for (int num : buckets.get(i)) {
arr[index++] = num;
}
buckets.get(i).clear(); // 清空桶,以便下一轮排序使用
}
}
}
// 测试
public static void main(String[] args) {
int[] arr = {170, 45, 75, 90, 802, 24, 2, 66};
radixSort(arr);
System.out.print("排序后的数组:");
for (int num : arr) {
System.out.print(num + " ");
}
}
}
一、1023: [编程入门]选择排序
题目描述
用选择法对10个整数从小到大排序。
输入格式
输入10个无序的数字
输出格式
排序好的10个整数
样例输入
4 85 3 234 45 345 345 122 30 12
样例输出
3
4
12
30
45
85
122
234
345
345
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int[] array=new int[10];
for(int i=0;i<10;i++) {
array[i]=scanner.nextInt();
}
selectionSort(array);
}
public static void selectionSort(int[] array) {
for(int i=0;i<array.length;i++) {
int minIndex=i;
for(int j=i+1;j<array.length;j++) {//从未排序的元素中找到最小的元素
if(array[j]<array[minIndex]) {
minIndex=j;//更新最小元素的下标
}
}
//将其放到已排序序列的末尾(0到i为已排序,j到n-1为未排序)
int temp=array[i];
array[i]=array[minIndex];
array[minIndex]=temp;
}
for(int i=0;i<10;i++) {
System.out.println(array[i]);
}
}
}






![[经验] 什么是鄱阳湖旅游最主要的景点 #知识分享#知识分享](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=https%3A%2F%2Fwww.hao123rr.com%2Fzb_users%2Fupload%2F2023%2F05%2F20230519204745168450046518177.jpg&pos_id=g5Ehc0Ar)
