连续子数组的最大和
- 题目
- 思路
- 暴力解题思路
- 画出矩阵进行分析
- 确定转移方程
- DP代码
题目
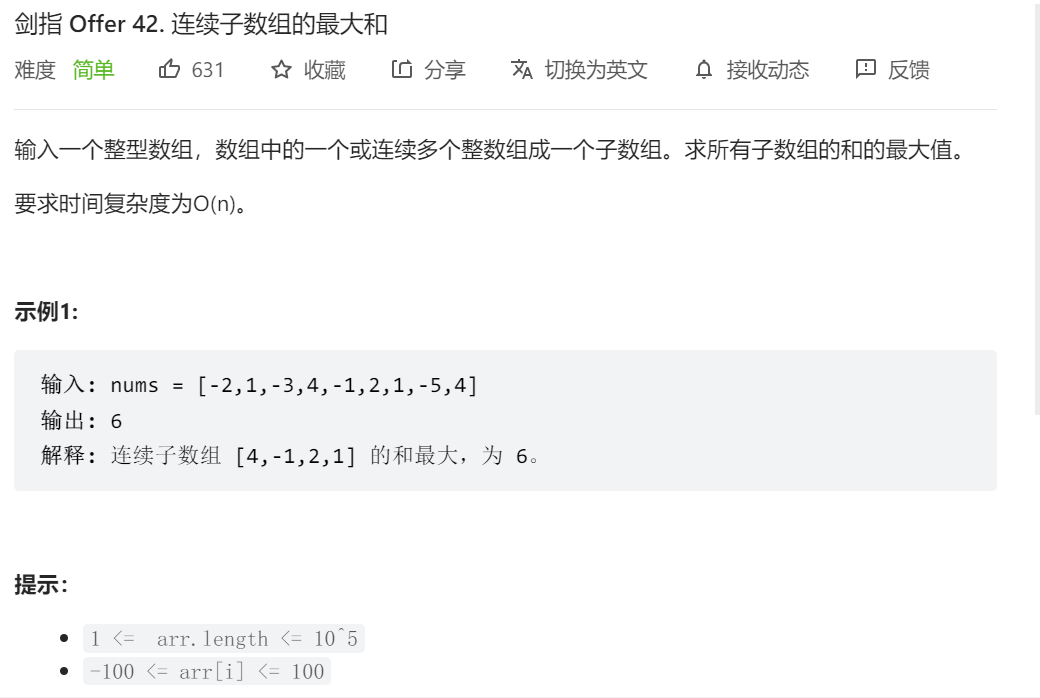
思路
从leetcode上看到的题解,突然恍然大悟,之前不容易理解转移方程终于理解了,这个思路真的对新手很友好,现在出一个C++版本,而且,我认为不应该仅仅知道最大的和多少,而且还要知道是哪个子串!

暴力解题思路
暴力的思路应该很好想,直接遍历得出所有可能的子串和,然后比较大小即可。
// O(n^2) 的暴力解法
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int main()
{
int nums[1000];
int n;
cin>>n;
for(int i=0; i<n; i++){
cin>>nums[i];
}
int mmax = INT_MIN;
for(int i=0; i<n; i++){
int sum = 0;
for(int j=i; j<n; j++){
sum += nums[j];
mmax = max(mmax,sum);
}
}
printf("最大子数列的和为:%d",mmax);
return 0;
}
上面的代码很明显,一定超时,原因在于,我们具有重复计算的数据,具体可以列出几个相关的子序列进行观察即可.
画出矩阵进行分析
在求解过程中需要计算的子数组一定如下所列,其中 s u m ( i , j ) sum(i,j) sum(i,j)代表计算从 n u m s [ i ] nums[i] nums[i]到 n u m s [ j ] nums[j] nums[j]的元素之和,我们要找到最大的 s u m ( i , j ) sum(i,j) sum(i,j)。
| ⭐ | ⭐ | ⭐ | ⭐ |
|---|---|---|---|
| sum(0,0) | |||
| sum(0,1) | sum(1,1) | ||
| sum(0,2) | sum(1,2) | sum(2,2) | |
| sum(0,3) | sum(1,3) | sum(2,3) | sum(3,3) |
| ········ | ········ | ········ | ········ |
从上面的表格我们可以看出,比如在第四行,我们在计算从 0 − 3 0-3 0−3的的范围内,哪个子数列的和最大时,比较过程如下:
- s u m ( 0 , 3 ) = n u m s [ 3 ] + n u m s [ 2 ] + n u m s [ 1 ] + n u m s [ 0 ] + 0 sum(0,3) = nums[3] + nums[2] + nums[1] + nums[0]+0 sum(0,3)=nums[3]+nums[2]+nums[1]+nums[0]+0
- s u m ( 1 , 3 ) = n u m s [ 3 ] + n u m s [ 2 ] + n u m s [ 1 ] + 0 sum(1,3) = nums[3] + nums[2] + nums[1]+0 sum(1,3)=nums[3]+nums[2]+nums[1]+0
- s u m ( 2 , 3 ) = n u m s [ 3 ] + n u m s [ 2 ] + 0 sum(2,3) = nums[3] + nums[2]+0 sum(2,3)=nums[3]+nums[2]+0
- s u m ( 3 , 3 ) = n u m s [ 3 ] + 0 sum(3,3) = nums[3] + 0 sum(3,3)=nums[3]+0
从上面的过程可以看出,每个都要加上一个 n u m s [ 3 ] nums[3] nums[3],所以,可以直接将它先不看,直接观察剩下的式子, 不正是求从 [ 0 − 2 ] [0-2] [0−2]的范围内的子数列最大的和嘛?
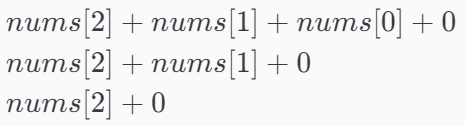
所以,我们只要每次用dp[i] 记录下来这个上一次的子数列的最大的和,不就可以在下一次计算时,就可以省略这个步骤了?
加入dp[i]之后
| ⭐ | ⭐ | ⭐ | ⭐ | 💕 |
|---|---|---|---|---|
| sum(0,0) | dp[0] | |||
| sum(0,1) | sum(1,1) | dp[1] | ||
| sum(0,2) | sum(1,2) | sum(2,2) | dp[2] | |
| sum(0,3) | sum(1,3) | sum(2,3) | sum(3,3) | dp[3] |
| ········ | ········ | ········ | ········ | dp[i] |
所以加入dp之后,再计算从0-3的最大子数列的和就可以转换为:
0-3的最大子数列的和为: n u m s [ 3 ] + d p [ 2 ] nums[3] + dp[2] nums[3]+dp[2] (当dp[2]为正数时)
- s u m ( 0 , 3 ) = n u m s [ 3 ] + n u m s [ 2 ] + n u m s [ 1 ] + n u m s [ 0 ] + 0 sum(0,3) = nums[3] + nums[2] + nums[1] + nums[0]+0 sum(0,3)=nums[3]+nums[2]+nums[1]+nums[0]+0
- s u m ( 1 , 3 ) = n u m s [ 3 ] + n u m s [ 2 ] + n u m s [ 1 ] + 0 sum(1,3) = nums[3] + nums[2] + nums[1]+0 sum(1,3)=nums[3]+nums[2]+nums[1]+0
- s u m ( 2 , 3 ) = n u m s [ 3 ] + n u m s [ 2 ] + 0 sum(2,3) = nums[3] + nums[2]+0 sum(2,3)=nums[3]+nums[2]+0
- s u m ( 3 , 3 ) = n u m s [ 3 ] + 0 sum(3,3) = nums[3] + 0 sum(3,3)=nums[3]+0
d p [ 2 ] dp[2] dp[2] 就是从0-2的最大的子数列的和,如果,前面最大的子数列和都是负数,那就没有再加上它的必要了,直接重新开始算了, d p [ 3 ] = n u m s [ 3 ] dp[3] = nums[3] dp[3]=nums[3] 因为,一个数加上一个负数,只能比它之前更小。
所以,可以确定转移方程为:
确定转移方程
d p [ j ] = { d p [ j − 1 ] + n u m s [ j ] , d p [ j − 1 ] > 0 n u m s [ j ] , d p [ j − 1 ] ≤ 0 dp[j] = \left\{\begin{array}{ll}dp[j-1]+n u m s[j], & d p[j-1]>0 \\nums[j], &dp[j-1] \leq 0\end{array}\right. dp[j]={dp[j−1]+nums[j],nums[j],dp[j−1]>0dp[j−1]≤0
所以,dp数组里面存储的就是, [ 0 − 0 ] [0-0] [0−0], [ 0 − 1 ] [0-1] [0−1], [ 0 − 2 ] [0-2] [0−2], [ 0 − 3 ] [0-3] [0−3]等范围内以 n u m s [ i ] nums[i] nums[i]为结尾的最大子数列的和,所以,最后直接遍历一边dp数组即可获得所有该该范围内的最大和。
比如:
- 当 d p [ 2 ] > 0 dp[2]>0 dp[2]>0时, d p [ 3 ] = n u m s [ 3 ] + d p [ 2 ] dp[3] = nums[3] + dp[2] dp[3]=nums[3]+dp[2];
- 当 d p [ 2 ] < 0 dp[2]<0 dp[2]<0时, d p [ 3 ] = n u m s [ 3 ] dp[3] = nums[3] dp[3]=nums[3];
都是以 n u m s [ 3 ] nums[3] nums[3]来结尾的。
| ⭐ | 💕 |
|---|---|
| 以 n u m s [ 0 ] nums[0] nums[0]结尾的最大子串和 | d p [ 0 ] dp[0] dp[0] |
| 以 n u m s [ 1 ] nums[1] nums[1]结尾的最大子串和 | d p [ 1 ] dp[1] dp[1] |
| 以 n u m s [ 2 ] nums[2] nums[2]结尾的最大子串和 | d p [ 2 ] dp[2] dp[2] |
| 以 n u m s [ 3 ] nums[3] nums[3]结尾的最大子串和 | d p [ 3 ] dp[3] dp[3] |
| 以 n u m s [ 4 ] nums[4] nums[4]结尾的最大子串和 | d p [ i ] dp[i] dp[i] |
DP代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
class Solution{
public:
//返回子序列和的最大值
int max_sum(vector<int> nums){
vector<int> dp = result_dp(nums);
int n = nums.size();
int maxx = INT_MIN;
for (int i = 0; i < n; i++)
{
maxx = max(maxx,dp[i]);
}
return maxx;
}
// 返回子序列
string max_list(vector<int> nums){
int r;
vector<int> dp = result_dp(nums);
int n = nums.size();
int maxx = INT_MIN;
for (int i = 0; i < n; i++)
{
if(maxx<dp[i]){
r = i;
maxx = dp[i];
}
}
int l = 0;
l = r;
int sum = 0;
int maxsum = max_sum(nums);
while(1)
{
sum += nums[l];
if(sum==maxsum){break;}
l--;
}
string ans="";
for(int i=l; i<=r; i++){
ans = ans + ' ' + to_string(nums[i]);
}
return ans;
}
private:
vector<int> result_dp(vector<int> nums){
int n = nums.size();
vector<int> dp(n,0);
dp[0] = nums[0];
for(int i=1; i<n; i++){
if(dp[i-1]>0){
dp[i] = dp[i-1] + nums[i];
}
else{
dp[i] = nums[i];
}
}
return dp;
}
};
void Init(vector<int>& nums)
{
for(int i=0; i<nums.size(); i++){
cin>>nums[i];
}
}
int main()
{
int n;
cin>>n;
vector<int> nums(n);
Init(nums);
Solution solu;
int mmax = solu.max_sum(nums);
string ans = solu.max_list(nums);
printf("最大子数列的和为:%d\n",mmax);
cout<<"子数列为:"<<ans;
return 0;
}