java数据结构与算法刷题目录（剑指Offer、LeetCode、ACM）-----主目录-----持续更新(进不去说明我没写完)：https://blog.csdn.net/grd_java/article/details/123063846

解题思路：时间复杂度和空间复杂度都是O(n)

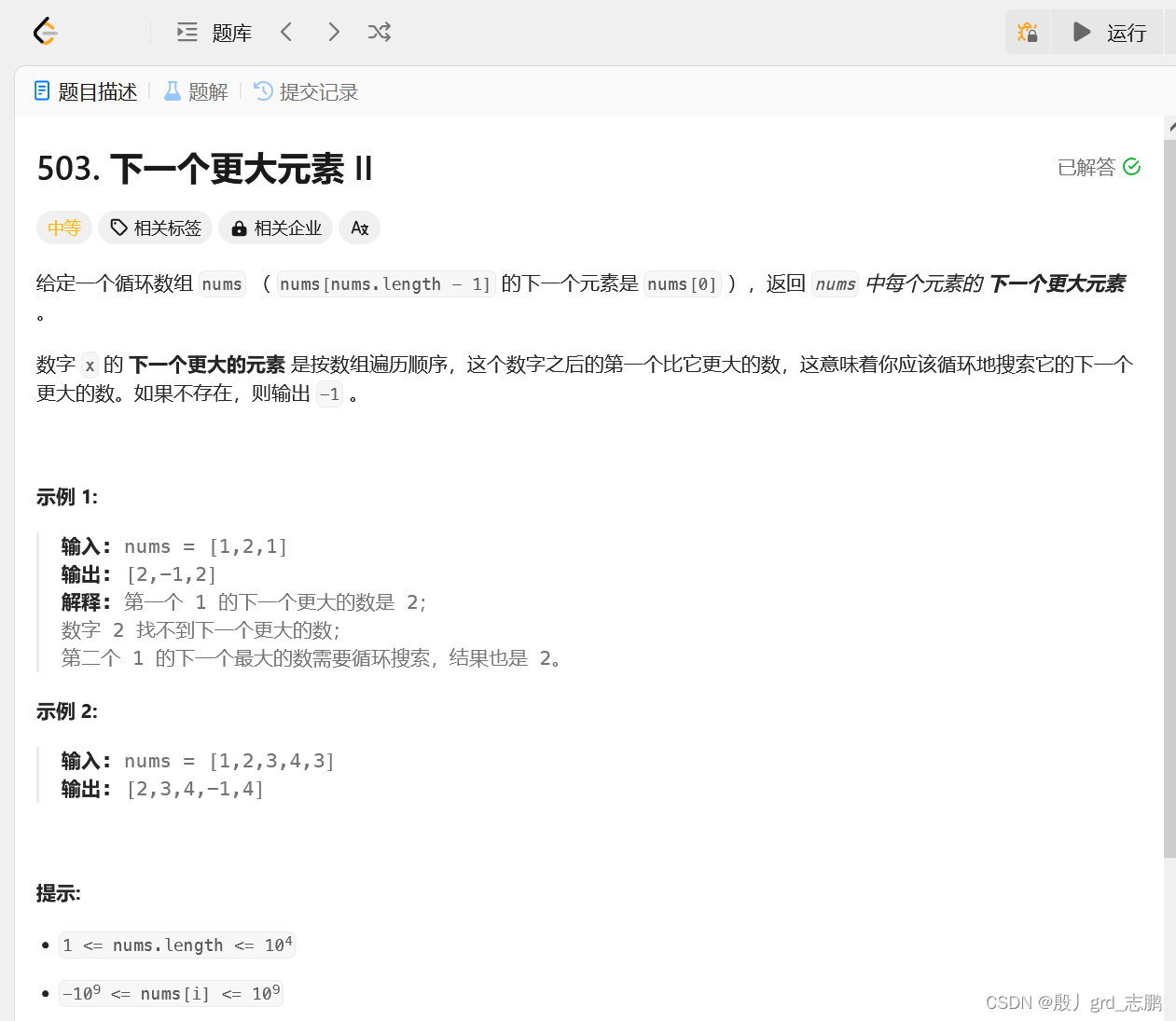
1. 此题是739题的衍生题，只不过本题将普通数组换成的循环数组。

🏆LeetCode739. 每日温度https://blog.csdn.net/grd_java/article/details/136178082

2. 则本题关键点在于如何处理循环数组

1. 首先，如果要找到每个元素的下一个比它大的，一旦需要循环找数字，那么循环后如果再次遍历到自己本身，就相当于整个数组没有比它大的元素了。
2. 所以整体只需要遍历两遍数组，那么循环数组下标的固定套路就是，当前下标%数组长度。

代码：如果想要追求超越100%的用户，可以将栈换为数组来实现。代码也会在底下给出

1. 直接用栈，不用数组实现
   

class Solution {
    //i % n 也就是当前下标取余数组长度。循环数组获取元素的固定套路。
    //例如长度为10的循环数组。我们要取下标为100的元素，那么它所指向的元素应该是100%10 = 0号
    //也就是100下标指向nums[0] 
    public int[] nextGreaterElements(int[] nums) {
        int n = nums.length;//获取数组长度
        int[] ret = new int[n];//答案数组
        Arrays.fill(ret, -1);//初始全部填充-1
        Deque<Integer> stack = new LinkedList<Integer>();//单调栈
        for (int i = 0; i < n * 2 - 1; i++) {//循环数组，所以我们遍历两遍数组
            //如果栈不为空，并且栈顶元素 < 当前遍历元素，说明我们找到了比栈顶元素大的那个
            while (!stack.isEmpty() && nums[stack.peek()] < nums[i % n]) {
                //栈顶元素出栈后，ret答案数组，保存这个栈顶元素的下一个比它大的值nums[i%n]
                ret[stack.pop()] = nums[i % n];
            }
            stack.push(i % n);//栈中存放当前元素的下标
        }
        return ret;
    }
}

2. 用数组实现：原理是完全一样的，只不过用数组来实现栈，需要更多的代码，但是数组只要初始大小设计好，不用扩容的话。存取效率要高于栈。
   

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int len = nums.length;
        int[] stack = new int[len];
        int index = -1;
        int[] res = new int[len];
        Arrays.fill(res,-1);
        for(int i=0; i<len; i++){
            int val = nums[i];
            while(index>=0 && nums[stack[index]] < val){
                res[stack[index--]] = val;
            }
            stack[++index] = i;
        }
        for(int i=0; i<len; i++){
            int val = nums[i];
            while(nums[stack[index]] < val){
                res[stack[index--]] = val;
            }
        }
        return res;
    }
}