直接上代码

import numpy as np
def fit_ellipse(points:np.array = None, extension_ratio: float = 0.2, eccentricity: float = 0.8, n_points: int = 100):
    center = np.mean(points, axis=0)
    if points.shape[0] == 2:
        axis_vector = points[1] - points[0]
        distance = np.linalg.norm(axis_vector)
        c = distance / 2 * (1 +extension_ratio)
    elif points.shape[0] == 3:
        radius = np.linalg.norm(points - center, axis=1)
        max_radius_index = np.argmax(radius)
        axis_vector = points[max_radius_index] - center
        c = np.max(radius) * (1 + extension_ratio)
    a = c / eccentricity
    b = np.sqrt(a**2-c**2)
    rotation_angle = np.arctan2(axis_vector[1], axis_vector[0])
    theta = np.linspace(0, 2*np.pi, n_points)
    dx = a * np.cos(theta)
    dy = b * np.sin(theta)
    x_rotated = dx * np.cos(rotation_angle) - dy * np.sin(rotation_angle) + center[0]
    y_rotated = dx * np.sin(rotation_angle) + dy * np.cos(rotation_angle) + center[1]
    return np.column_stack((x_rotated, y_rotated))

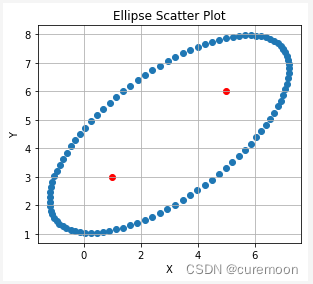
两个点的情况

points = np.array([[1,3],[5,6]])
ellipse_points = fit_ellipse(points, extension_ratio = 0.8, eccentricity=0.9)
plt.scatter(ellipse_points[:, 0], ellipse_points[:, 1])
plt.scatter(points[:, 0], points[:, 1], color='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Ellipse Scatter Plot')
plt.gca().set_aspect('equal', adjustable='box')
plt.grid(True)
plt.show()

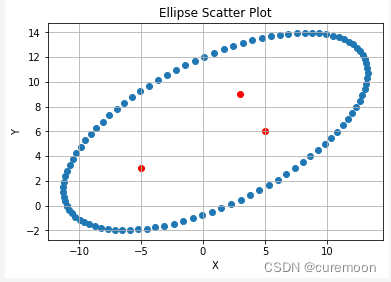
三个点的情况

points = np.array([[-5,3],[5,6],[3,9]])
ellipse_points = fit_ellipse(points, extension_ratio = 0.8, eccentricity=0.9)
plt.scatter(ellipse_points[:, 0], ellipse_points[:, 1])
plt.scatter(points[:, 0], points[:, 1], color='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Ellipse Scatter Plot')
plt.gca().set_aspect('equal', adjustable='box')
plt.grid(True)
plt.show()