关于memset和0x3f
int a[100];
memset(a,0x3f,sizeof(a) );

0x3f=0011 1111=63
C++中int型变量所占的位数为4个字节，即32位
0x3f显然不是int型变量中单个字节的最大值，应该是0x7f=0111 1111 B
那为什么要赋值0x3f：

作为无穷大使用
因为4个字节均为0x3f时，0x3f3f3f3f的十进制是1061109567，也就是10^ 9级别的（和0x7fffffff一个数量级），而一般场合下的数据都是小于10^9的，所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
可以保证无穷大加无穷大仍然不会超限。
另一方面，由于一般的数据都不会大于10^9，所以当我们把无穷大加上一个数据时，它并不会溢出（这就满足了“无穷大加一个有穷的数依然是无穷大”），事实上0x3f3f3f3f+0x3f3f3f3f=2122219134，这非常大但却没有超过32-bit int的表示范围，所以0x3f3f3f3f还满足了我们“无穷大加无穷大还是无穷大”的需求。
首先要知道memset函数是对字节为单位进行赋值的；
void *memset(void *s, int ch, size_t n);
函数解释：将s中前n个字节 （typedef unsigned int size_t ）用 ch 替换并返回 s 。
其实这里面的ch就是ascii为ch的字符；
将s所指向的某一块内存中的前n个 字节的内容全部设置为ch指定的ASCII值

最小生成树

1.最小生成树是什么
对连通图进行遍历,过程中所经过的边和顶点的组合可看做是一棵普通树,通常称为生成树。
如果连通图G的一个子图是一棵包含G的所有顶点的树，则该子图称为G的生成树(SpanningTree)。

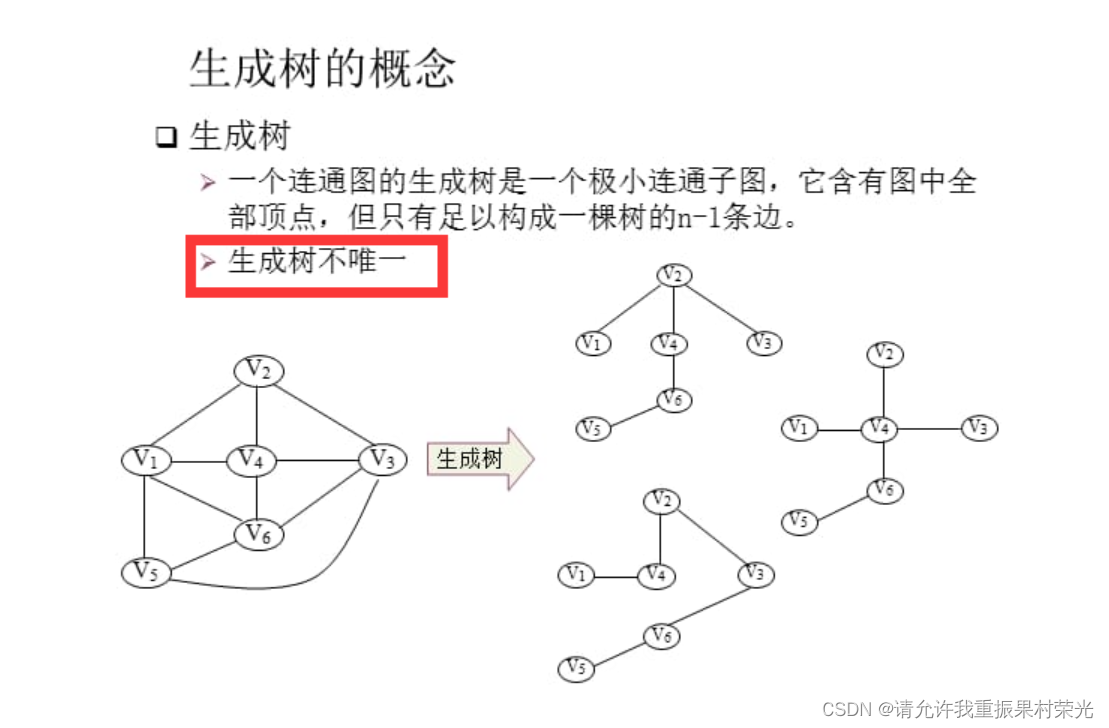
生成树是连通图的包含图中的所有顶点的极小连通子图。
图的生成树不惟一。从不同的顶点出发进行遍历，可以得到不同的生成树。
最小生成树（minimum spanning tree）其实就是一个生成树，不过它不同于一般的生成树，它的边权之和是最小的，即边权和最小的生成树。
同一个图的最小生成树也可以有很多个，但是其边权和肯定是一样的。
2.最小生成树的用途
最小生成树应用于图论知识的实际问题。生成树和最小生成树有许多重要的应用。
例如：要在n个城市之间铺设光缆，主要目标是要使这n个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

3.Prim算法描述
将图中所有顶点分为两类：树顶点（已被选入生成树的顶点）和非树顶点（还未被选入生成树的顶点）。首先选择任意一个顶点加入生成树，接下来找出一条边添加到生成树，这需要枚举每一个树顶点到每一个非树顶点所有的边，然后找到最短的边加入到生成树中。一直重复直至所有顶点都加入生成树中。
算法的具体流程如下：

从任意一个顶点（假设选1）开始构造生成树，首先将顶点1加入生成树中，用一个一维数组book标记那些顶点已经加入到了生成树中。
用数组dis记录生成树到各个顶点的距离。最初生成树只有1号顶点，有直连边时，数组dis中存储的就是1号顶点到该顶点的边的权值，没有直连边的时候就是无穷大(INT_MAX)，即初始化数组。
从数组dis中选出离生成树最近的顶点（假设为顶点j）加入到生成树中（在数组dis中的最小值）。再以j为中间点，更新生成树到每一个非树顶点的距离，如果dis[k] > e[j][k]则更新dis[k] = e[j][k]。
重复步骤3，直到生成树中有n个顶点为止。

P3366 【模板】最小生成树

最小生成树的模板题，这里用的是prim算法

证明：Prim算法之所以是正确的，主要基于一个判断：对于任意一个顶点v，连接到该顶点的所有边中的一条最短边(v, vj)必然属于最小生成树（即任意一个属于最小生成树的连通子图，从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树）

#include<bits/stdc++.h>
using namespace std;
struct node{
	int v,w;
};
vector<node>g[5005];
int dis[5005],n,m;
bool vis[5005];
int prim(int rt){
	memset(dis,0x3f,sizeof(dis));
	dis[rt]=0;
	int sum=0;
	int cnt=0;
	for(int i=1;i<=n;i++){
		int k=0;
		for(int j=1;j<=n;j++){
			if(!vis[j]&&dis[j]<dis[k]){
				k=j;
			}
		}
		if(k==0)break;
		vis[k]=true;
		sum+=dis[k];
		cnt++;
		for(int j=0;j<g[k].size();j++){
			int v=g[k][j].v,w=g[k][j].w;
			if(!vis[v]&&w<dis[v]){
				dis[v]=w;
			}
		}
	}
	if(cnt==n)return sum;
	else return -1;
}
int main(){
	int x,y,z;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d %d %d",&x,&y,&z);
		g[x].push_back(node{y,z});
		g[y].push_back(node{x,z});
	}
	int ans=prim(1);
	if(ans==-1)printf("orz");
	else printf("%d",ans);
	return 0;
}