上篇文章中,给出了对于模拟实现中功能的补全,本篇文章将优先介绍一个新的容器
之后引入什么是适配器,以及适配器的使用方法,再通过适配器的思想来完成对于
,
、优先级队列
_
的实现。
目录
1. deque:
1.1 什么是deque:
1.2 deque的大致原理以及其特点:
2. 适配器:
2.1 什么是适配器:
3. Stack的模拟实现:
3.1 功能实现:push、pop:
3.2 功能实现:top,size,empty:
3.3 测试:
4. queue的模拟实现:
4.1 queue的功能实现:
4.2 测试:
编辑5. priority_queue的模拟实现:
5.1 基本框架:
5.2 插入push以及向上调整函数Adjustup:
5.3 向下调整函数Adjustdown以及删除pop:
5.4 其余功能函数:
5.5 测试:
6. 仿函数:
6.1 仿函数的实现:
6.2 测试:
1. deque:
1.1 什么是deque:
在对的相关实现原理进行介绍前,首先来总结之前介绍的两种容器:
、
的优缺点:
对于,在前面对其进行模拟实现的文章中提到,可以将
看作之前数据结构中的顺序表,其特点是存储空间在物理以及逻辑上的连续性。因此,借由连续性可以得出,
的优点在于通过下标可以对空间中的内容进行随机访问。并且缓存命中较高对于其缺点,则是头部或者中间进行插入、删除元素时的效率过低,以及一次性开辟较多空间时带来的损耗
对于,同样提到,可以将其看作成带哨兵位头结点的双向循环链表,其特点是存储空间在逻辑上连续,但是在物理上不连续。因此,其优点在于任意位置的插入、删除数据时的效率,以及按需申请空间,不会造成浪费。但是由于其在物理上并不连续,因此不能使用下标来对
中的内容进行访问且缓存命中较低
不难看出,两者的优点几乎可以看作对于对于二者缺点的补充。而本部分介绍的容器,则可以看作是对于二者优点的一种结合。
1.2 deque的大致原理以及其特点:
对于,其内存管理方式采用了中控的方法,具体原理如下:
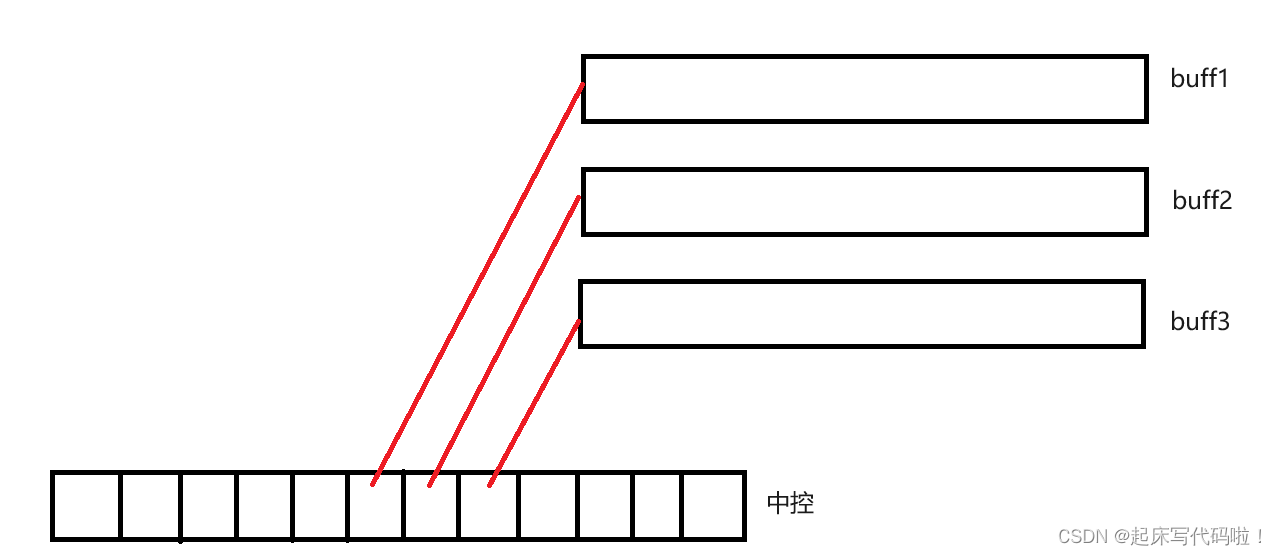
其中,中控所代表的空间是一个指针数组,里面保存了若干个指针,每个指针指向了一块空间,
对于开辟空间的大小,有相同、不同两种方式,这里采用相同进行解释,即每块空间均可以存储
个整型数据。对于上述容器,如果需要进行头插,则首先再开辟一块新的空间,这里命名为
,然后在
中插入数据即可,具体结构如下:
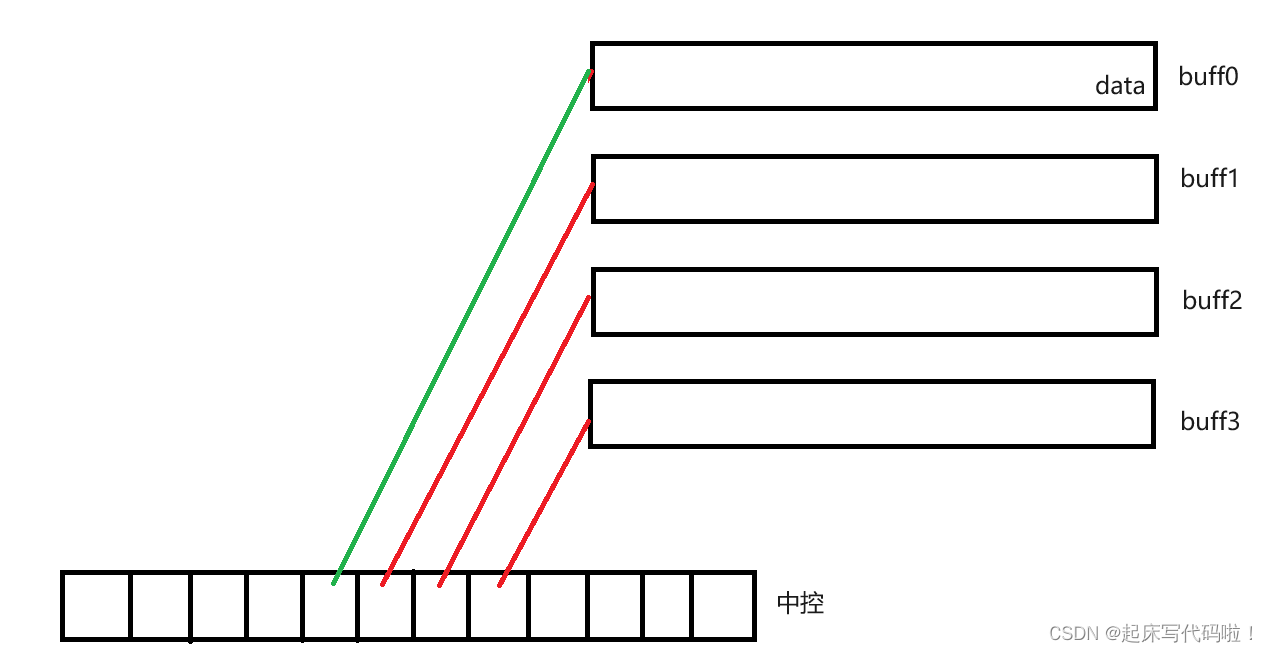
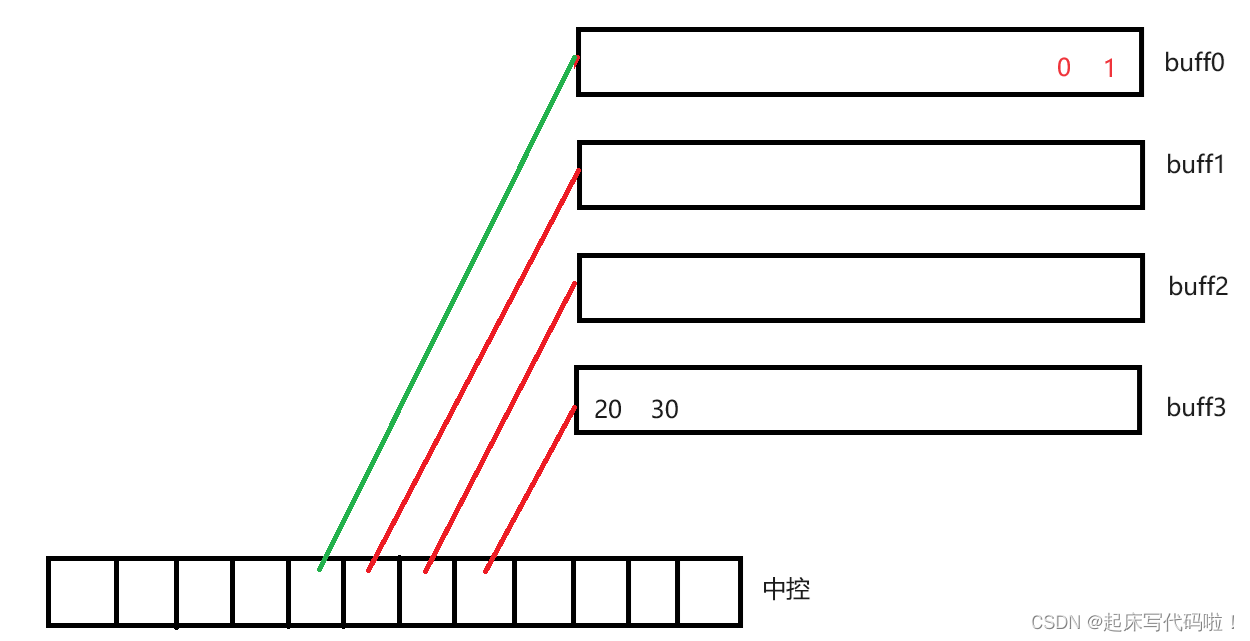
不过需要注意,进行头插时,插入数据的顺序并不是从前向后插入数据,而是从后向前依次插入数据,例如先后向
插入数据
。插入效果如下:
在对上述结构进行尾插时,只需要通过指针数组,找到最后一个,进行插入数据即可。即:
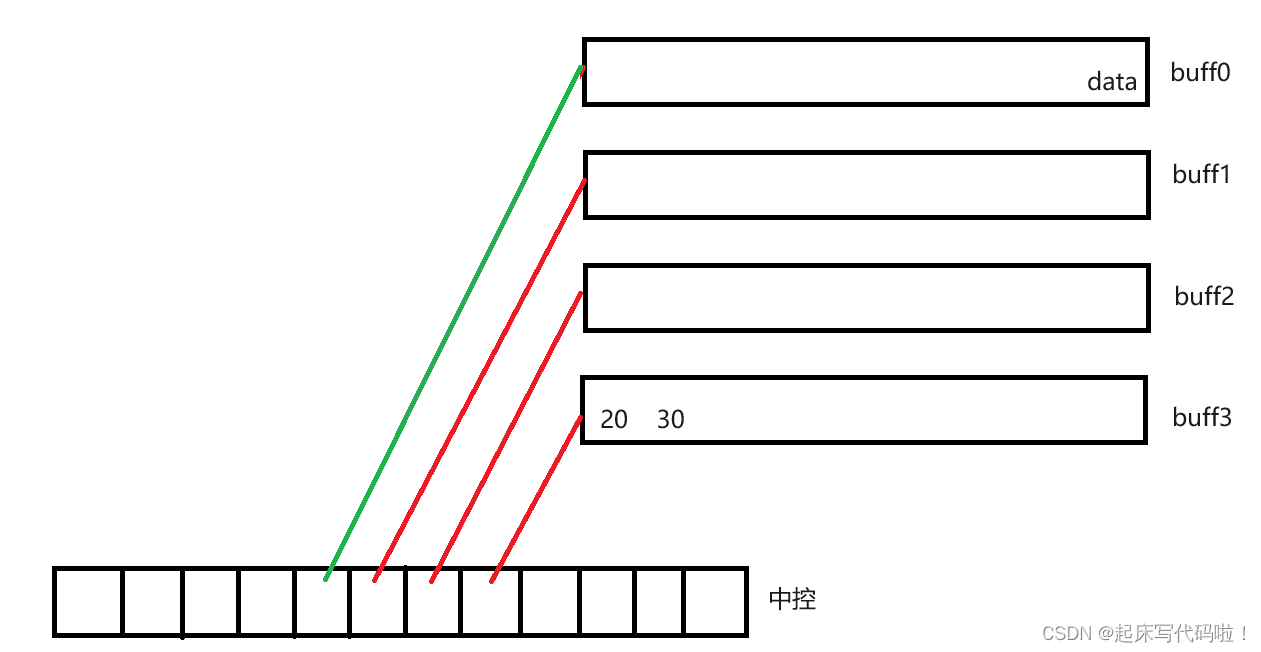
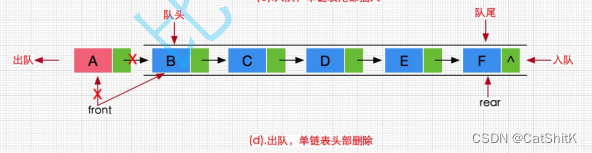
在对于进行删除数据时,例如进行头插,假设删除一个数据,效果如下:
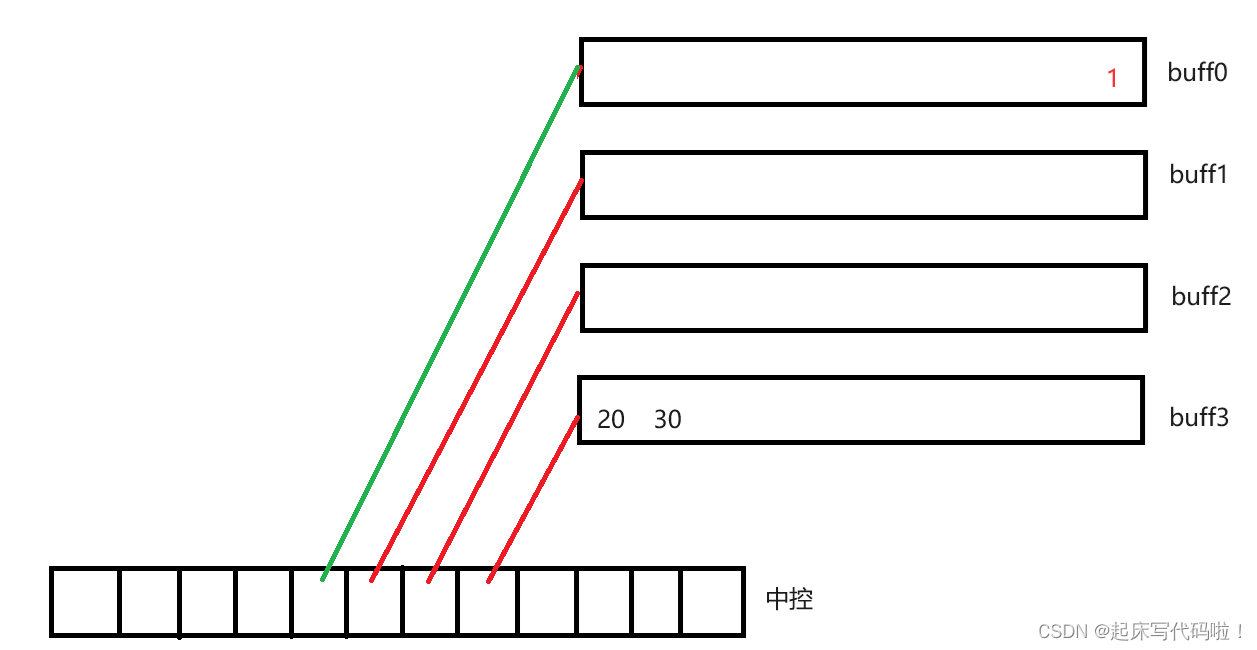
如果再删除一个数据,此时中为空,在删除数据后销毁
,效果如下:
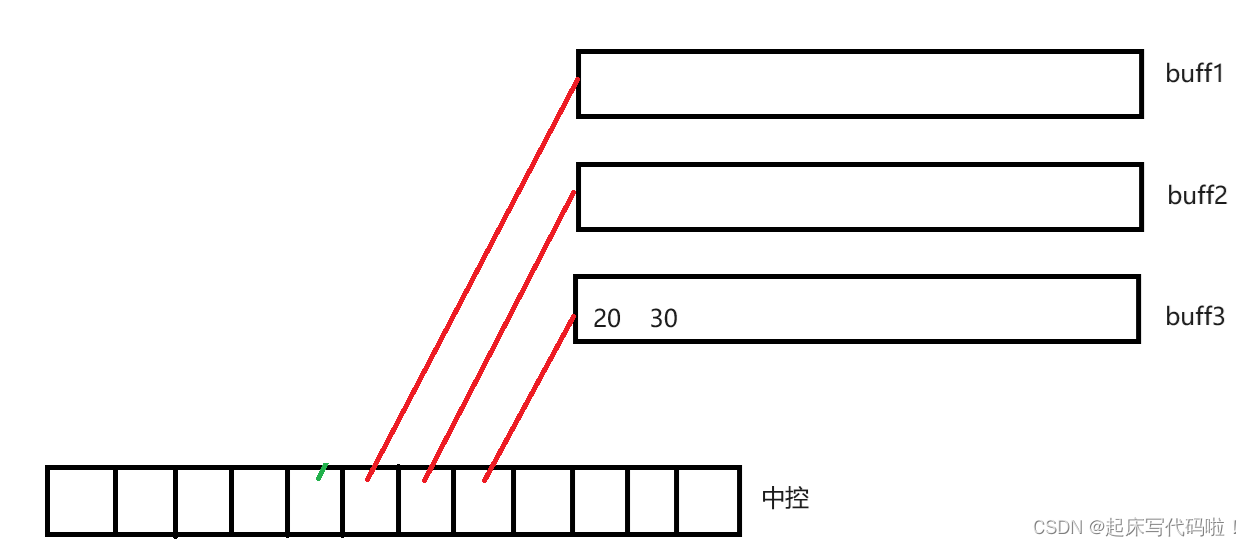
不难发现,对于,虽然其存储空间在物理上仍然保持一定的连续性,但是其头删却不会向
一样,需要进行挪动覆盖来完成。
对于的尾删,只需要找到最后一个数据所处的位置进行删除即可。
通过上述例子不难发现,对于,其头插、头删、尾插、尾删,均有着不错的效率。并且其存储空间的结构则结合了连续空间以及不连续空间。可以说是综合了
的优点,并且对二者的缺点进行了一定程度的互补。
不过,却并不能彻底代替
和
。对于
,其一大优点是可以通过下标来随意访问空间中的内容,对于
。,虽然也可以实现下标访问,但是其实现方法以及原理相对于
过于复杂。下面将对于实现原理进行简单的介绍。
假设需要利用下标访问第个位置的内容,则
可以算出需要访问的数据在第几块开辟的空间中,再利用
%
就可以计算出,需要访问的内容在空间中的具体位置。但是,如果
进行过
次头插操作,则计算时,需要先剪掉油茶数据的个数,即利用
进行后续的计算。不过需要注意,这种计算方法需要建立在每个
能存储数据的个数都是相同的。
不过,在对容器中间元素进行删除时,为了保持每个
的大小都是相同的,并不能直接对于空间进行删除,只能通过逐个挪动数据的方法来完成。这种方法与
进行头插友删时的弊端一样,效率较低。
因此,将每个的空间保持一样大,可以很好的满足下标访问功能的实现,但是,却不利于实现对于容器中间部分内容的删除以及插入。如果不限制每个存储空间的大小保持一致,有利于实现容器中间部分内容的插入以及删除,但是却不利于实现下标访问。前面矛盾。不过 ,在
库中,采取的方式是每个存储空间的大小保持一致。具体实现原理过于复杂,本文不再过多叙述。
总结不难得出,的头插,头删,尾插,尾删均有不错的效率,在接下来实现
中,将借助
来完成实现。
2. 适配器:
2.1 什么是适配器:
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。
上述给出的关于适配器的概念中提到了,适配器是一种设计模式,这种模式是将一个类的接口转换成另一个接口。例如对于上面给出的容器,可以将其看作一个接口,在对于栈和队列这两种结构的实现中,引入
这种接口,通过
中的成员函数来完成对于栈和队列的实现。对于
中的成员函数,大体如下:
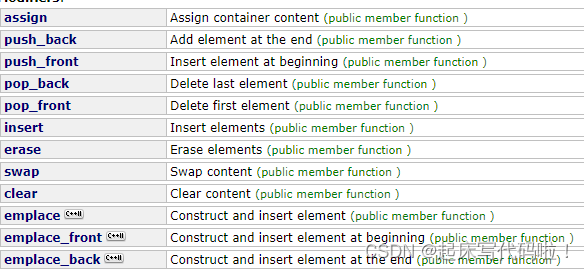
3. Stack的模拟实现:
上面说到了,可以利用适配器这种设计模式,将作为接口,来完成对于
的实现,具体原理如下:
namespace violent1
{
template<class T, class Container = deque<T>>
class Stack
{
private:
Container _con;
};
}在上述代码中,将容器作为一种模板引入,在
这个类中,通过模板参数来创建成员变量_
。此时,_
具有
的所有性质,因此,此处也不需要编写额外的构造函数来对于成员变量进行初始化。在后面对于
功能的实现中,直接调用
中的成员函数即可
3.1 功能实现:push、pop:
直接调用的成员函数即可。
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}3.2 功能实现:top,size,empty:
const T& top()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}3.3 测试:
通过下面的代码对于进行测试:
int main()
{
violent1::Stack<int> s;
s.push(1);
s.push(2);
s.push(3);
s.push(4);
while (!s.empty())
{
cout << s.top() << ' ';
s.pop();
}
return 0;
}运行结果如下: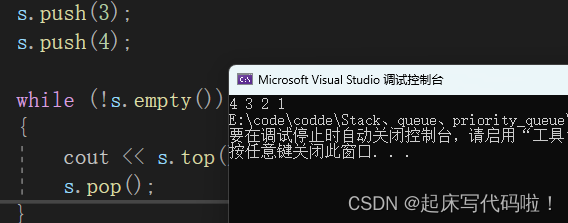
4. queue的模拟实现:
原理与实现所用的方法基本相同,只需要注意栈和队列二者本身的不同的性质即可。具体代码如下:
4.1 queue的功能实现:
namespace violent2
{
template<class T, class Container = deque<T>>
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.push_front();
}
const T& front()
{
return _con.front();
}
const T& back()
{
return _con.back();
}
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
private:
Container _con;
};
}4.2 测试:
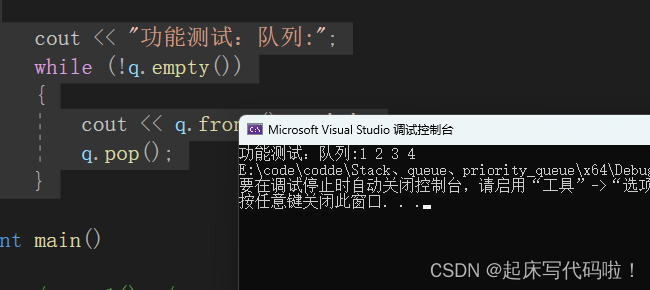
通过下面的代码对的功能进行测试:
void test2()
{
violent2::queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
cout << "功能测试:队列:";
while (!q.empty())
{
cout << q.front() << ' ';
q.pop();
}
}结果如下:
5. priority_queue的模拟实现:
5.1 基本框架:
对于_
,虽然称之为优先级队列,但是在结构上,更贴近于数据结构中的堆
(注:对于堆的介绍可以在一起学数据结构(8)——二叉树中堆的代码实现_子结点与父结交换位置-CSDN博客查看)
这里不再进行过多的叙述,只给出大体流程:
对于_
的适配器的选择,
为最佳。在插入结点时,首先插入到堆最后的叶子结点上,再利用向上调整函数
对于结点的大小关系进行调整。这里默认为实现大堆,即:任意一个父结点都大于子结点。
对于结点的删除,由于直接删除根结点可能会破坏堆的结构,因此一般选择交换最后一个叶子结点与根结点,删除此时的最后的叶子结点,利用向下调整函数对此时的根结点进行调整。
大体框架如下:
#include<iostream>
#include<vector>
using namespace std;
namespace violent3
{
template<class T, class Container = vector<T>>
class priority_queue
{
public:
private:
Container _con;
};
}5.2 插入push以及向上调整函数Adjustup:
void push(const T& x)
{
_con.push_back(x);
Adjustup(_con.size() - 1);
}
void Adjustup(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (_con[child] > _con[parent])
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}5.3 向下调整函数Adjustdown以及删除pop:
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
Adjustdown(0);
}void Adjustdown(int parent)
{
size_t child = parent * 2 + 1;
while (child < _con.size())
{
if (child + 1 < _con.size() && _con[child] < _con[child + 1])
{
child++;
}
if (_con[parent] < _con[child])
{
swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}5.4 其余功能函数:
size_t size()
{
return _con.size();
}
bool empty()
{
return _con.empty();
}
const T& Top()
{
return _con[0];
}5.5 测试:
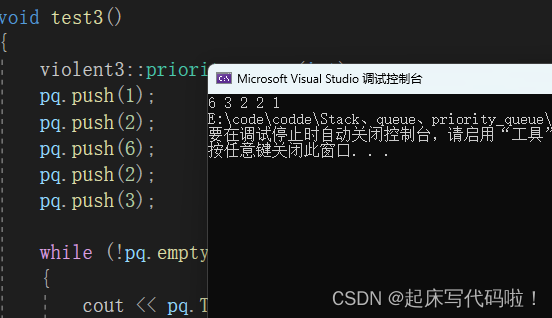
利用下面的代码对上述结构进行测试:
void test3()
{
violent3::priority_queue<int> pq;
pq.push(1);
pq.push(2);
pq.push(6);
pq.push(2);
pq.push(3);
while (!pq.empty())
{
cout << pq.Top() << ' ';
pq.pop();
}
}结果如下:
6. 仿函数:
6.1 仿函数的实现:
上面所建立的堆是大堆,如果想建立一个小堆,需要改变中的>方向,但是,针对于上方的实现方式,每次更改建立的堆的类型时,都需要对符号进行更改,过于繁琐,为了解决这个问题,引入仿函数:
对于仿函数,其并不是一个函数,而是类,例如:文章中需要用于判断建立大小堆的函数,也就是比较函数,因此,建立两个类,分别命名为即:
template<class T>
class less
{
public:
bool operator()(const T& x, const T& y)
{
return x < y;
}
};
template<class T>
class greater
{
public:
bool operator()(const T& x, const T& y)
{
return x > y;
}
};在_
的类前,将上面的类作为一个模板参数,假设在没有明确要求的情况下,默认建立大堆,则模板参数如下:
template<class T, class Container = vector<T>, class compare = greater<T>>在类中,将模板参数实例化出一个对象,这里命名为
,在需要对于父、子结点进行比较时,直接将这两个结点放入到
中,具体代码如下:
void Adjustup(int child)
{
int parent = (child - 1) / 2;
compare com;
while (child > 0)
{
if (com(_con[child], _con[parent]))
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void Adjustdown(int parent)
{
size_t child = parent * 2 + 1;
compare com;
while (child < _con.size())
{
if (child + 1 < _con.size() && com(_con[child+1],_con[child]))
{
child++;
}
if (com(_con[child],_con[parent]))
{
swap(_con[child], _con[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}6.2 测试:
利用下面的代码测试仿函数建立大堆小堆:
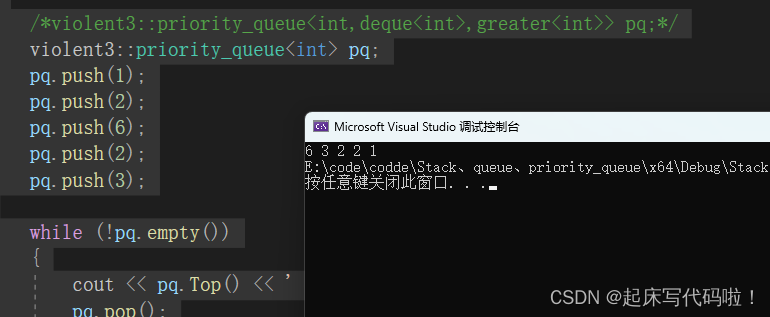
大堆:
void test3()
{
/*violent3::priority_queue<int,deque<int>,greater<int>> pq;*/
violent3::priority_queue<int> pq;
pq.push(1);
pq.push(2);
pq.push(6);
pq.push(2);
pq.push(3);
while (!pq.empty())
{
cout << pq.Top() << ' ';
pq.pop();
}
}效果如下:
小堆:
void test3()
{
violent3::priority_queue<int,deque<int>,less<int>> pq;
/*violent3::priority_queue<int> pq;*/
pq.push(1);
pq.push(2);
pq.push(6);
pq.push(2);
pq.push(3);
while (!pq.empty())
{
cout << pq.Top() << ' ';
pq.pop();
}
}效果如下: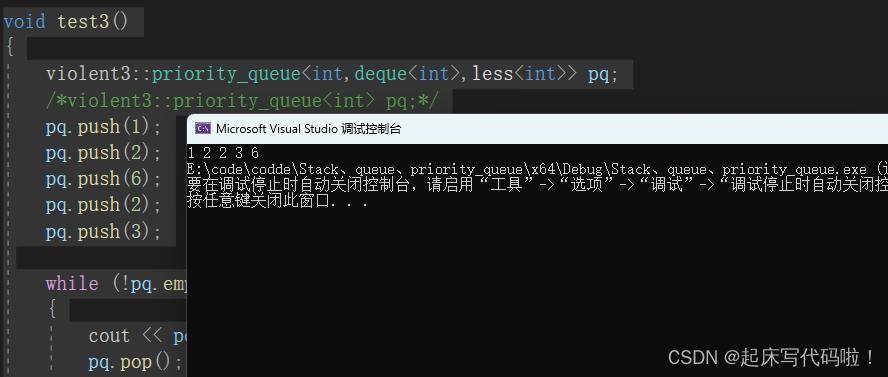




![[经验] 玄殿社区qq堂4.2 #笔记#媒体](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=https%3A%2F%2Fwww.hao123rr.com%2Fzb_users%2Fcache%2Fly_autoimg%2F%25E7%258E%2584%25E6%25AE%25BF%25E7%25A4%25BE%25E5%258C%25BAqq%25E5%25A0%25824.2.jpg&pos_id=nlcdhup0)