目录
前言
一、 32 位单精度浮点数在内存中的存储
1.1 - 符号位 sign
1.2 - 偏移后的指数位 biased exponent
1.3 - 尾数位 fraction(mantissa)
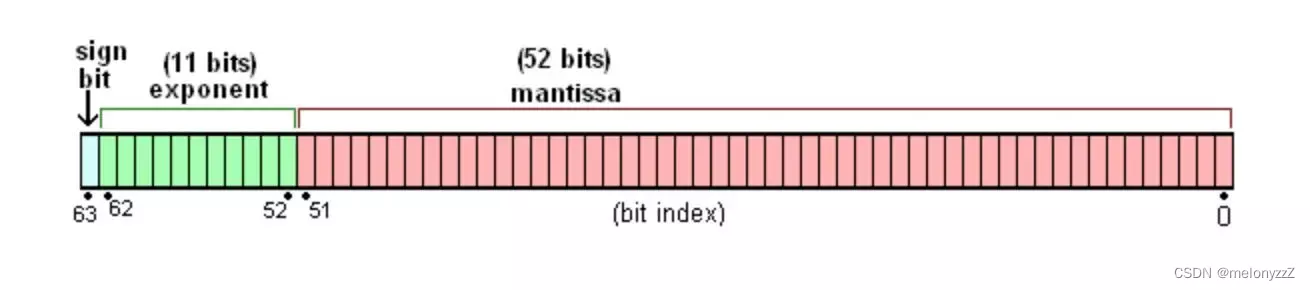
二、64 位双精度浮点数在内存中的存储
三、浮点数的比较
前言
计算机内部实际上只能存储和识别二进制,计算机中的文档、图片、数字等都是以二进制的形式存储在内存或硬盘中的。
IEEE(Institute of Electrical and Electronics Engineers,电气和电子工程师协会) 754 标准则提供了如何在计算机内存中以二进制的方式存储十进制浮点数的具体标准。
一、 32 位单精度浮点数在内存中的存储

1.1 - 符号位 sign
符号位占据最高位(第 31 位),用来表示这个浮点数是正数还是负数,其中 0 表示正数,1 则表示负数。
例如,对于十进制浮点数 5.5,其存储在内存中时,符号位应为 0,而对于十进制浮点数 -5.5,符号位则应该为 1。
1.2 - 偏移后的指数位 biased exponent
偏移后的指数位占据第 30 位到第 23 位的 8 位,用来表示以 2 为底的偏移后的指数。至于这个指数的作用,会在尾数位部分进行详解。
IEEE 754 规定,指数位用来表示 [-127, 128] 范围内的指数。不过为了表示方便,浮点数的指数位都有一个固定的偏移量(bias),使得"指数 + 偏移量 = 一个非负整数",这样指数位就不用为如何表示负数而担心了。规定:在 32 位单精度类型中,这个偏移量为 127。
1.3 - 尾数位 fraction(mantissa)
尾数位占据第 22 位到第 0 位的剩余 23 位,用来存储尾数。
以二进制方式存储十进制浮点数时:
-
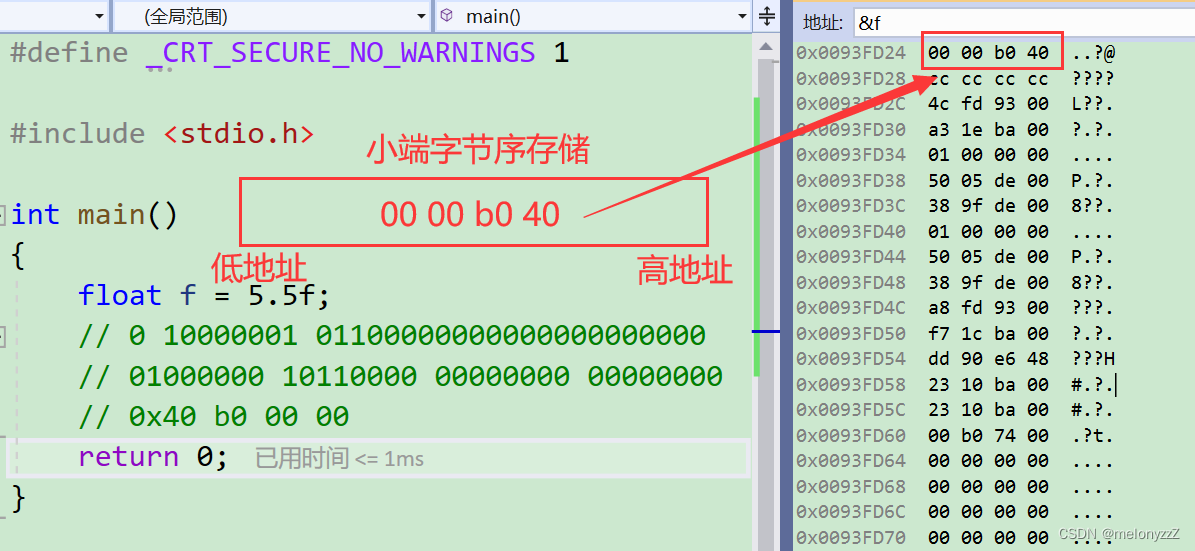
首先需要把十进制浮点数表示为二进制数。以十进制浮点数 5.5 为例:十进制浮点数 5.5 = 二进制数 101.1 -->
。
-
然后把这个二进制数表示为"尾数 * 2^指数"的形式。尾数的小数点放在第一位和第二位之间,然后保证第一位数为 1,这个处理过程叫做规范化(normalized)。
例如:101.1 = 1.011 * 2^2,其中 1.011 是尾数,指数 2 是偏移前的指数(unbiased exponent),加上偏移量后,得到的就是偏移后的指数(biased exponent) 129,它转换为二进制就是 1000 0001。
还需要对尾数进行一些特殊处理:
(1) 隐藏最高位 1:
因为尾数的最高位,即第一位始终是 1,所以在存储尾数时,可以省略第一位的 1 和小数点,只存储小数点之后的部分,这样就节约了一位内存。
所以,以后再提到尾数,如无特殊说明,指的其实是隐藏了第一位的 1 和小数点后,剩下的部分。
(2) 低位补 0:
尾数不够填满尾数位时,就需要在低位补零,补齐 23 位。因为尾数中实际上存储的是二进制中的小数部分,所以在低位补零并不影响原数值。
二、64 位双精度浮点数在内存中的存储
64 位双精度浮点数在内存中的存储大同小异。
在 64 位双精度类型中,偏移量是 1023。
三、浮点数的比较
示例:
#include <stdio.h>
int main()
{
double epsilon = 0.001; // ε
double d1 = 2.334;
double d2 = 2.335;
printf("epsilon is %lf\n", epsilon);
printf("d2 - d1 is %lf\n", d2 - d1);
if ((d2 - d1) == epsilon)
{
printf("equal\n");
}
else
{
printf("unequal\n");
}
return 0;
}程序运行后的结果:

这表明浮点数在计算机中的存储不总是精确的,所以在判断两个浮点数是否相同时,通过采用比较两数之差的绝对值是否小于一个很小的数字来确定是否相等。