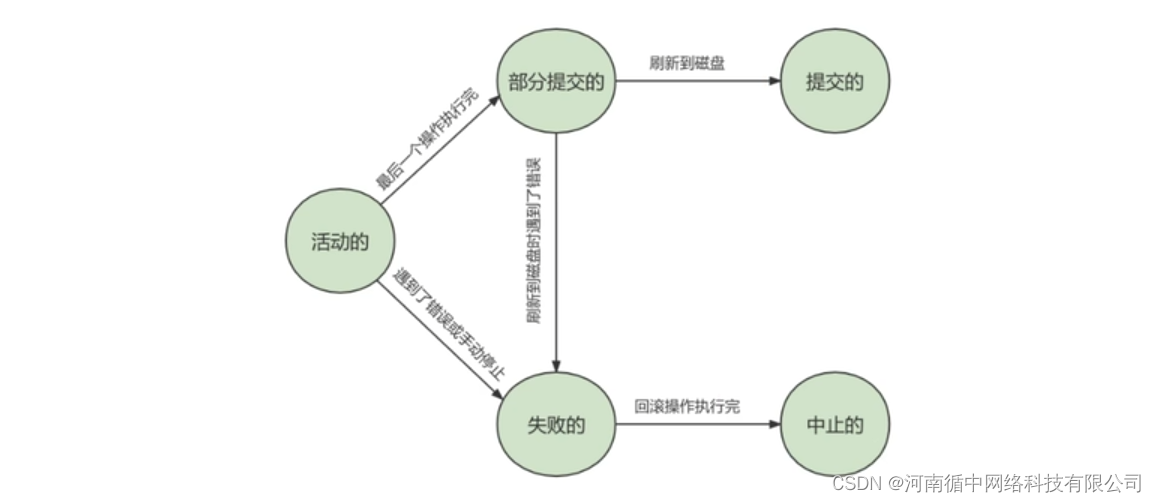
在一个m行n列的网格中,每个网格的各边的长度均相等,求由A(x1,y1)点到达B(x2,y2)点的最短路径条数,其中1<=m,n<=30。输入保证x2>=x1,y2>=y1
如有下图网格,起点和终点分别是A(1,1),B(2,3)
则最短路线是:
(1,1)->(1,2)->(1,3)->(2,3)
(1,1)->(2,1)->(2,2)->(2,3)
(1,1(->(1,2)->(2,2)->(2,3)
共3条最短路线

输入格式:
第一行输入网格的行数m和列数n
第二行输入A点的坐标
第三行输入B点的坐标
输出格式:
输出一个整数,表示从A点到达B点的最短路线条数
输入样例1:
6 7
1 1
2 3
输出样例1:
3
输入样例2:
30 30
1 1
30 30
输出样例2:
51542064最短路径条数_你也想起舞吗c的博客-CSDN博客_n乘n网格求最短路径数
//网上有很多方法,但还是这个博主的比较简洁,下面是我的一些理解
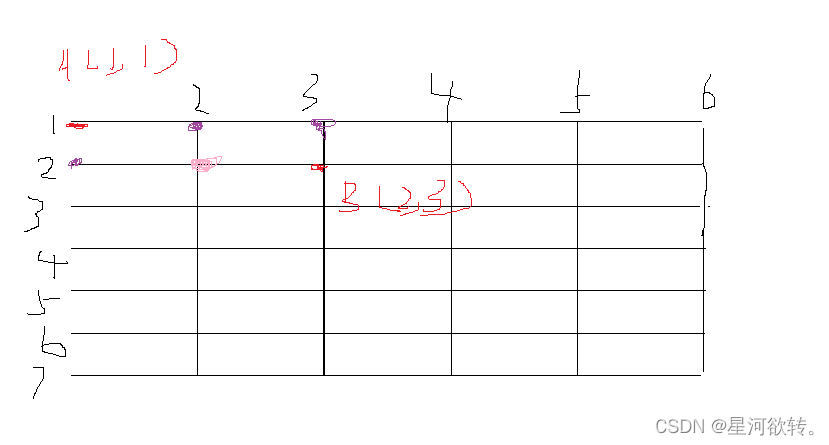
//画的图,有点丑,将就看看。我们可以把样例看成一个6*7的点阵,我们需要求A(1,1)点到B(2,3)点的最短路径条数 ,也就是图中红色点,紫色点就是我们所求条数,而其中两个紫色点可以通过粉红色的点来汇总,于是就可以把每个点设为1,然后双重循环,进行层层累加
//可能本人阐述的不清楚,大家可以自行画图或书写理解,去搞明白这个规律,然后敲代码实践
#include<bits/stdc++.h>
using namespace std;
int main()
{
int m,n, x1,y1,x2,y2, i,j,a[50][50];
for(i=0;i<50;i++)
for(j=0;j<50;j++)
a[i][j]=1;
cin>>m>>n>>x1>>y1>>x2>>y2;
for(i=x1+1;i<=x2;i++)
for(j=y1+1;j<=y2;j++)
a[i][j]=a[i-1][j]+a[i][j-1];//每一个点等于它左边点的值加上上边点的值
cout<<a[x2][y2];
return 0;
}