先回顾一下在上一篇中的内容:
聚合查询:行和行之间的数据的加工。
聚合函数:count,avg,sum......
group..by...进行分组,将指定列的值进行分组,将相同的记录合并到一个组中。每个组还可以进行聚合查询。
分组还可以指定条件进行筛选,如果是分组之前指定条件可以使用where,分组之后指定条件可以使用having。
联合查询(多表查询)和前面的单表查询相对应,主要操作是笛卡尔积。
昨天提到看了联合查询中的内连接和外连接,下面开始今天的新的内容。
一.自连接
自连接,是把自己和自己进行笛卡尔积,属于是一种比较特殊的方法,回忆一下以前的操作都是列和列之间进行的操作,但是自连接的本质是把行和行之间的比较条件转换成列和列之间。
下面我就用一个具体的例子来描述一下自连接。
先看一看数据:

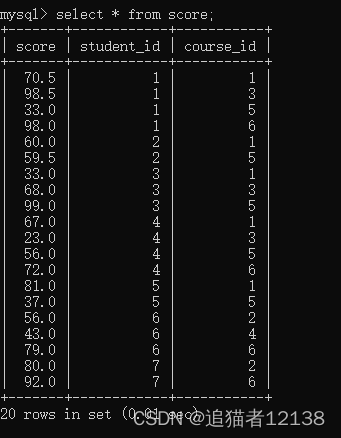
数据跟上一次的数据是一致的,就不具体展示各个table的类型了。
题目为:显示所有“计算机原理”成绩比“Java”成绩高的成绩信息
在这个问题中,可以看到,在这里的条件是按照行的方式来排列的,为了解决这个问题就需要把行给转换成列。

不确定是否可以看清楚我将代码打在下面:
select * from score as s1,score as s2 where s1.student_id=s2.student_id and s1.course_id=1 and s2.course_id=3 and s1.score<s2.score
讲一下我的思路,首先是通过自连接来使得行变成列,为了防止重名,所以将score表变成了s1和s2,之后根据数据发现我们需要把留下来的数据需要满足以来几个条件:
1.是同一个学生,所以就有了s1.student_id=s2.student_id
2.我们需要比较的是计算机原理”成绩比“Java”成绩高,所以只要保留计算机原理这门课以及java这门课,通过查询可以知道java的课程id为1,计算机原理的id为3,所以就有了s1.course_id=1 and s2.course_id=3这行代码。
3.为了满足计算机原理”成绩比“Java”成绩高,所以有了s1.score<s2.score。
4.为了精简表,之后将原代码中的*改成了s1.student_id,s1.score,s2.score。
之后修改的代码为:select s1.student_id,s1.score,s2.score from score as s1,score as s2 where s1.student_id=s2.student_id and s1.course_id=1 and s2.course_id=3 and s1.score<s2.score
二.子查询
我理解的子查询就相当于是一个套娃,子查询就是将拆分好的代码再合并到一起。
下面我们就用几个例子来简单的认识一下什么是子查询。
2.1.单行子查询
查询与“不想毕业” 同学的同班同学
一般来说我们做这个题目的思路如下:

首先我们需要知道这个同学的班级是哪个,之后需要了解这个班级里面有谁。
但是子查询的代码如下:
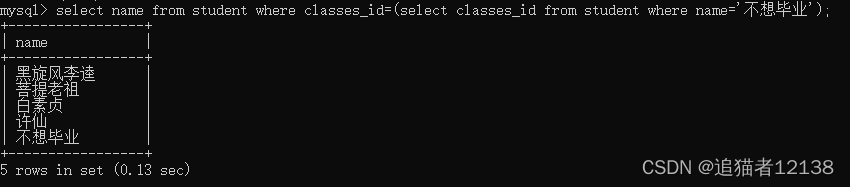
直接将两个步骤转换成了一行代码来进行编写。
这个看起来不复杂,是因为这个只是两个sql合在一起,但是当个数多了之后会发现这个是一个很复杂的工程,所以一般来说不推荐使用该操作。
2.2.多行子查询
有的时候子查询可能会查询出多条记录,就不能直接使用=,需要使用到in这样的一些操作。
下面用一个具体的例子来演示一下:
案例:查询“语文”或“英文”课程的成绩信息
按照题目要求,我们的思路应该是先找到语文和英文的课程id,之后根据课程id来找到相应的成绩信息。
下面先用简单的方法来解决一下这条题目
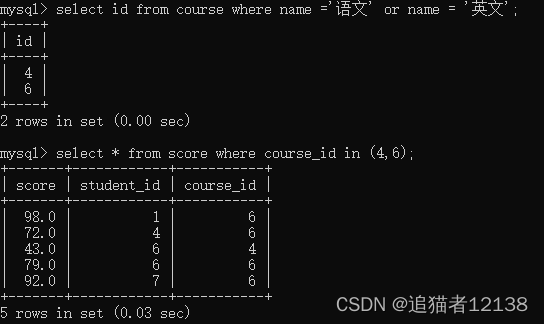
之后用子查询的的方法为:
 三.合并查询
三.合并查询
合并查询就是将多个查询语句的结果合并到一起,通过union把两个sql的查询结果合并到一起,合并的前提是两个sql查询的列是向对应的。
下面用一个例子来演示一下:
案例:查询id小于3,或者名字为“英文”的课程:

当然,这一题也可以用其他的方法来实现:

但是使用or的时候你需要保证是再通用一个表中,但是用union的时候可以不是同一个表,只要使得sql查询的列是向对应的就可以了。
当然,除了union还有一个union all,这两者的区别在于union会自动去重,但是union all不会进行自动去重。
四.MySQL的索引和事务
前面讲的sql的这些东西都是属于操作层面的,mysql的索引和事务是属于mysql原理层面的东西,面试容易考
4.1.索引
4.1.1.索引的介绍
mysql的索引其实就相当于一本书的目录当我们需要再数据库中进行查找的时候,比如说id=100,查找可以通过遍历表来实现,但是当表里面的数据特别多的时候,遍历表的操作就会比较低效。就需要尽可能的想办法避免遍历,可以通过一些特殊的数据结构,来表示一些记录的特性,通过这些特性来减少比较的次数,增加比较的效率。
索引的主要意义解释进行查找,要提高效率,但是再提高的同时,也会付出一些代价。
索引的好处:
数据库中的表、数据、索引之间的关系,类似于书架上的图书、书籍内容和书籍目录的关系。
索引所起的作用类似书籍目录,可用于快速定位、检索数据。
索引对于提高数据库的性能有很大的帮助。
索引的坏处:
占用了更多的空间
拖慢了增删改的速度
4.1.2.索引的使用场景
要考虑对数据库表的某列或某几列创建索引,需要考虑以下几点:
数据量较大,且经常对这些列进行条件查询。
该数据库表的插入操作,及对这些列的修改操作频率较低。
索引会占用额外的磁盘空间。
满足以上条件时,考虑对表中的这些字段创建索引,以提高查询效率。
反之,如果非条件查询列,或经常做插入、修改操作,或磁盘空间不足时,不考虑创建索引。
4.1.3.索引的使用
1.查看索引
show index from 表名;

直接查看student表我们会发现,里面其实已经自带了一个索引,这个自带的索引其实就是primary key 这个主键约束带来的。
所以当我们进行查询的时候,如果查询条件指定了根据主键查询,这个时候的查询速度就会很快。
unique也是带索引的。
2.创建索引
对于非主键、非唯一约束、非外键的字段,可以创建普通索引
create index 索引名 on 表名(列名);

创建索引这件事是一个非常抵消的事情,尤其是当表里面已经有很多数据的时候,在以后的工作中,如果一个表中没有索引,你不要贸然去创建索引。

通过上述操作之后我们在通过查看索引会发现,我们新创建的索引已经被添加进入了。
3. 删除索引
drop index 索引名 on 表名;

4.2.“索引背后的数据结构”
面试的时候主要考的就是索引背后的数据结构。
索引,数据结构需要的是能够加快查找的速度。
下面来简单回顾一下我学习的一些数据结构,并且进行一些简单的分析:
首先先排除顺序表还有链表:因为对于这两个表来说,他们的查找其实就是遍历,我们这边的查找是按照值去进行查找,但是在顺序表还有链表中是根据下标来进行查找的,按照下标来访问元素不叫查找。
之后我们就会想到二叉树(搜索树)一般来说二叉树的时间复杂度是logn,最坏情况下是O(N),也就是单枝树,也就是链表,而我们要做的就是不让二叉搜索树变成单枝树。
AVL:要求任意节点左右子树高度不超过1;
红黑树:要求更宽松的平衡二叉树;
但是二叉树也不太适合,二叉树最大的问题就是当元素多了之后,高度就会增加,而高度就对应着比较次数,对于数据库来说,每次比较就意味着磁盘IO
哈希表也不是很适合,虽然哈希表的搜索速度很快O(1),但是只能针对”相等“进行判定,不能对”大于小于“,以及范围查找进行判定。
堆就更不适合作为索引了,因为堆只能找最大值或者最小值。
最适合做索引的。还得是树形结构,只不过不再是二叉树,当我们使用”多叉搜索树”,高度自然也就下降了。
在数据库中使用的这个多叉搜索树又不太一样,是一个很特殊的B+树(这个是数据库索引中最常见的数据结构)
数据库有很多种,每个数据库的底层有支持多种存储引擎(实现了数据具体按照啥结构来存储的程序)每个存储引擎数据的结构可能都不一样,背后的索引结构可能也不同。
要想了解B+树,需要先理解它的前身,B树(有的资料上也写作B-树)
下面用图像来表示一下B树;
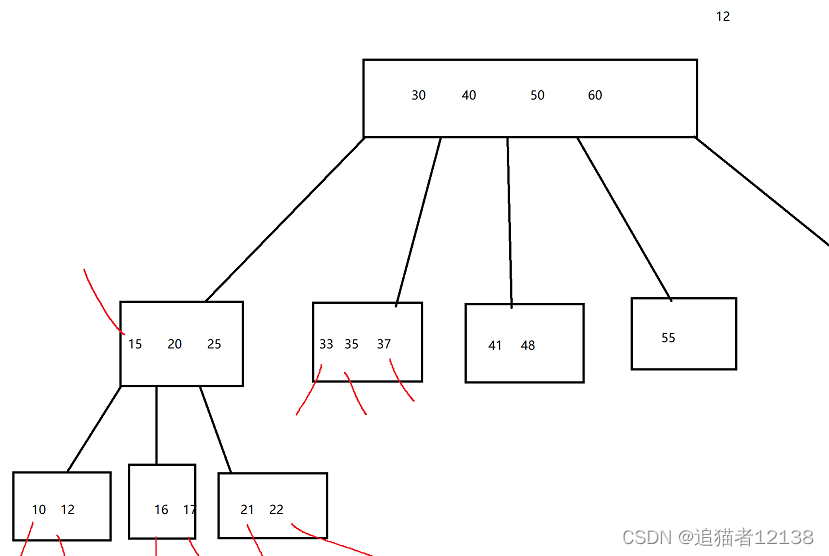
在B树里面,B树的每一个接待你,都会村粗N个key值,N个key值就划分除了N+1个区间,每个区间都对应到一个子树;在B树中查找元素,过程就和二叉搜索树非常相似,先从跟节点出发,根据待比较的元素,确定一个区间,在确定区间的时候,二叉搜索树是每个节点搜索比较一次,比较的次数和高度相关,但是B树,高度是少了,但是每个节点比较多次。相对于比较次数来说,IO次数更关键的,是以节点为单位进行磁盘IO的。
B树只是B+树的前身,B+树是在B树的基础上进行了一些更改。
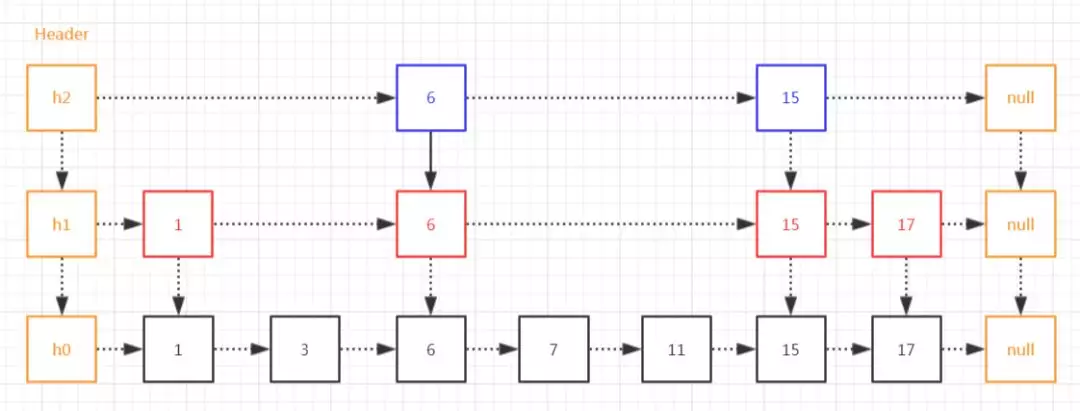
下面我用图来表达一下B+树是什么样子的。

B+树也是一个N叉搜索树,每个节点上都包含多个key值,每个节点如果又N个key,就分成N个区间,父节点的值,都会在子节点中体现,非叶子节点的每个值,最后都会在叶子节点中体现出来。父节点中的值,会作为子节点中的最大值(最小值),咱们这个图画的是最大值的情况,最下面的叶子节点,就会使用链表进行按照顺序连接。
从B树和B+树的介绍可以看出,B+树就是为了数据库索引量身打造的。
1.使用B+树进行查找的时候,整体的IO次数也会比较小
2.所有的查询到最后都会落在叶子节点上面,每次查询的IO次数都是差不多的,查询速度稳定
3.叶子节点用链表连接之后,非常适合进行范围查找
4.所有的数据存储(载荷)都是放在叶子节点上的,非叶子节点中会保存key值即可,因此非叶子节点整体占用的空间较小,甚至可以缓存到内存中