🚀 算法题 🚀

🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样✨
🌲 作者简介：硕风和炜，CSDN-Java领域优质创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯

🚀 算法题 🚀

🚩 题目链接

• 590. N 叉树的后序遍历

⛲ 题目描述

给定一个 n 叉树的根节点 root ，返回 其节点值的 后序遍历 。

n 叉树 在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例 1：

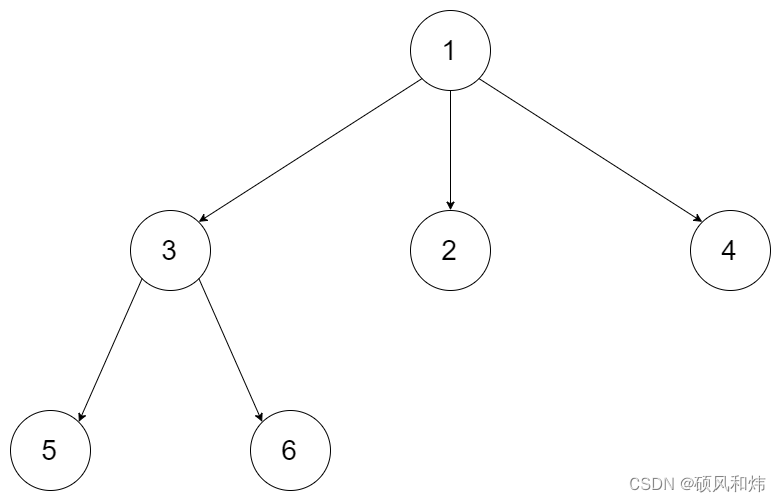
输入：root = [1,null,3,2,4,null,5,6]
输出：[5,6,3,2,4,1]
示例 2：

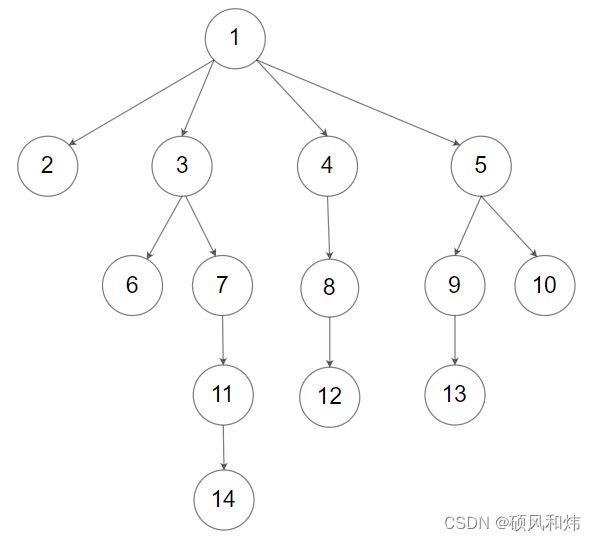
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[2,6,14,11,7,3,12,8,4,13,9,10,5,1]

提示：

节点总数在范围 [0, 104] 内
0 <= Node.val <= 104
n 叉树的高度小于或等于 1000

进阶：递归法很简单，你可以使用迭代法完成此题吗?

🌟 求解思路&实现代码&运行结果

---

⚡ DFS

🥦 求解思路

1. 该题目是二叉树后序遍历的变种，该题目是多叉树，多加一个迭代的过程即可。
2. 有了基本的思路，接下来我们就来通过代码来实现一下递归和迭代的解法。

🥦 实现代码

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/
// 递归
class Solution {

    private List<Integer> list = new ArrayList<>();

    public List<Integer> postorder(Node root) {
        dfs(root);
        return list;
    }

    public void dfs(Node root) {
        if (root == null)
            return;
        for (Node node : root.children) {
            dfs(node);
        }
        list.add(root.val);
    }
}


// 迭代:通过栈来模拟先进后出的特性
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {

    private List<Integer> list = new ArrayList<>();

    public List<Integer> postorder(Node root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }

        Deque<Node> stack = new ArrayDeque<Node>();
        stack.push(root);
        while (!stack.isEmpty()) {
            Node node = stack.pop();
            res.add(node.val);
            for (int i = 0; i <= node.children.size() - 1; i++) {
                stack.push(node.children.get(i));
            }
        }
        Collections.reverse(res);
        return res;
    }
}

🥦 运行结果

---

💬 共勉

最后，我想和大家分享一句一直激励我的座右铭，希望可以与大家共勉！