什么是单调栈
对于一个数组,需要对每个位置生成,左右两边离它最近的,比它小(或比它大)的位置在哪
例如:
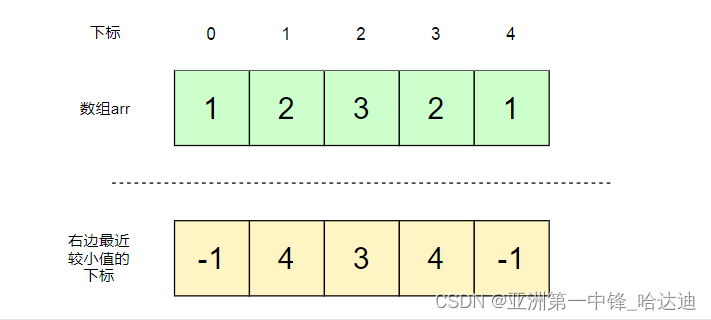
如果对每个位置都遍历下左右两边,找到第一个比它小的位置,就是O(N ^ 2)的算法
单调栈结构就是专门解决这种问题,能做到整个过程的时间复杂度为O(N)
流程
准备一个栈,栈中保存元素的下标,要求元素从从栈底到栈顶是由小到大的顺序排列
从左到右遍历整个数组arr
当遍历到一个数i时,如果arr[i]比栈顶的元素peek所代表的数arr[peek]小,此时如果将arr[i]压入栈中,就改变了栈的顺序,使得从栈底到栈顶不是由小到大,因此需要将栈顶元素peek弹出
此时位置为peek的数:
-
在它左边离它最近且比它小的数,就是现在的栈顶元素代表的数- 如果此时栈是空的,说明它左边没有比它小的数
-
在它右边离它最近且比它小的数,就是arr[i]
当遍历完整个数组后,开始清理栈中的元素,依次从栈顶弹出元素:
-
在它左边离它最近且比它小的数,就是现在的栈顶元素代表的数- 如果此时栈是空的,说明它左边没有比它小的数
-
在它右边离它最近且比它小的数:没有
这个流程为什么正确?下文有详细的正确性证明
代码如下:
public int[][] getNearestLess(int[] arr) {
int n = arr.length;
// 返回每个位置i,左边最近最小的位置:res[i][0],右边最近最小的位置:res[i][1]
int[][] res = new int[n][2];
Stack<Integer> stack = new Stack<>();
for (int i = 0;i<n;i++) {
while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
Integer pop = stack.pop();
// 收集弹出的数的答案
res[pop][0] = stack.isEmpty() ? -1 : stack.peek();
res[pop][1] = i;
}
stack.push(i);
}
// 处理栈中剩下的数
while (!stack.isEmpty()) {
Integer pop = stack.pop();
res[pop][0] = stack.isEmpty() ? -1 : stack.peek();
res[pop][1] = -1;
}
return res;
}
时间复杂度
由于在每次循环中的操作,就是让一些数进栈,出栈,每个位置最多进栈一次,出栈一次,不可能大于一次
因此整个流程耗时O(N)
正确性证明
当从栈中弹出一个元素时,为什么让它弹出的这个数,就是它右边离它最近,且比它小的数?
假设此时栈中栈顶元素为b,b下面压着a,遍历到c,且b < c
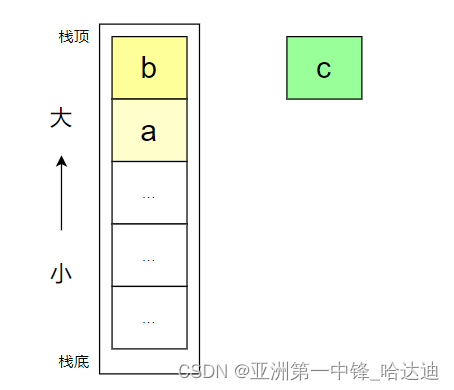
因为遍历到c时,b在栈中,因此b的下标比c的下标小,b在c的左边
b和c中间,有没有可能存在比b更小的数?

答案是不可能,因为如果存在,假设为k,那在遍历到k时,就会把b弹出,而轮不到现在c来弹出b
因此,b和c中间没有比b小的数,而现在c < b,因此c就是b右边离b最近,且比它小的数
再来证明,为什么b左边离b最近,且比它小的数为a
因为b压着a,因此在数值中,a一定在b的左边
讨论a和b之间的数,有哪些可能性

-
小于a:不可能,因为如果有,在遍历到这个数时就把a弹出了,而现在栈中还有a -
大于a,小于b:不可能:- 因为如果有这种数,这个数现在会压在a的上面,而不是b来压在a的上面。
- 当然,这个数可能在遍历到b时,就被弹出了,但使得该数弹出的数,也会压在a的上面,而不是现在b压在a的上面
无论怎样,只要a和b之间有大于a小于b的数,都不会轮到b来压在a的上面
综上所述,a和b之间只会有大于等于b的数,因此a就是b左边离b最近,且比它小的数