LeetCode 110.平衡二叉树

题目链接：110.平衡二叉树
文章讲解：代码随想录#110.平衡二叉树
视频讲解：后序遍历求高度，高度判断是否平衡 | LeetCode：110.平衡二叉树

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例1

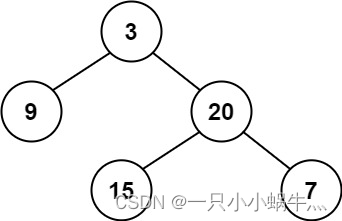
输入：root = [3,9,20,null,null,15,7]
输出：true

示例2

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例3

输入：root = []
输出：true

提示

• 树中的节点数在范围 [0, 5000] 内
• -10^4 <= Node.val <= 10^4

思路

这道题的关键是每个节点 的左右两个子树的高度差的绝对值不超过1。
可以通过后序遍历来计算每个节点的左右子树的高度（该节点到叶子节点），如果超过1说明不是平衡二叉树。
具体思路可以看代码随想录。

参考代码

int getHeight(struct TreeNode *node)
{
    if (node == NULL)
        return 0; // 当遇到空节点时终止，返回0
    
    int lcnt = getHeight(node->left); // 处理左子树
    if (lcnt == -1) // 如果左子树不是平衡二叉树，则直接返回-1
        return -1;
    int rcnt = getHeight(node->right); // 处理右子树
    if (rcnt == -1) // 如果右子树不是平衡二叉树，则直接返回-1
        return -1; 
    
    if (abs(lcnt - rcnt) > 1) { // 处理中节点
    	// 如果左右节点高度超过1，说明以中节点为根节点的二叉树不是平衡二叉树
        return -1; 
    }
    int depth = lcnt > rcnt ? lcnt : rcnt;
    return 1 + depth;

}
bool isBalanced(struct TreeNode* root) {
    if (root == NULL)
        return true;
    if (getHeight(root) == -1)
        return false;
    return true;
}

---

LeetCode 257. 二叉树的所有路径

题目链接：257. 二叉树的所有路径
文章讲解：代码随想录#257. 二叉树的所有路径
视频讲解：递归中带着回溯，你感受到了没？| LeetCode：257. 二叉树的所有路径

题目描述

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例1

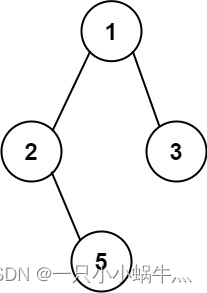
输入：root = [1,2,3,null,5]
输出：[“1->2->5”,“1->3”]

示例2

输入：root = [1]
输出：[“1”]

提示

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

思路

本题需要使用递归结合回溯对节点进行前序遍历。

参考代码

int cnt;
typedef struct {
    int index;
    int num[100];
}Stack;

void traversal(struct TreeNode *node, Stack *stack, char **res)
{
    stack->num[stack->index] = node->val; // 将中节点的数值添加到stack中
    if (node->left == NULL && node->right == NULL) { // 当遍历到叶子节点时输出
        int len = 0;
        char ch[10000] = {0};
        for (int i = 0; i <= stack->index; i++) {
            char s[5] = {0};
            sprintf(s, "%d", stack->num[i]);
            len += strlen(s);            
            strcat(ch, s);
            if (i < stack->index) {
                len += 2;
                strcat(ch, "->"); 
            }
        }
        ch[len++] = '\0';
        res[cnt] = (char*)malloc(len * sizeof(char));
        strcpy(res[cnt++], ch);
        return;
    }

    if (node->left) { // 处理左节点
        stack->index++;
        traversal(node->left, stack, res);
        stack->index--; // 回溯
    }
    if (node->right) { // 处理右节点
        stack->index++;
        traversal(node->right, stack, res);
        stack->index--; // 回溯
    }
}

char** binaryTreePaths(struct TreeNode* root, int* returnSize) {
    if (root == NULL) return NULL;
    cnt = 0;
    char **res = (char **)malloc(100*sizeof(char*));
    Stack stack = {0};
    traversal(root, &stack, res);
    *returnSize = cnt;
    return res;
}

---

LeetCode 404.左叶子之和

题目链接：404.左叶子之和
文章讲解：代码随想录#404.左叶子之和数
视频讲解：二叉树的题目中，总有一些规则让你找不到北 | LeetCode：404.左叶子之和

题目描述

给定二叉树的根节点 root ，返回所有左叶子之和。

示例1

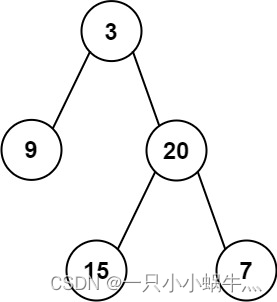
输入：root = [3,9,20,null,null,15,7]
输出：24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例2

输入：root = [1]
输出：0

提示

• 节点数在 [1, 1000] 范围内
• -1000 <= Node.val <= 1000

思路

如何确定一个节点是左叶子？
如果一个节点的左孩子节点不为空，并且左孩子节点它的左右孩子节点都为空，则这个节点的左孩子节点为左叶子节点。
也就是说，无法判断当前节点是不是左叶子，需要通过该节点的父节点来判断其父节点的左孩子是不是左叶子节点。

参考代码

int sumOfLeftLeaves(struct TreeNode* root){
    if (root == NULL) return 0;
    int val = 0;
    if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
        val = root->left->val; // 找到左叶子节点
    }
    return val + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
}