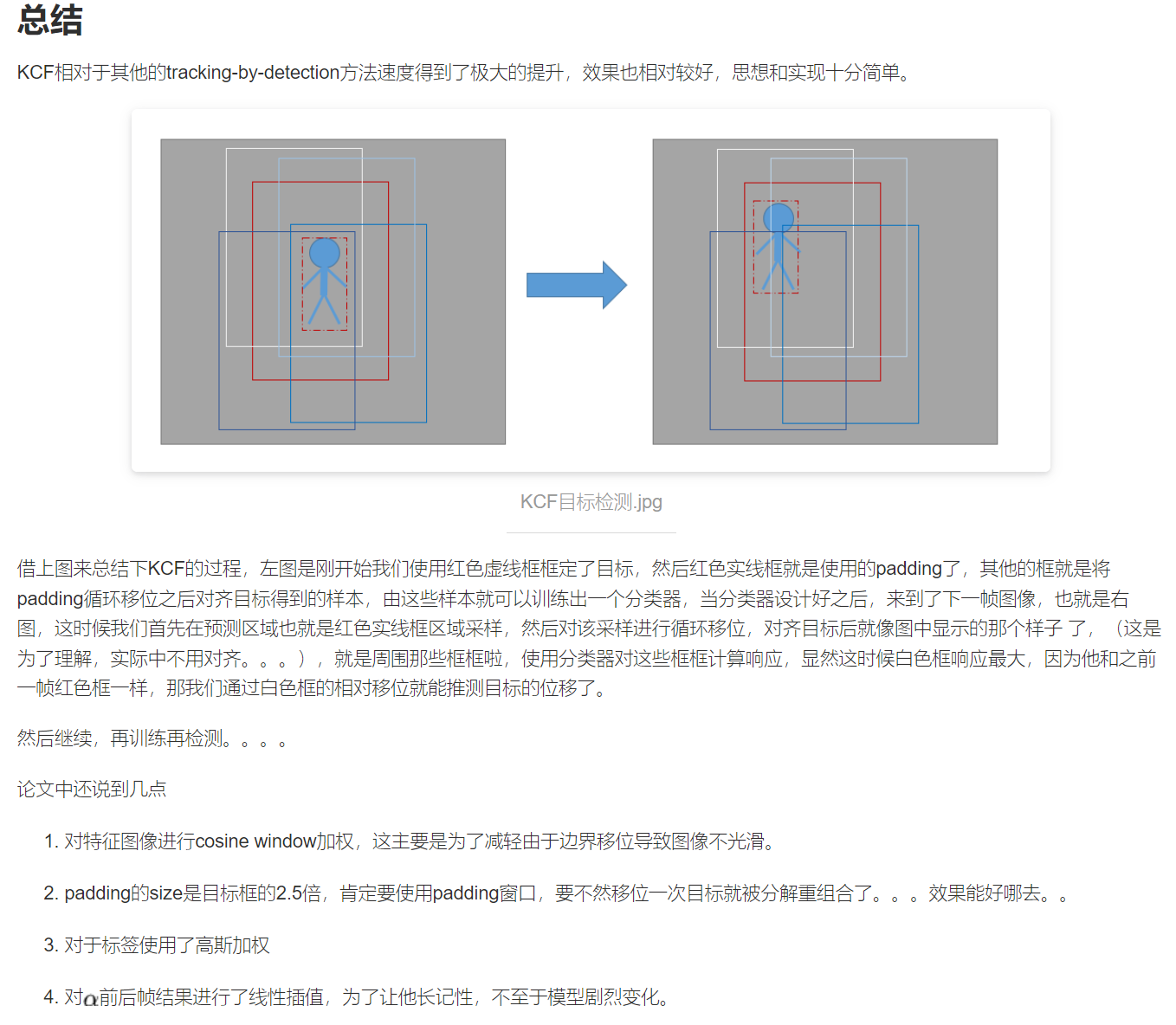
KCF
目录
- KCF
- 预备知识
- 1. 岭回归
- 2. 循环移位和循环矩阵
- 3. 傅里叶对角化
- 4. 方向梯度直方图(HOG)
- 正文
- 1. 线性回归
- 1.1. 岭回归
- 1.2. 基于循环矩阵获取正负样本
- 1.3. 基于傅里叶对角化的求解
- 2. 使用非线性回归对模型进行训练
- 2.1. 应用kernel-trick的非线性模型的求解结果
- 2.2. 快速核方法
- 2.3. 快速检测
- 3. 快速核相关
- 4. KCF算法流程
- 5. 总结
参考博文:
- 【KCF算法解析】High-Speed Tracking with Kernelized Correlation Filters笔记
- KCF论文理解与源码解析
- KCF算法公式推导
- KCF(High-Speed Tracking with Kernelized Correlation Filters)论文详解
- KCF目标跟踪方法分析与总结
预备知识
1. 岭回归
首先温习一下最小二乘法.
在矩阵形式下,最小二乘法的解
w
=
(
X
T
X
)
−
1
X
T
Y
w = (X^TX)^{-1}X^TY
w=(XTX)−1XTY,
X
X
X是一个
m
×
n
m×n
m×n的矩阵,其中每一行代表样本,列代表样本的某一个属性。为了求得
w
w
w,则必须要求矩阵
(
X
T
X
)
(X^TX)
(XTX)满秩(满秩是可逆的充要条件)。然而在解决现实问题时,当
X
X
X中的某些属性相关性较大时,
X
X
X不一定满秩(线性相关
⇔
\Leftrightarrow
⇔行列式为0
⇔
\Leftrightarrow
⇔矩阵不满秩)。除此之外,当
n
n
n的数量大于
m
m
m即样本矩阵的列数大于行数时,
X
X
X也不满秩,因为:

此时,由于
X
T
X
X^TX
XTX不满秩,则不可求其逆,因此无法算出最优解。那是否可以求一个近似最优解出来呢?
一个比较直观的想法是,在 X T X X^TX XTX中加上一个单位阵(即只有对角线有元素,其它处全为0的矩阵),该对角阵值的大小由一个参数 λ \lambda λ控制。
这样做的好处是,使得 X T X X^TX XTX变成满秩矩阵,这样是不是就可以求解了?而由于这个满秩矩阵是在原矩阵的基础上添加了扰动项(对角阵)得来的,所以最后求得的 w w w一般不是最优解,但是也是比较接近最优解了。(当最优解很难很难求解出时,可以较为简单地求出接近最优解的解一般是一种更好的选择)
最优解 w = ( X T X ) − 1 X T Y w = (X^TX)^{-1}X^TY w=(XTX)−1XTY,在加上由参数 λ \lambda λ控制的对角阵后,求得的次优解为 w = ( X T X + λ I n ) − 1 X T Y w = (X^TX+\lambda I_n)^{-1}X^TY w=(XTX+λIn)−1XTY ,其中:
-
I n I _n In是单位矩阵,对角线全是1,类似于“山岭”。
-
λ \lambda λ是岭系数,改变其数值可以改变单位矩阵对角线的值。
再反推目标函数,可以得到目标函数为:
arg min w ∣ ∣ X ⋅ w − Y ∣ ∣ 2 + λ ∣ ∣ w ∣ ∣ 2 \mathop{\arg\min}\limits_{w}||X \cdot w-Y||^2+\lambda||w||^2 wargmin∣∣X⋅w−Y∣∣2+λ∣∣w∣∣2
也就是说,岭回归其实就是在最小二乘法的基础上,加入了对 w w w的惩罚项,当 λ \lambda λ值越大时,惩罚强度就越大,生成的模型就越简单, ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2也被称为L2范数。从整体上来看,岭回归是对最小二乘回归的一种补充,其损失了无偏性,但是获得了较高计算精度和数值稳定性。
这篇岭回归详解 从零开始 从理论到实践讲得可以,还有这篇岭回归原理简单分析与理解。
2. 循环移位和循环矩阵
参考【KCF算法解析】High-Speed Tracking with Kernelized Correlation Filters笔记 理解即可,注意生成循环矩阵的过程用 X = C ( x ) X=C(x) X=C(x)表示,其中 x x x是原向量, X X X是生成的循环矩阵。
3. 傅里叶对角化
All circulant matrices are made diagonal by the Discrete Fourier Transform (DFT), regardless of the generating vector x.
任意循环矩阵可以被傅里叶变换矩阵对角化。
参照这篇博客循环矩阵傅里叶对角化理解即可,我也没太懂。
4. 方向梯度直方图(HOG)
图像特征:方向梯度直方图 HOG
正文
全文内容概览参考这篇目标跟踪算法——KCF入门详解即可。
公式推导参考这篇KCF算法公式推导即可。
1. 线性回归
1.1. 岭回归
KCF的基本模型是岭回归器。
线性分类器:
f
(
x
)
=
w
T
x
(1)
f(x)=w^Tx \tag 1
f(x)=wTx(1)
岭回归的目标函数:
arg
min
w
∣
∣
X
⋅
w
−
Y
∣
∣
2
+
λ
∣
∣
w
∣
∣
2
(2)
\mathop{\arg\min}\limits_{w}||X \cdot w-Y||^2+\lambda||w||^2 \tag 2
wargmin∣∣X⋅w−Y∣∣2+λ∣∣w∣∣2(2)
基于岭回归求得的闭式解(到底什么是“闭合解(Closed-form Solution)”):
w
=
(
X
T
X
+
λ
I
n
)
−
1
X
T
Y
(3)
w=(X^TX+\lambda I_n)^{-1}X^TY \tag 3
w=(XTX+λIn)−1XTY(3)
变换到复数域的闭式解:
w
=
(
X
H
X
+
λ
I
n
)
−
1
X
H
Y
(4)
w=(X^HX+\lambda I_n)^{-1}X^HY \tag 4
w=(XHX+λIn)−1XHY(4)
其中,
X
X
X表示样本矩阵,其中每一行代表每一个样本,每一列代表所有样本的某个特征值,
X
H
X^H
XH表示其复数的共轭转置。
1.2. 基于循环矩阵获取正负样本
假设感兴趣区域的图像patch由一个长度为 n n n的向量 x x x表示, x x x也被称作基样本。这个很好理解吧,目标跟踪一般是给定一组连续帧,以及需要跟踪的目标在起始帧的位置信息,然后在接下来的连续帧中执行跟踪。那么我们最开始能够获得的目标特征,就用 x x x表示。
之后,原文中的一句话提到:
Our goal is to train a classifier with both the base sample (a positive example) and several virtual samples obtained by translating it (which serve as negative examples).
即,**作者计划通过基样本来生成正负样本,然后送给分类器来训练,以获得区分目标区域和其它区域的能力。**这句话也很好理解吧,就是基于初始帧以及给定的目标信息,获得目标的特征,然后在此基础上生成正负样本,正样本代表需要跟踪的目标,负样本代表背景或者其它干扰信息。这是目标跟踪领域的一个常见思路,典型的如TLD、MOOSE都采用了这种方法。
如何基于基样本生成正负样本呢?这里得用前面提到的循环矩阵。
对于基样本 x x x,生成的循环矩阵 X = C ( x ) X=C(x) X=C(x),文中给了个示意图:
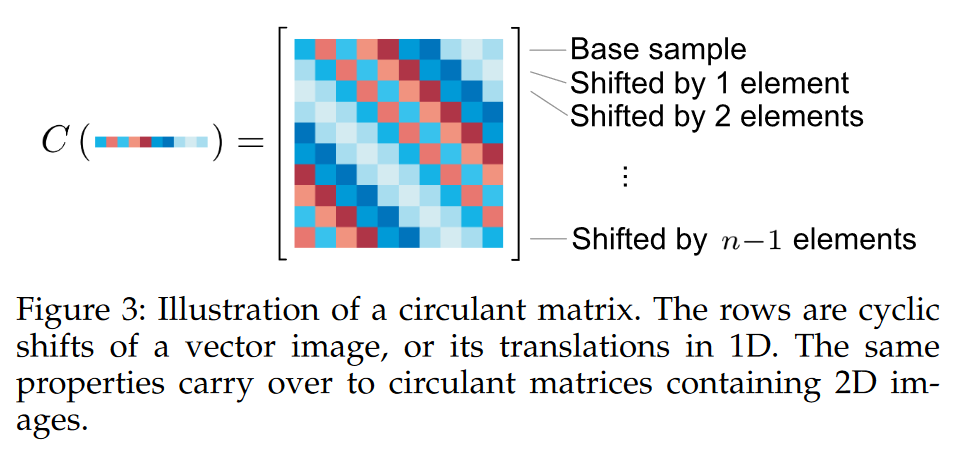
OK,此时,基于循环矩阵得到的正负样本,采用岭回归训练线性模型,得到在复数域下的解析解和前面的公式相同,但是公式中字母的意义不同:
w
=
(
X
H
X
+
λ
I
n
)
−
1
X
H
Y
(5)
w=(X^HX+\lambda I_n)^{-1}X^HY \tag 5
w=(XHX+λIn)−1XHY(5)
此时,
X
X
X表示由初始向量
x
x
x(基样本)生成的循环矩阵,
X
H
X^H
XH表示其复数的共轭转置,即
X
H
=
(
X
∗
)
T
X^H=(X^*)^T
XH=(X∗)T,
X
∗
X^*
X∗是
X
X
X的复数共轭形式。
1.3. 基于傅里叶对角化的求解
还记得前面提到的任意循环矩阵可以被傅里叶变换矩阵对角化吧,那么,用傅里叶对角化,我们就可以更快速地求解。
对于循环矩阵
X
X
X,其可以被傅里叶对角化:
X
=
C
(
x
)
=
F
d
i
a
g
(
x
^
)
F
H
(6)
X=C(x)=F \mathrm{diag}(\hat{x})F^H \tag 6
X=C(x)=Fdiag(x^)FH(6)
其中,
x
^
\hat{x}
x^是
x
x
x的离散傅里叶变换,即
x
^
=
F
(
x
⃗
)
\hat{x}=\mathcal{F}(\vec{x})
x^=F(x)。
F
F
F是离散傅里叶变换矩阵,是一个不依赖于
x
x
x的常数矩阵。注意,离散傅里叶变换矩阵是一个酉矩阵,即其满足
F
H
F
=
F
F
H
=
I
F^HF=FF^H=I
FHF=FFH=I。
之后,经过公式推导,参考KCF算法公式推导,可以得到线性模型参数
w
w
w的求解结果:
w
^
=
x
^
∗
⊙
y
^
x
^
∗
⊙
x
^
+
λ
(7)
\hat{w}=\frac{\hat{x}^*\odot \hat{y}}{\hat{x}^*\odot \hat{x}+\lambda} \tag 7
w^=x^∗⊙x^+λx^∗⊙y^(7)
注意,这里求出的
w
^
\hat{w}
w^是
w
w
w的傅里叶变换形式,使用逆向傅里叶变换即可以轻松地在空间域中恢复
w
w
w,这样我们就能在样本线性可分的前提下,基于训练样本,快速地求解出较优解
w
w
w(也就是能够快速地训练好分类模型)。
结果对比:
-
原闭式解 w = ( X H X + λ I n ) − 1 X H Y w=(X^HX+\lambda I_n)^{-1}X^HY w=(XHX+λIn)−1XHY的计算复杂度为 O ( n 3 ) O(n^3) O(n3)
-
简化后的解 w ^ = x ^ ∗ ⊙ y ^ x ^ ∗ ⊙ x ^ + λ \hat{w}=\frac{\hat{x}^*\odot \hat{y}}{\hat{x}^*\odot \hat{x}+\lambda} w^=x^∗⊙x^+λx^∗⊙y^的复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
所以,引入循环矩阵,不仅增强了样本,提高了准确率,而且简化了运算,提高了运行速度。
2. 使用非线性回归对模型进行训练
2.1. 应用kernel-trick的非线性模型的求解结果
上面只考虑了样本矩阵是线性可分的情况,而当数据在当前的特征空间中不能线性可分时,我们可以考虑把数据特征从当前特征空间映射到更高维的空间,从而使得在低维空间不可分的情况到高维空间之后就能变的线性可分了。核函数主要的目的就是把一个线性问题映射到一个非线性核空间,这样把在低维空间不可分的到核空间之后就能够可分了。
-
因此,需要找到一个非线性映射函数 φ ( x ) \varphi(x) φ(x),使得映射后的样本在高维空间中线性可分。那么在这个高维空间中,就可以**使用岭回归来寻找一个分类器 f ( x i ) = w T φ ( x i ) f(x_i)=w^T\varphi(x_i) f(xi)=wTφ(xi),**其中, φ ( x i ) \varphi(x_i) φ(xi)表示对样本 x i x_i xi通过非线性映射函数 φ \varphi φ变换到高维空间后的样本向量。
-
对于分类模型 f ( x i ) = w T φ ( x i ) f(x_i)=w^T\varphi(x_i) f(xi)=wTφ(xi), f ( x i ) f(x_i) f(xi)和 x i x_i xi都已知, φ ( ⋅ ) \varphi(\cdot) φ(⋅)取决于我们选取的映射函数,因此主要是想求得对 w w w的解,在使用Kernel-trick之后, w w w可以用训练样本的线性组合来表示:
w = ∑ i α i φ ( x i ) (8) w=\sum_i{\alpha_i \varphi(x_i)} \tag 8 w=i∑αiφ(xi)(8)
则最优化问题不再是求解 w w w,而是 α \alpha α。至于为什么可以将 w w w表示为样本的线性组合,可以参考这篇高维映射 与 核方法(Kernel Methods),里面有详细的解释,建议精读。 -
线性条件下的回归问题,经过非线性变换后,对于新样本 z z z的预测值为:
f ( z ) = w T z = ( ∑ i n α i φ ( x i ) ) T ⋅ φ ( z ) = ∑ i n α i φ ( x i ) T φ ( z ) = ∑ i n α i κ ( x i , z ) \begin{align*} f(z)&=w^Tz\\ &=(\sum_i^n{\alpha_i\varphi(x_i)})^T\cdot\varphi(z)\\ &=\sum_i^n{\alpha_i\varphi(x_i)}^T\varphi(z)\\ \tag9 &=\sum_i^n{\alpha_i\kappa(x_i,z)} \end{align*} f(z)=wTz=(i∑nαiφ(xi))T⋅φ(z)=i∑nαiφ(xi)Tφ(z)=i∑nαiκ(xi,z)(9)
其中, x i x_i xi代表训练分类器时的训练样本, z z z代表新出现的测试样本。即,预测其实是新样本与所有训练样本在高维空间中内积的加权平均。
对于
α
\alpha
α的求解,原文写得比较省略,原文中非线性情况下的最终求解结果(公式16)为
α
=
(
K
+
λ
I
)
−
1
y
(10)
\alpha=(K+\lambda I)^{-1}y \tag {10}
α=(K+λI)−1y(10)
注意,这里的优化目标不是用
w
w
w而是用字母
α
\alpha
α表示,
K
K
K代表核矩阵。
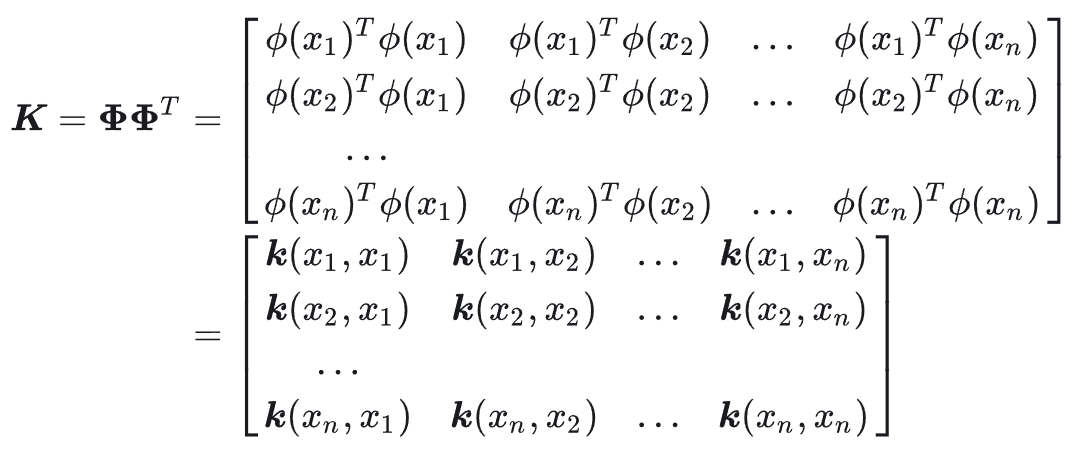
推导过程还是推荐仔细阅读这篇高维映射 与 核方法(Kernel Methods),阅读完之后也能了解什么是核技巧,以及为什么优化目标从线性可分情况下的 w w w换成了 α \alpha α。
2.2. 快速核方法
当采用基于Kernel trick的非线性模型训练时,最终求解目标 α = ( K + λ I ) − 1 y \alpha=(K+\lambda I)^{-1}y α=(K+λI)−1y包含了核矩阵 K K K。
而从核矩阵 K K K的公式中可以显而易见地发现,当数据样本量过大时,会导致核矩阵 K K K过大,从而使得计算的时间复杂度和空间复杂度都很高。
核方法并非没有缺点。原来的线性模型显然是一种参数化方法,好处是训练完成的模型只需要存储权重向量 。然而在使用了核方法以后,由于我们用训练集替换掉了权重项,因此相当于转化成了非参数化的方法,显然增加了需要存储的数据量,同时每一次做预测都需要用到全部训练数据集。
因此,本节中提到了一种快速的核回归方法。即怎么去计算核函数,怎么快速得到最优解。
原文的思路是:如果能证明核矩阵 K K K对于数据集来说是循环矩阵,就可以对其进行对角化,以加速求解过程。
通过施加一个条件来允许K循环。
定理一:给定循环矩阵 C ( x ) C(x) C(x),如果核函数 κ \kappa κ对于任何置换矩阵 M M M都满足 κ ( x , x ′ ) = κ ( M x , M x ′ ) \kappa(x,x')=\kappa(Mx,Mx') κ(x,x′)=κ(Mx,Mx′),则 C ( x ) C(x) C(x)在核函数 κ \kappa κ下对应的核矩阵 K K K是循环矩阵。
证明过程:假定有一个置换矩阵
P
P
P,如:
P
=
[
0
0
0
⋯
1
1
0
0
⋯
0
0
1
0
⋯
0
0
0
1
⋯
0
⋯
⋯
⋯
⋯
⋯
]
(11)
P=\begin{bmatrix} 0 & 0 & 0 & \cdots & 1\\ 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots\\ \end{bmatrix} \tag{11}
P=
0100⋯0010⋯0001⋯⋯⋯⋯⋯⋯1000⋯
(11)
即对于基样本
x
x
x,有:
x
1
=
P
0
x
=
x
=
[
x
1
,
x
2
,
⋯
,
x
n
]
T
x
2
=
P
1
x
=
[
x
n
,
x
1
,
⋯
,
x
n
−
1
]
T
⋯
x
n
=
P
n
−
1
x
=
[
x
2
,
x
3
,
⋯
,
x
1
]
T
(12)
x_1=P^0x=x=[x_1,x_2,\cdots,x_n]^T\\ x_2=P^1x=[x_n,x_1,\cdots,x_{n-1}]^T\\ \tag{12} \cdots \\ x_n=P^{n-1}x=[x_2,x_3,\cdots,x_1]^T
x1=P0x=x=[x1,x2,⋯,xn]Tx2=P1x=[xn,x1,⋯,xn−1]T⋯xn=Pn−1x=[x2,x3,⋯,x1]T(12)
则:
K
i
j
=
κ
(
x
i
,
x
j
)
=
κ
(
P
i
x
,
P
j
x
)
\begin{align*} K_{ij}&=\kappa(x_i, x_j) \\ \tag{13} &= \kappa(P^ix,P^jx)\\ \end{align*}
Kij=κ(xi,xj)=κ(Pix,Pjx)(13)
可以看到,从核矩阵
K
K
K的公式中,可以发现:
核矩阵中第 i i i行第 j j j列的值就是第 i i i和第 j j j个样本经过核函数之后得到的值再逐元素相乘计算出的内积。
而我们的样本矩阵是在基向量 x x x的基础上经过循环变换得到的循环矩阵,也就是说,这个式子,刚好满足我们之前的所有假设和前提。这里可能有点绕,得细细思考一会。
现在,由于定理中提到的是任意变换 M M M,那我们就假设 M M M这个置换矩阵为 P − i P^{-i} P−i。
由于
κ
(
x
,
x
′
)
=
κ
(
M
x
,
M
x
′
)
\kappa(x,x')=\kappa(Mx,Mx')
κ(x,x′)=κ(Mx,Mx′),所以有:
κ
(
M
x
i
,
M
x
j
)
=
κ
(
x
i
,
x
j
)
=
κ
(
P
−
i
P
i
x
,
P
−
i
P
j
x
)
=
κ
(
x
,
P
j
−
i
x
)
=
K
i
j
\begin{align*} \kappa(Mx_i, Mx_j)&=\kappa(x_i, x_j) \\ &= \kappa(P^{-i}P^ix,P^{-i}P^jx)\\ \tag{14} &= \kappa(x,P^{j-i}x)\\ &= K_{ij} \end{align*}
κ(Mxi,Mxj)=κ(xi,xj)=κ(P−iPix,P−iPjx)=κ(x,Pj−ix)=Kij(14)
由于
P
n
=
P
0
P^n=P^0
Pn=P0,也就是当
j
−
i
j-i
j−i的值每到
n
n
n时为一个循环,所以上式可以改写为
K
i
j
=
κ
(
x
,
P
(
j
−
i
)
m
o
d
n
x
)
K_{ij}=\kappa(x,P^{(j-i)mod\space n}x)
Kij=κ(x,P(j−i)mod nx),即:
K
=
[
κ
(
x
,
P
0
x
)
κ
(
x
,
P
1
x
)
⋯
κ
(
x
,
P
n
−
1
x
)
κ
(
x
,
P
1
x
)
κ
(
x
,
P
2
x
)
⋯
κ
(
x
,
P
0
x
)
⋮
⋮
⋱
⋮
κ
(
x
,
P
n
−
1
x
)
κ
(
x
,
P
0
x
)
⋯
κ
(
x
,
P
n
−
2
x
)
]
(15)
K=\begin{bmatrix} \kappa(x,P^{0}x) & \kappa(x,P^{1}x) & \cdots & \kappa(x,P^{n-1}x)\\ \kappa(x,P^{1}x) & \kappa(x,P^{2}x) & \cdots & \kappa(x,P^{0}x)\\ \vdots & \vdots & \ddots & \vdots \\ \tag{15} \kappa(x,P^{n-1}x) & \kappa(x,P^{0}x) & \cdots & \kappa(x,P^{n-2}x) \end{bmatrix}
K=
κ(x,P0x)κ(x,P1x)⋮κ(x,Pn−1x)κ(x,P1x)κ(x,P2x)⋮κ(x,P0x)⋯⋯⋱⋯κ(x,Pn−1x)κ(x,P0x)⋮κ(x,Pn−2x)
(15)
可以看到,此时核矩阵
K
K
K是一个循环矩阵。
原文中提到,下面的核函数都满足定理一:
- 径向基函数核,如:高斯核;
- 点积核,如:线性核、多项式核;
- 加权核,如:交集、 χ 2 \chi^2 χ2;
- 指数加权核
当 K K K为循环矩阵时,由前面关于循环矩阵的知识,可以得知核矩阵 K K K中的所有元素都是基于其第一行这个向量循环移位得到的。令 k x x k^{xx} kxx为核矩阵 K K K中的第一行向量,则 K = C ( k x x ) K=C(k^{xx}) K=C(kxx)。
原文中非线性情况下的最终求解结果(公式16)为
α
=
(
K
+
λ
I
)
−
1
y
(10)
\alpha=(K+\lambda I)^{-1}y \tag{10}
α=(K+λI)−1y(10)
由于
K
K
K为循环矩阵,则可以应用傅里叶对角化求解:
α
=
(
K
+
λ
I
)
−
1
y
=
(
C
(
k
x
x
)
+
λ
I
)
−
1
y
=
(
F
d
i
a
g
(
k
^
x
x
)
F
H
+
λ
I
)
−
1
y
=
(
F
d
i
a
g
(
k
^
x
x
+
λ
)
F
H
)
−
1
y
=
(
F
H
)
−
1
(
d
i
a
g
(
k
^
x
x
+
λ
)
−
1
)
F
−
1
y
=
F
d
i
a
g
(
k
^
x
x
+
λ
)
−
1
F
H
y
=
F
d
i
a
g
(
1
k
^
x
x
+
λ
)
F
H
y
\begin{align*} \alpha&=(K+\lambda I)^{-1}y\\ &=(C(k^{xx})+\lambda I)^{-1}y\\ &=(F\mathrm{diag}(\hat{k}^{xx})F^H+\lambda I)^{-1}y\\ &=(F\mathrm{diag}(\hat{k}^{xx}+\lambda)F^H)^{-1}y\\ &=(F^H)^{-1}(\mathrm{diag}(\hat{k}^{xx}+\lambda)^{-1})F^{-1}y\\ \tag{16} &=F\mathrm{diag}(\hat{k}^{xx}+\lambda)^{-1}F^Hy\\ &=F\mathrm{diag}(\frac{1}{\hat{k}^{xx}+\lambda})F^Hy \end{align*}
α=(K+λI)−1y=(C(kxx)+λI)−1y=(Fdiag(k^xx)FH+λI)−1y=(Fdiag(k^xx+λ)FH)−1y=(FH)−1(diag(k^xx+λ)−1)F−1y=Fdiag(k^xx+λ)−1FHy=Fdiag(k^xx+λ1)FHy(16)
这里用到了离散傅里叶变换矩阵是酉矩阵的性质,对公式两边进行离散傅里叶变换得到:
α
^
=
y
^
k
^
x
x
+
λ
(17)
\hat{\alpha}=\frac{\hat{y}}{\hat{k}^{xx}+\lambda} \tag{17}
α^=k^xx+λy^(17)
从上面这个公式,也就是原文中的公式(17)可以发现,当保证核矩阵
K
K
K为循环矩阵时,通过傅里叶对角化,可以使得对
α
\alpha
α的求解过程只需要涉及到核矩阵
K
K
K中的第一行向量
k
^
x
x
\hat{k}^{xx}
k^xx(
1
×
n
1\times n
1×n大小),而
k
^
x
x
\hat{k}^{xx}
k^xx是随着样本数量线性变化的。这意味着什么?传统的核方法需要计算一个
n
×
n
n\times n
n×n的核矩阵,与样本数量呈平方增长。
这意味着快速核方法大大节省了空间资源和时间资源。
2.3. 快速检测
在2.2节中,得到了系数 α \alpha α的简化求解形式(训练过程),而为了进一步提高算法的运行速度,文章对检测的过程也进行了简化加速。
首先由训练样本和其对应的标签训练检测器,其中训练集是由目标区域和由其移位得到的若干样本组成,对应的标签是根据距离越近正样本可能性越大的准则赋值的,然后可以得到 α \alpha α。
由式(9)可得,当对新样本
z
z
z(待检测的图像patch)进行检测时,有:
f
(
z
)
=
K
α
(18)
f(z)=K\alpha \tag{18}
f(z)=Kα(18)
注意,岭回归中包含的正则化只在训练时使用,对于预测,直接用求解好的
α
\alpha
α和核矩阵
K
K
K即可。
现在,用
K
z
K^z
Kz替换
K
K
K,考虑到实际情况,式(18)变为:
f
(
z
)
=
(
K
z
)
T
α
(19)
f(z)=(K^z)^T\alpha \tag{19}
f(z)=(Kz)Tα(19)
其中,
K
z
=
C
(
k
x
z
)
K^z=C(k^{xz})
Kz=C(kxz),表示训练样本和待检测样本之间的核矩阵,是一个非对称矩阵。
k
x
z
k^{xz}
kxz表示由基样本
x
x
x和基础待检测图像patch
z
z
z计算得到的核相关向量,
C
C
C仍代表循环位移操作。
由前面的内容易知, K z K^z Kz中的元素可以被表示为 κ ( P i − 1 z , P j − 1 x ) \kappa(P^{i-1}z,P^{j-1}x) κ(Pi−1z,Pj−1x), P P P的定义如式(11)所示。
基于定理一,同样可以证明训练样本和检测样本之间的核矩阵
K
z
K^z
Kz为循环矩阵,因此可以对其进行傅里叶对角化,有:
f
(
z
)
=
(
K
z
)
T
α
=
(
C
(
k
x
z
)
)
T
α
=
(
F
d
i
a
g
(
k
^
x
z
)
F
H
)
T
α
=
F
H
d
i
a
g
(
k
^
x
z
)
F
α
\begin{align*} f(z)&=(K^z)^T\alpha \\ &=(C(k^{xz}))^T\alpha\\ &=(F\mathrm{diag}(\hat{k}^{xz})F^H)^T\alpha \\ \tag{20} &=F^H\mathrm{diag}(\hat{k}^{xz})F\alpha \end{align*}
f(z)=(Kz)Tα=(C(kxz))Tα=(Fdiag(k^xz)FH)Tα=FHdiag(k^xz)Fα(20)
考虑到离散傅里叶变换矩阵
F
F
F的性质,则有:
F
f
(
z
)
=
d
i
a
g
(
k
^
x
z
)
F
α
(21)
Ff(z)=\mathrm{diag}(\hat{k}^{xz})F\alpha \tag{21}
Ff(z)=diag(k^xz)Fα(21)
舍掉
F
F
F,再进行傅里叶变换,则可以得到最终的快速检测公式:
f
^
(
z
)
=
k
^
x
z
⊙
α
^
(22)
\hat{f}(z)=\hat{k}^{xz}\odot\hat{\alpha} \tag{22}
f^(z)=k^xz⊙α^(22)
该公式可以理解为用
α
\alpha
α对核矩阵
K
z
K^z
Kz进行空间滤波操作(或者是线性加权),生成的
f
(
z
)
f(z)
f(z)是一个向量,代表所有可能位置的置信度值,最大的置信度值对应的patch即作为检测的输出。
3. 快速核相关
尽管前面已经提出了快速训练和快速检测的方法,但它们仍依赖于计算两个图像块的核相关性这一过程(如 k x x k^{xx} kxx和 k x z k^{xz} kxz),根据前面的内容,核相关操作包含了计算两个输入(及所有相对位移)的高维特征点乘值,这是最后一个需要解决的计算瓶颈。因此本节对核相关过程进行了加速。
这一节主要就是介绍几种常见的核函数的形式,以及每种核函数所对应的快速计算方式。
-
点积核:
k x x ′ = g ( F − 1 ( x ^ ∗ ⊙ x ^ ′ ) ) (23) k^{xx'}=g(\mathcal{F}^{-1}(\hat{x}^*\odot\hat{x}')) \tag{23} kxx′=g(F−1(x^∗⊙x^′))(23) -
多项式核:
k x x ′ = ( F − 1 ( x ^ ∗ ⊙ x ^ ′ ) + a ) b (24) k^{xx'}=(\mathcal{F}^{-1}(\hat{x}^*\odot\hat{x}')+a)^b \tag{24} kxx′=(F−1(x^∗⊙x^′)+a)b(24) -
对于某种径向基函数 h h h,其核函数可表示为:
k x x ′ = h ( ∣ ∣ x ′ ∣ ∣ 2 + ∣ ∣ x ∣ ∣ 2 − 2 F − 1 ( x ^ ∗ ⊙ x ^ ′ ) ) (25) k^{xx'}=h(||x'||^2+||x||^2-2\mathcal{F}^{-1}(\hat{x}^*\odot\hat{x}')) \tag{25} kxx′=h(∣∣x′∣∣2+∣∣x∣∣2−2F−1(x^∗⊙x^′))(25) -
高斯核:
k x x ′ = e x p ( − 1 σ 2 ( ∣ ∣ x ′ ∣ ∣ 2 + ∣ ∣ x ∣ ∣ 2 − 2 F − 1 ( x ^ ∗ ⊙ x ^ ′ ) ) ) (26) k^{xx'}=exp(-\frac{1}{\sigma^2}(||x'||^2+||x||^2-2\mathcal{F}^{-1}(\hat{x}^*\odot\hat{x}'))) \tag{26} kxx′=exp(−σ21(∣∣x′∣∣2+∣∣x∣∣2−2F−1(x^∗⊙x^′)))(26)
4. KCF算法流程