一、Objects元素的隐藏与显示
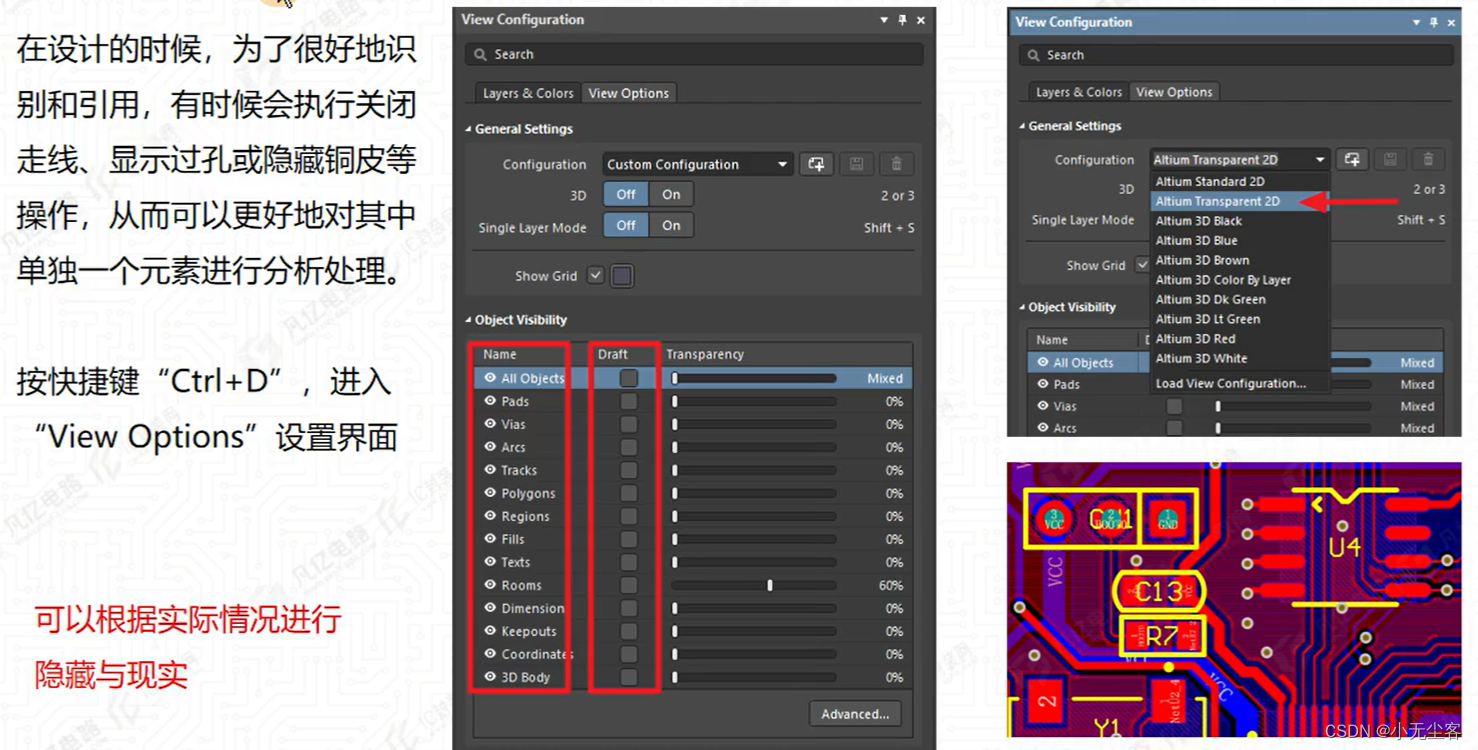
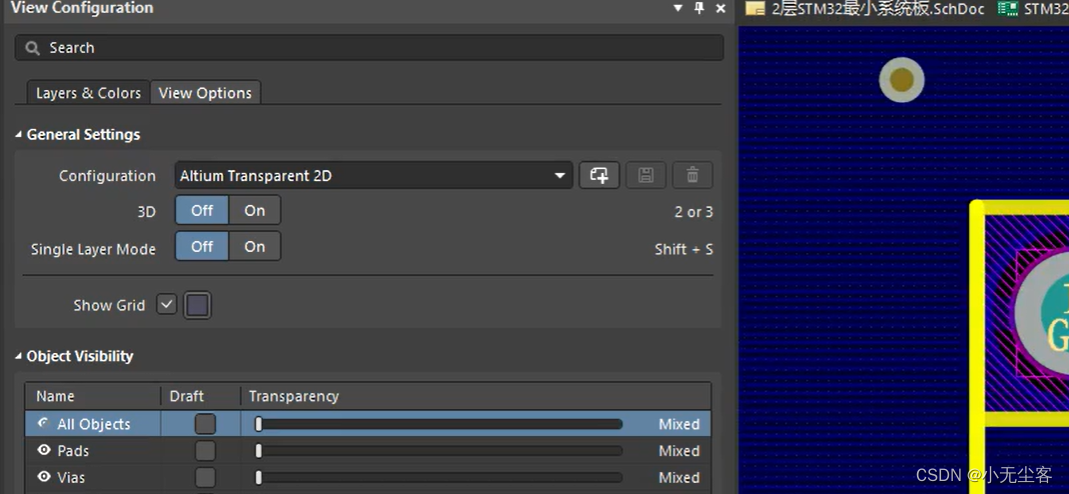
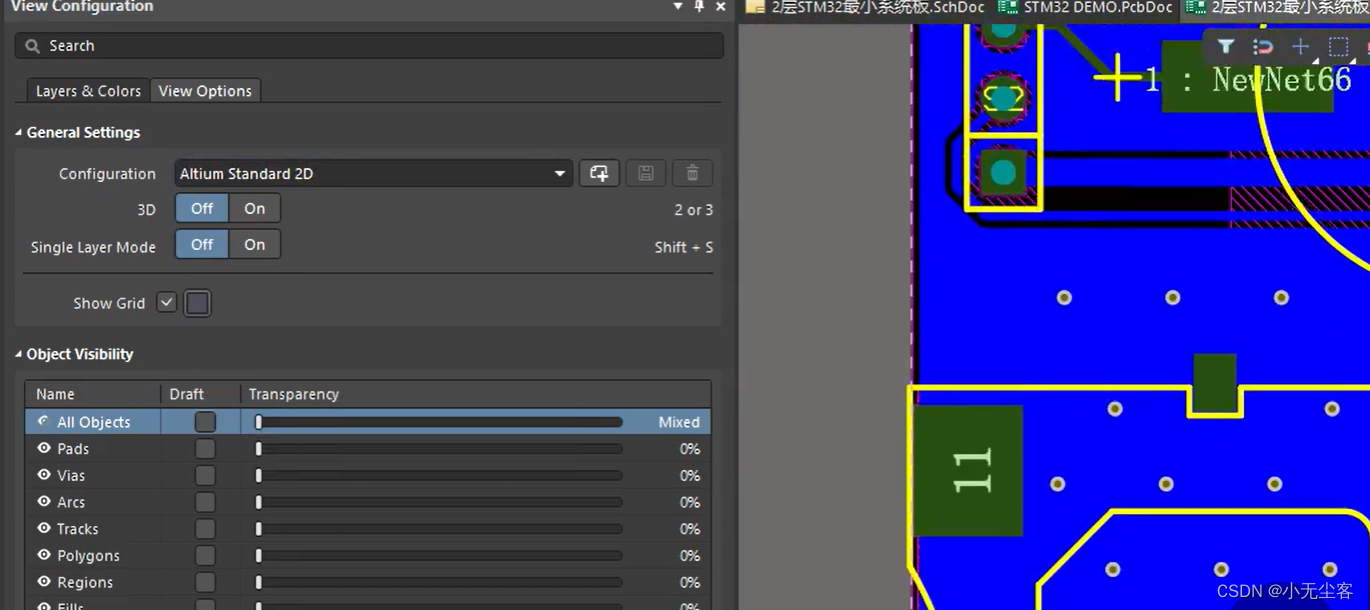
1、Altium Transparent 2D与Altium Standard 2D的区别
1) Altium Transparent 2D
2) Altium Standard 2D
二、特殊复制粘贴
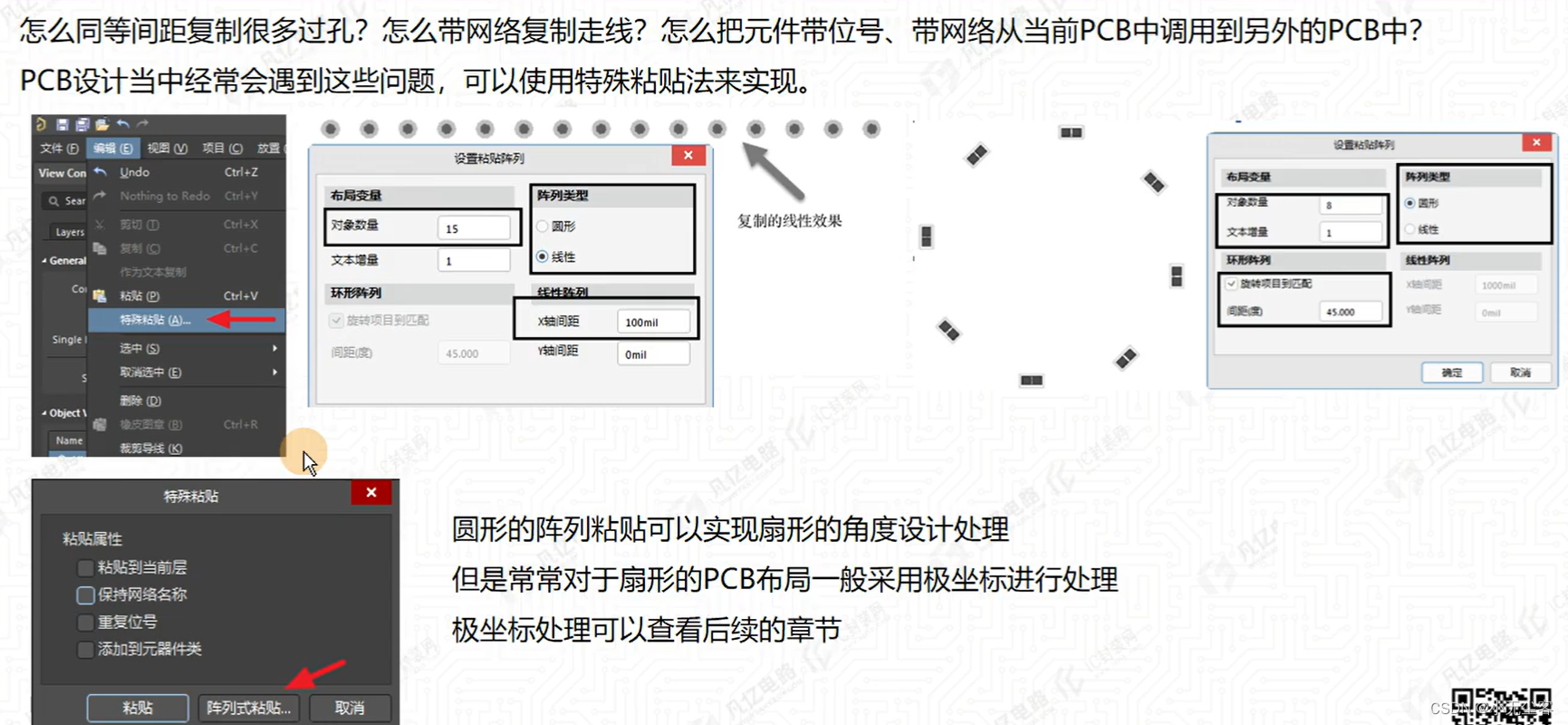
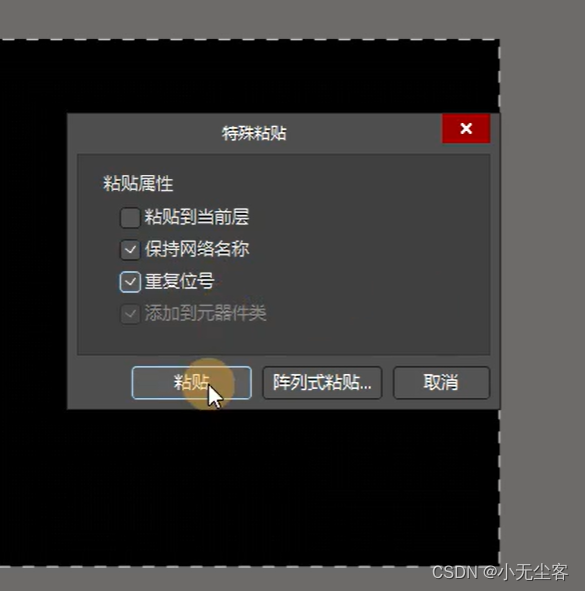
1、如何把元件带位号、带网络从当前PCB调用到另外的PCB中
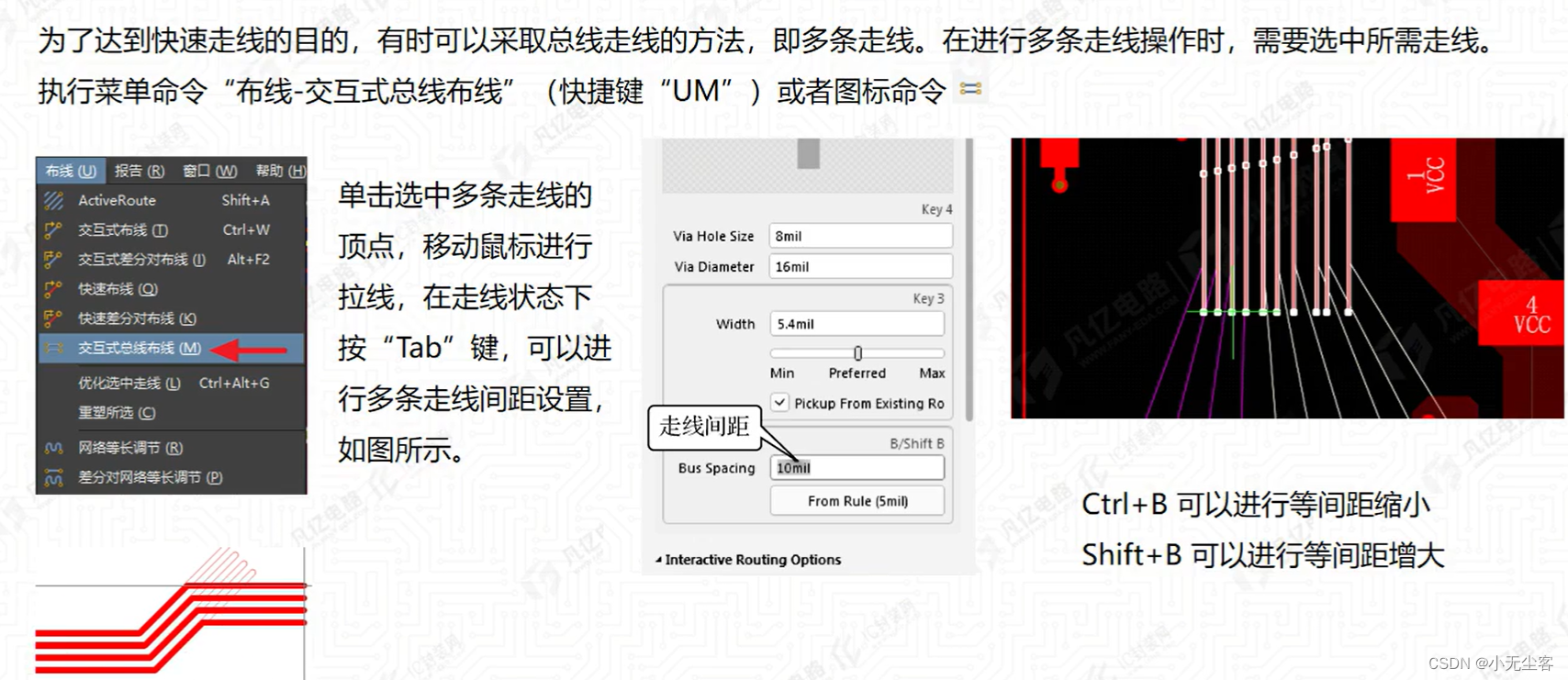
三、多根走线与多根走线设置
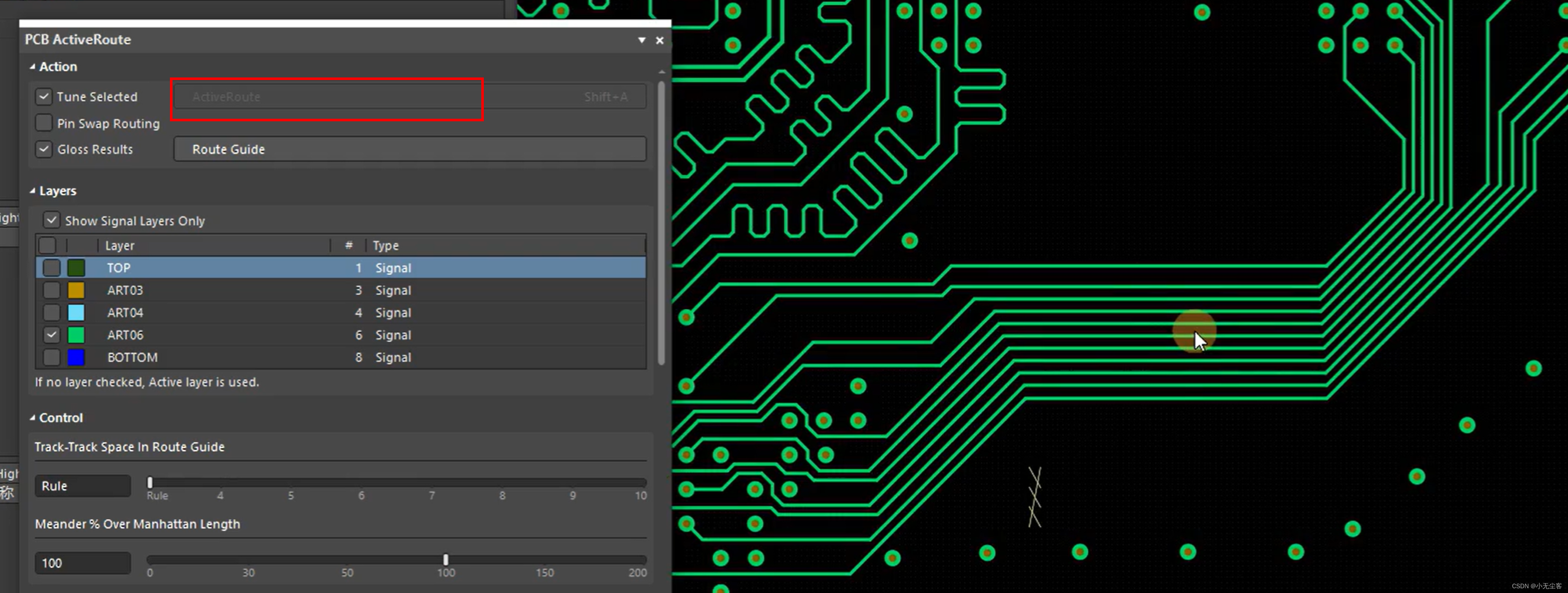
四、Active Route 的自动布线辅助
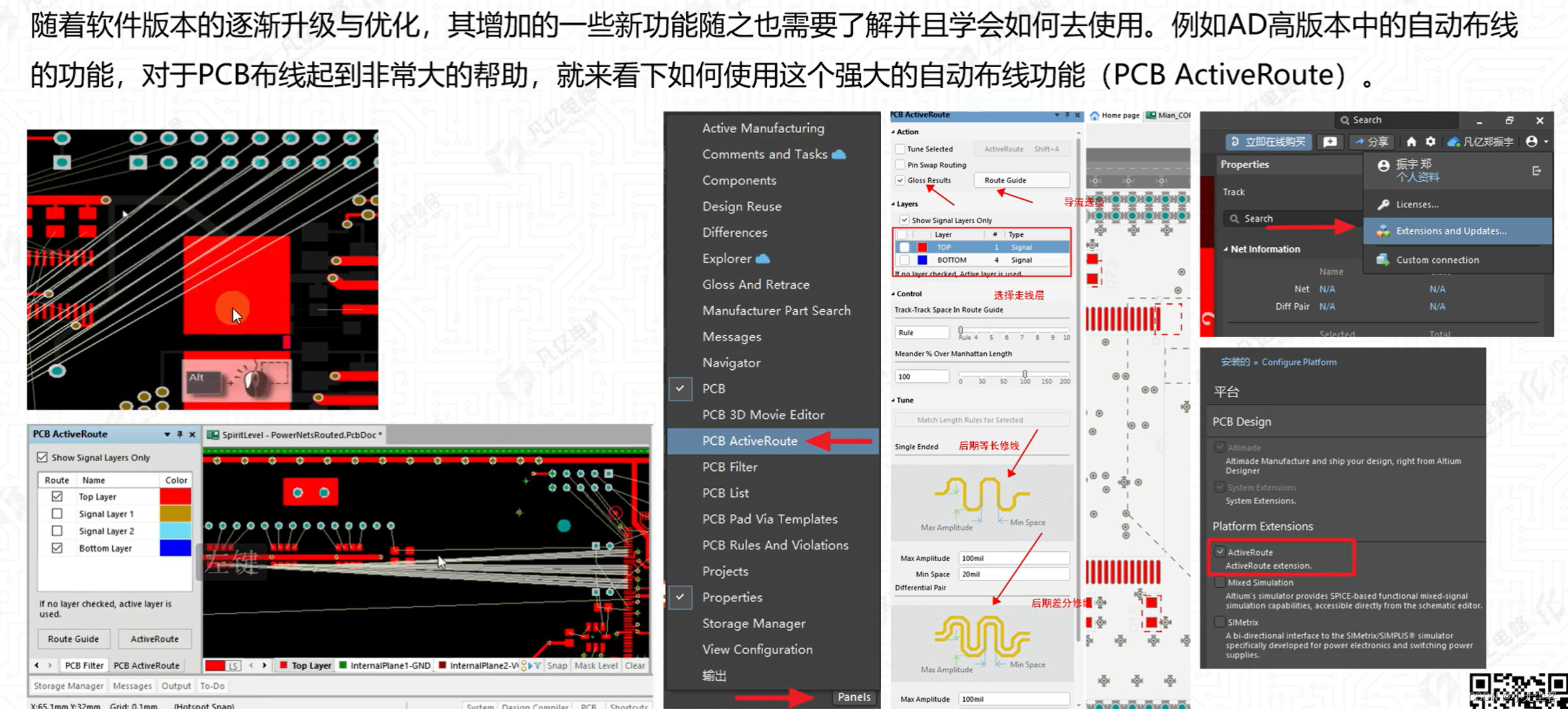
1、点击Panels-PCB Active Route
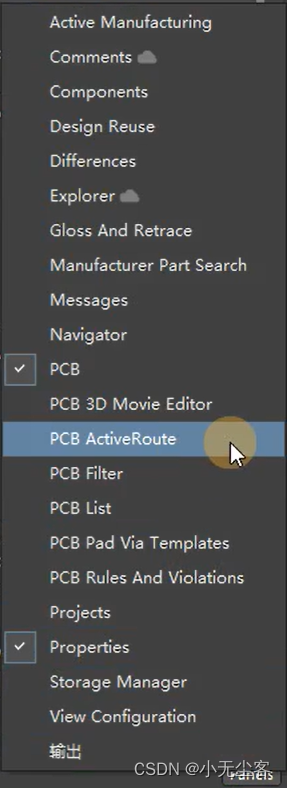
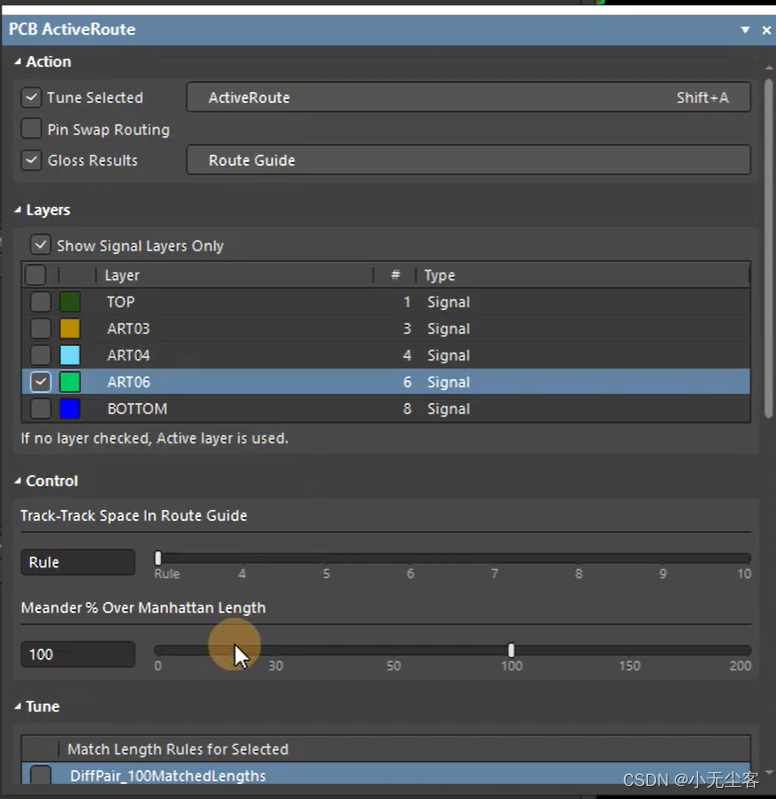
选择所在层
2、点击红色框,进行大体路径描绘
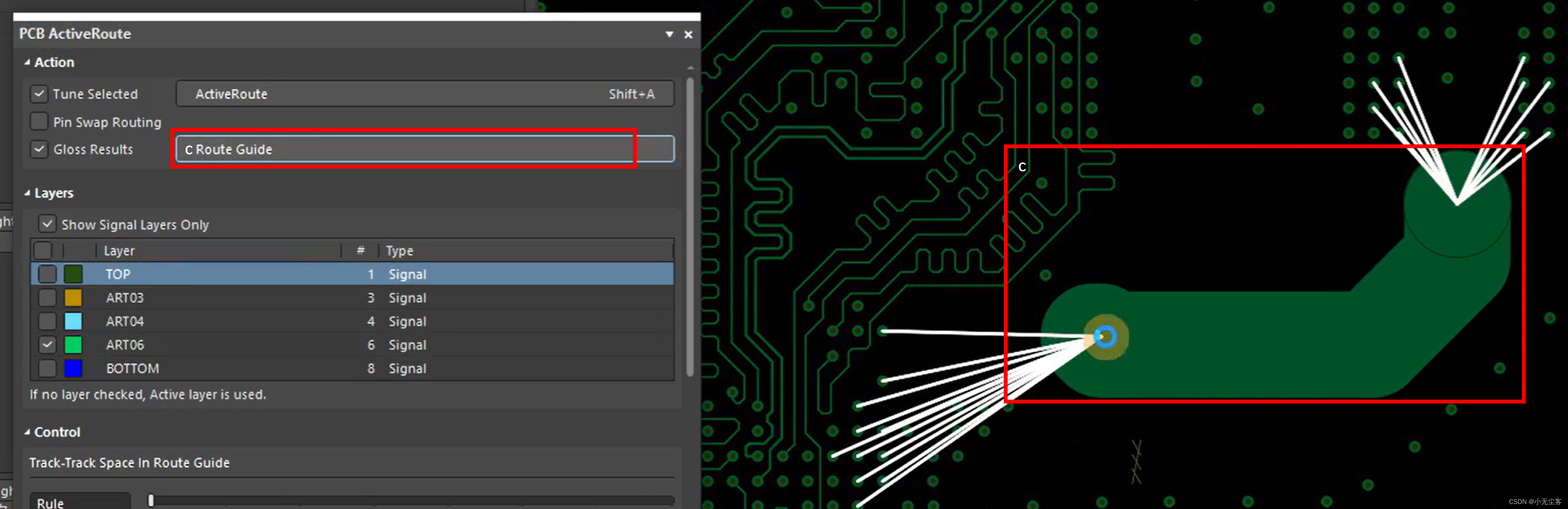
3、点击红色框,即可完成自动布线
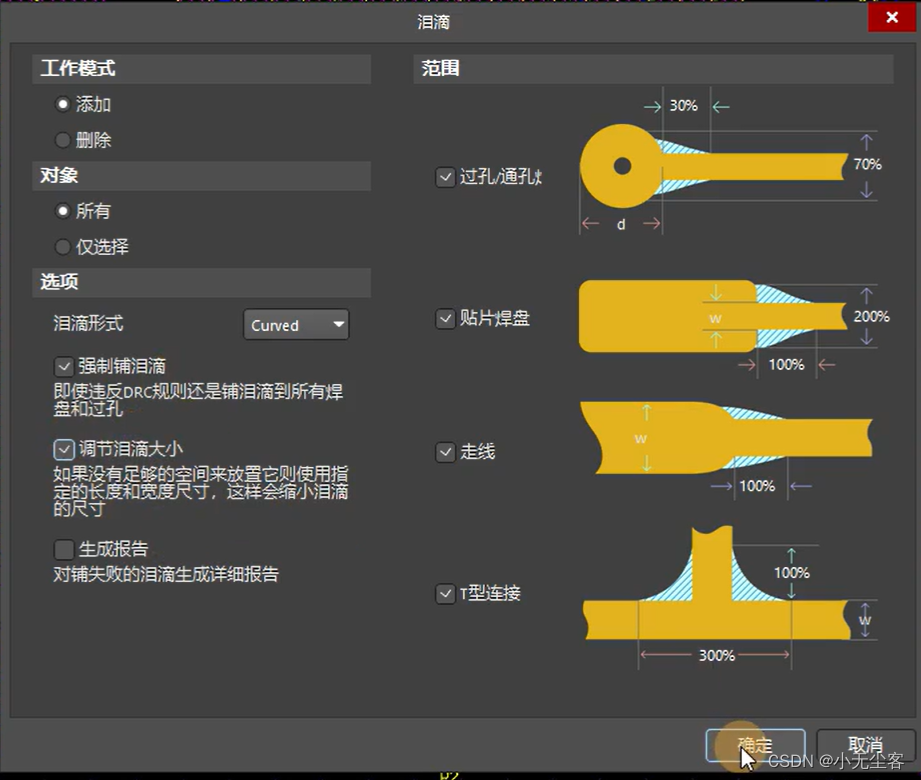
五、泪滴
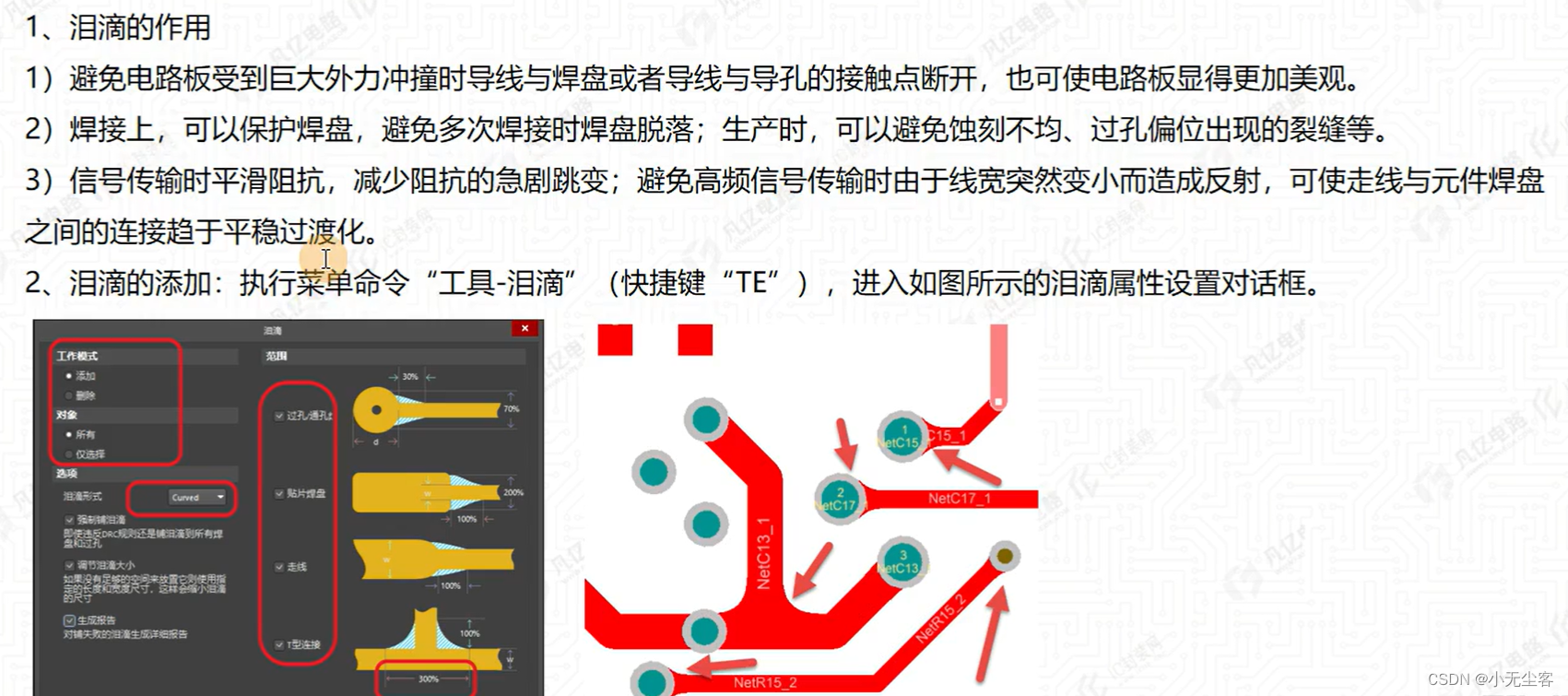
1、先将铜皮移开,在进行泪滴添加;最后再恢复

2、参数设置