信号系统之窗口正弦滤波器

1 Windowed-Sinc 的策略

图 16-1 说明了 windowed-sinc 滤波器背后的思想。在**(a)**中，显示了理想低通滤波器的频率响应。所有低于截止频率 $f_c$ 的频率都以单位振幅通过，而所有较高的频率都被阻挡。通带是完全平坦的，阻带中的衰减是无限的，两者之间的过渡是无限小的。

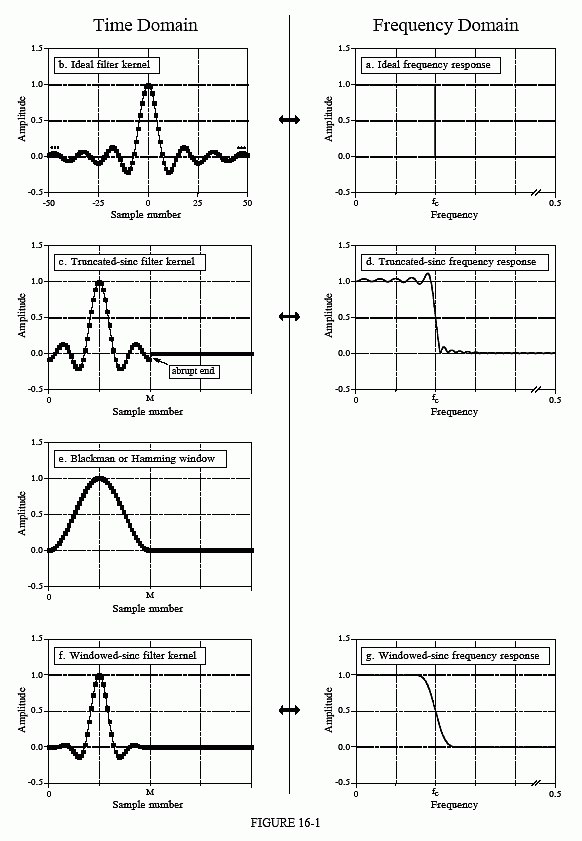
采用该理想频率响应的逆傅里叶变换产生理想滤波器核(脉冲响应)，如 (b) 所示。该曲线的一般形式称为 sinc 函数，由下式给出：

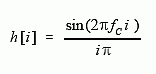
使用该滤波器内核对输入信号进行卷积可提供完美的低通滤波器。问题是，sinc 函数继续到负无穷大和正无穷大，而不会下降到零振幅。虽然这种无限长度对数学来说不是问题，但它对计算机来说是一个障碍。

为了解决这个问题，将对(b)中的 sinc 函数进行两次修改，得到©中所示的波形：

首先，它被截断为 M+1 点，在主瓣周围对称选择，其中 M 是偶数。这些 M+1 点之外的所有样本都设置为零，或者干脆忽略。
其次，整个序列向右移动，使其从 0 到 M。这允许仅使用正索引来表示筛选器内核。虽然许多编程语言允许负索引，但它们使用起来很麻烦。滤波器内核中这种 M/2 位移的唯一效果是将输出信号偏移相同的量。

由于修改后的滤波器内核只是理想滤波器内核的近似值，因此它不会具有理想的频率响应。为了找到获得的频率响应，可以对©中的信号进行傅里叶变换，从而得到(d)中的曲线。通带中存在过大的纹波和阻带中的衰减不良。这些问题是由于截断的 sinc 函数末端的突然不连续性造成的。增加过滤器内核的长度并不能减少这些问题；无论 M 产生多长时间，不连续性都是显着的。

幸运的是，有一种简单的方法可以改善这种情况。图(e)显示了一条平滑的锥形曲线，称为Blackman window。将截断的 sinc©乘以 Blackman 窗口(e)，得到(f)中所示的** windowed-sinc 滤波器内核**。这个想法是减少截断末端的突兀性，从而改善频率响应。图(g)显示了这种改进。通带现在是平坦的，阻带衰减非常好，在这张图中看不到。

有几种不同的窗口可用，其中大多数以 1950 年代的原始开发人员命名。只有两个值得使用，Hamming window 和 Blackman window，这些是由以下方式给出的：

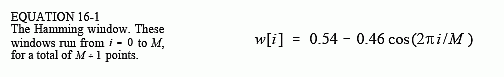
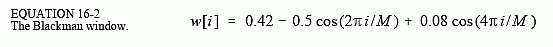
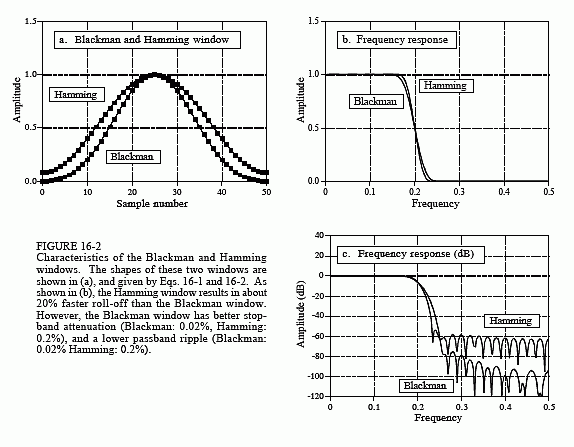
图 16-2a 显示了这两个窗口的形状(即曲线中总共 51 个点)。应该使用这两个窗口中的哪一个？ 这是 参数之间的权衡。如图 16-2b 所示，汉明窗的滚降速度比布莱克曼快约 20%。然而（c）表明Blackman具有更好的阻带衰减。Blackman 的阻带衰减为 -74dB(∼0.02%)，而汉明的阻带衰减仅为 -53dB(∼0.2%)。虽然在这些图中看不到，但布莱克曼的通带纹波仅为0.02%左右，而汉明纹波通常为0.2%。一般来说，布莱克曼应该是第一选择；缓慢的滚降比不良的阻带衰减更容易处理。

2 设计过滤器

要设计窗口正弦，必须选择两个参数：截止频率 $f_c$ 和滤波器核的长度 M。截止频率为表示为采样率的分数，因此必须介于 0 和 0.5 之间。M 的值根据近似值设置滚降：

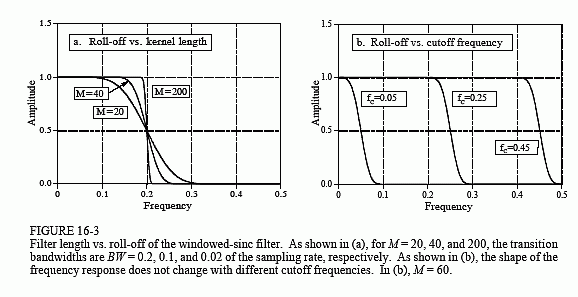
其中 BW 是过渡带的宽度，从曲线几乎不离开 1 的地方到几乎达到零的地方（例如，曲线的 99% 到 1%）测量。转换带宽也表示为采样频率的分数，并且必须在 0 和 0.5 之间。图 16-3a 显示了如何使用此近似值的示例。所示的三条曲线是从具有以下条件的过滤器内核生成的：M=20、40和200。从方程 16-3 可以看出，转换带宽分别为：BW=0.2、0.1和0.02。图(b)显示，频率响应的形状不取决于所选的截止频率。

由于卷积所需的时间与信号的长度成正比，方程 16-3 表示计算时间（M 的值）和滤波器锐度（BW 的值）之间的权衡。例如，Blackman 窗口的滚降速度慢了 20%（与汉明相比），可以通过使用长 20% 的滤波器内核来补偿。换句话说，可以说布莱克曼窗口的执行速度比等效的滚降汉明窗口慢 20%。这很重要，因为 windowed-sinc 过滤器的执行速度已经非常慢了。

如图16-3b所示，windowed-sinc滤波器的截止频率是在半振幅点处测量的。为什么使用 0.5 而不是模拟电子和其他数字滤波器中使用的标准0.707(-3dB)？这是因为窗口正弦波的频率响应在通带和阻带之间是对称的。例如，汉明窗口产生的通带纹波为 0.2%，阻带衰减（即阻带中的纹波）为 0.2%。其他滤波器不显示这种对称性，因此在使用一半振幅点来标记截止频率时没有优势。这种对称性使窗口正弦成为光谱反演的理想选择。

选择 $f_c$ 和 M 后，根据以下关系计算过滤器内核：

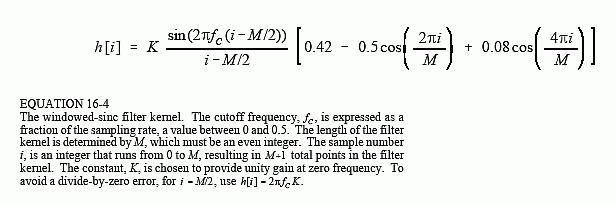
根据前面的讨论，应该能够识别三个组成：sinc 函数、M/2 移位和 Blackman 窗口。为了使滤波器在直流时具有单位增益，必须选择常数 K，使所有样本的总和等于1。在实践中，在计算滤波器核时忽略 K，然后根据需要对所有样本进行归一化。表 16-1 中列出的程序显示了如何完成此操作。还要注意计算是如何在 sinc 的中心 = M/2 处处理的，这涉及除以零。

具体说明方程 16-4 描述的过滤器内核在计算机阵列中的位置。例如，M 将被选为 100。M 必须是偶数。筛选器内核中的第一个点位于数组位置 0，而最后一个点位于数组位置 100。整个信号的长度为 101 个点。对称中心位于点 50，即 M/2。点 50 左边的 50 个点与右边的 50 个点是对称的。点 0 与点 100 的值相同，点 49 与点 51 相同。如果滤波器内核中必须有特定数量的样本，例如要使用 FFT，只需在一端或另一端添加零即可。例如，当 M = 100 时，可以使样本 101 到 127 等于零，从而产生一个 128 点长的滤波器核。

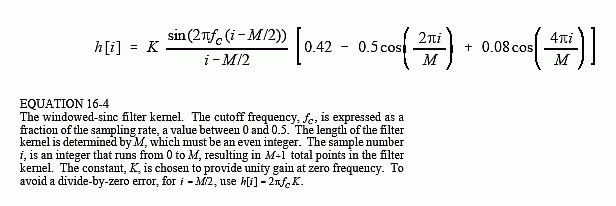
图 16-4 显示了 windowed-sinc 滤波器内核的示例及其相应的阶跃响应。过滤器内核开头和结尾的样本非常小，甚至在图形中都看不到它们。不要错误地认为它们不重要！这些样本的价值可能很小；但是，它们共同对滤波器的性能有很大影响。这也是为什么浮点表示通常用于实现窗口化 sinc 滤波器的原因。整数通常没有足够的动态范围来捕获筛选器内核中包含的值的大量变化。windowed-sinc滤波器在时域中的表现如何？阶跃响应有过冲和振铃；这不是对时域中编码信息的信号的过滤器。

3 Windowed-Sinc滤波器示例

脑电图（EEG）是大脑电活动的测量值。它可以被检测为出现在连接到头部表面的电极上的毫伏级信号。大脑中的每个神经细胞都会产生小的电脉冲。脑电图是以（希望）协调的方式产生大量这些电脉冲的综合结果。尽管对思维和这种电协调之间的关系知之甚少，但脑电图中的不同频率可以通过特定的心理状态来识别。如果您闭上眼睛放松，主要的脑电图模式将在大约 7 到 12 赫兹之间缓慢振荡。这种波形称为alpha rhythm，与满足感和注意力水平下降有关。睁开眼睛环顾四周，脑电图会变为β节律，频率在17到20赫兹之间。其他频率和波形见于儿童、不同深度的睡眠以及各种脑部疾病，如癫痫。

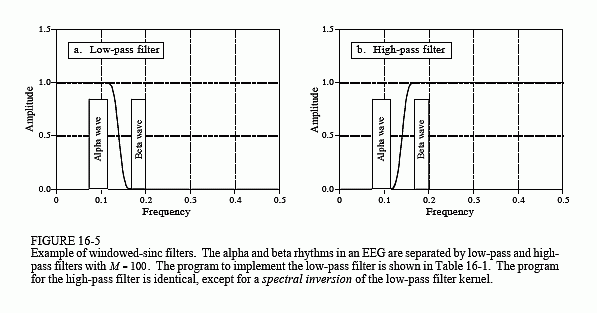
在这个例子中，将假设脑电信号已被模拟电子设备放大，然后以每秒 100 个样本的采样率进行数字化。采集数据 50 秒会产生 5,000 个点的信号。目标是将 alpha 节律与 beta 节律分开。为此，将设计一个截止频率为 14 赫兹或 0.14 的数字低通滤波器的采样率。转换带宽将设置为 4 赫兹，即采样率的 0.04。从方程 16-3 开始，滤波器内核需要大约 101 个点长，将任意选择使用汉明窗口。表 16-1 中的程序显示了如何执行过滤器。滤波器的频率响应由滤波器核的傅里叶变换得到，如图16-5所示。

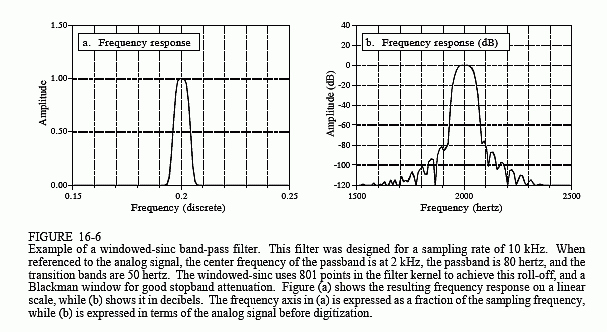
在第二个示例中，将设计一个带通滤波器来隔离音频信号中的信号音，例如当按下电话上的按钮时。假设信号已在 10 kHz 下数字化，目标是隔离以 2 kHz 为中心的 80 赫兹频段。在采样率方面，希望阻断所有低于 0.196 和高于 0.204 的频率（分别对应于 1960 赫兹和 2040 赫兹）。为了实现 50 赫兹（采样率的 0.005）的转换带宽，将滤波器内核设置为 801 个点长，并使用布莱克曼窗口。表 16-2 包含用于计算滤波器内核的程序，而图 16-6 显示了频率响应。设计涉及几个步骤。首先，设计了两个低通滤波器，一个截止值为0.196，另一个截止值为0.204。然后，第二个滤光片在光谱上反转，使其成为高通滤波器。接下来，添加两个滤波器核，产生带阻滤波器。最后，另一个光谱反转使其成为所需的带通滤波器。

4 将其推向极限

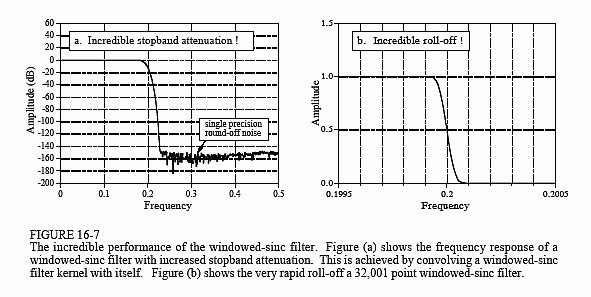
windowed-sinc滤波器可以被推到令人难以置信的性能水平，而不会出现令人讨厌的意外。例如，假设需要隔离 120 伏电源线上的 1 毫伏信号。低通滤波器将需要阻带衰减至少为 -120dB。如前所述，Blackman 窗口仅提供 -74dB（五千分之一）。幸运的是，更容易获得更大的阻带衰减。输入信号可以使用传统的windowed-sinc滤波器内核进行滤波，从而提供中间信号。然后，中间信号可以第二次通过滤波器，进一步将阻带衰减提高到-148dB（3000万分之），也可以将两个阶段组合成一个过滤器。组合滤波器的核等于两级滤波器核的卷积。这也意味着，将任何滤波器内核与自身卷积会产生一个具有显着改善阻带衰减的滤波器内核。付出的代价是更长的滤波器内核和更慢的滚降。图 16-7a 显示了 201 点低通滤波器的频率响应，该滤波器是通过将 101 点布莱克曼窗口正弦与自身卷积而形成的（如果确实需要超过-100dB的阻带衰减，则应使用双精度。单精度通带内信号的舍入噪声可能不规则地出现在阻带中，幅度在-100dB至-120dB范围内）。

图 16-7b 显示了窗口化 sinc 令人难以置信的性能的另一个示例：内核中具有 32,001 个点的低通滤波器。频率响应符合预期，采样率为0.000125。这个过滤器有多好？尝试构建一个模拟电子滤波器，以小于 0.02% 的变化将信号从 DC 传递到 1000 赫兹，并以小于 0.02% 的残余阻断阻断 1001 赫兹以上的所有频率。现在这是一个过滤器！请记住图 16-7 中的两个过滤器都使用单精度。使用双精度可以使这些性能级别扩展一百万倍。