GWO（灰狼优化器）是一种群体智能优化算法，它模拟了灰狼的社会结构和狩猎行为。GWO算法通过模拟灰狼的等级制度、狩猎策略和搜索机制来寻找问题的最优解。而K-means是一种经典的聚类算法，用于将数据点划分为K个簇。将GWO优化算法应用于K-means聚类中，主要是为了解决K-means算法对初始簇中心敏感和容易陷入局部最优解的问题。

以下是GWO优化K-means的原理和过程的详细介绍：

1. GWO算法原理

GWO算法模拟了灰狼的等级制度、狩猎策略和搜索机制。在灰狼群体中，存在三种角色：α狼（领导者）、β狼（次领导者）和δ狼（底层成员）。GWO算法通过模拟这三种角色的行为来更新搜索代理（即候选解）的位置。

搜索机制：

• 追踪：灰狼会追踪、包围并逼近猎物。在算法中，这表现为搜索代理向当前最优解（α狼）靠近。
• 骚扰：灰狼会骚扰猎物，使其向群体中心移动。在算法中，这表现为搜索代理向群体中心移动。
• 攻击：当灰狼足够接近猎物时，它们会发动攻击。在算法中，这表现为搜索代理根据α狼、β狼和δ狼的位置来更新自己的位置。

2. GWO优化K-means的过程

将GWO算法应用于K-means聚类的主要目的是优化初始簇中心的选择，以避免陷入局部最优解。

步骤1：初始化

• 选择要聚类的数据集和簇的数量K。
• 使用GWO算法初始化搜索代理（即候选簇中心）的位置。

步骤2：计算适应度函数

• 对于每个搜索代理（簇中心组合），使用K-means算法将数据点分配到最近的簇中心。
• 计算每个簇内数据点的平均距离（或其他合适的距离度量）作为适应度函数值。这个值反映了聚类效果的好坏。

步骤3：更新搜索代理位置

• 根据GWO算法的搜索机制（追踪、骚扰、攻击）更新搜索代理的位置。
• 新的位置代表新的簇中心组合。

步骤4：重复优化过程

• 重复步骤2和3，直到达到预定的迭代次数或适应度函数值不再显著改进。
• 在每次迭代中，记录当前最优的簇中心组合和对应的适应度函数值。

步骤5：输出最终聚类结果

• 使用最终的最优簇中心组合，使用K-means算法将数据点分配到最近的簇中心，得到最终的聚类结果。

通过将GWO算法与K-means聚类相结合，可以更有效地选择初始簇中心，并提高聚类效果。同时，GWO算法的全局搜索能力也有助于避免K-means算法陷入局部最优解的问题。

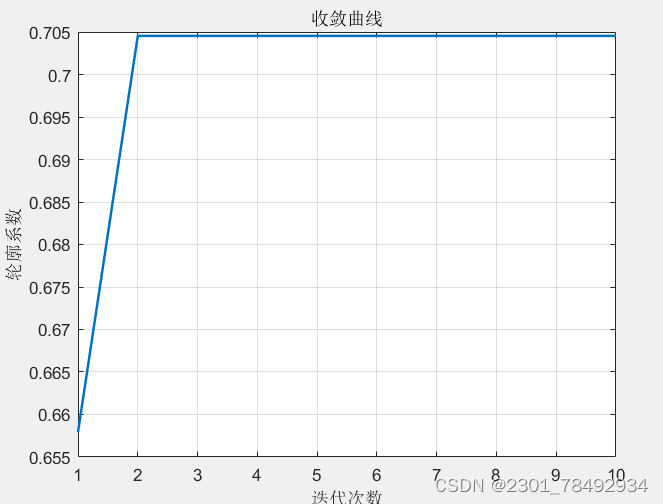
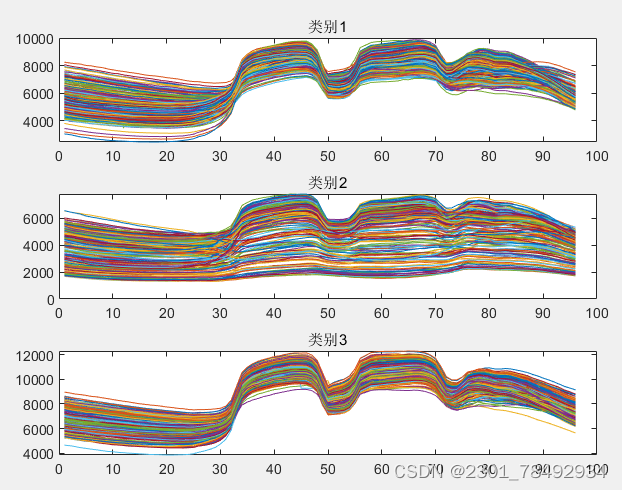
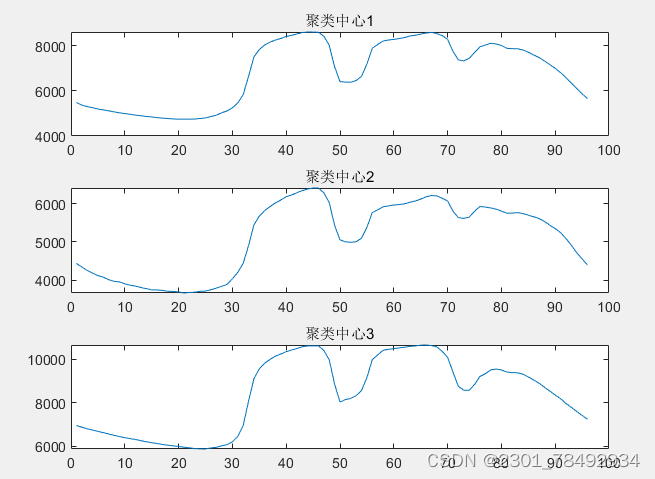
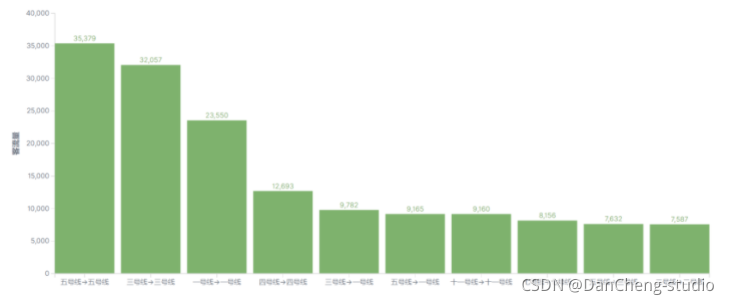
算法效果如下: