目录
选择排序
SelectSort直接选择排序
整体思路
图解分析
代码实现
时间复杂度
选择排序
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
- 直接选择排序是暴力选数值。
- 堆排序是在堆的结构上选数值。
SelectSort直接选择排序
- 在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素。
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换。
- 在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素。
- 优化:遍历一遍同时选取最小的和最大的值同时放在第一位和最后一位(存在一个坑)
直接选择排序的特性总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
整体思路
- 在元素集合array[i]--array[n-1]中选择关键码最大(小)的数据元素。
- 若它不是这组元素中的最后一个(第一个)元素,则将它与这组元素中的最后一个(第一个)元素交换。
- 在剩余的array[i]--array[n-2](array[i+1]--array[n-1])集合中,重复上述步骤,直到集合剩余1个元素。
- 优化:遍历一遍同时选取最小的和最大的值同时放在第一位和最后一位(存在一个坑)
- 优化:本来是一次选出最小的,优化之后一次选出最小的和最大的。
- 在a[0]~a[n-1]遍历中选出最大的数和最小的数的下标
- 最大的数的下标:maxi 最小的数的下标:mini
- 最大的数的位置的下标:begin = 0
- 最小的数的位置的下标:end = n-1
- 选出元素下标和对应位置的下标,的元素交换,不是覆盖❗
- 重复上诉过程,然后begin-- / end++ 直到它们相遇(begin < end )
- 注意❗最大值元素的下标maxi可能与最小值的元素的位置begin下标重叠,导致交换完最小值a[begin]和a[mini]交换之后的那个位置的元素不是最大值maxi而是最小值mini。
- ❗注意这里交换的是数值,下标没有交换🆗也就是说交换完之后maxi&mini任然指向原来的位置
图解分析 
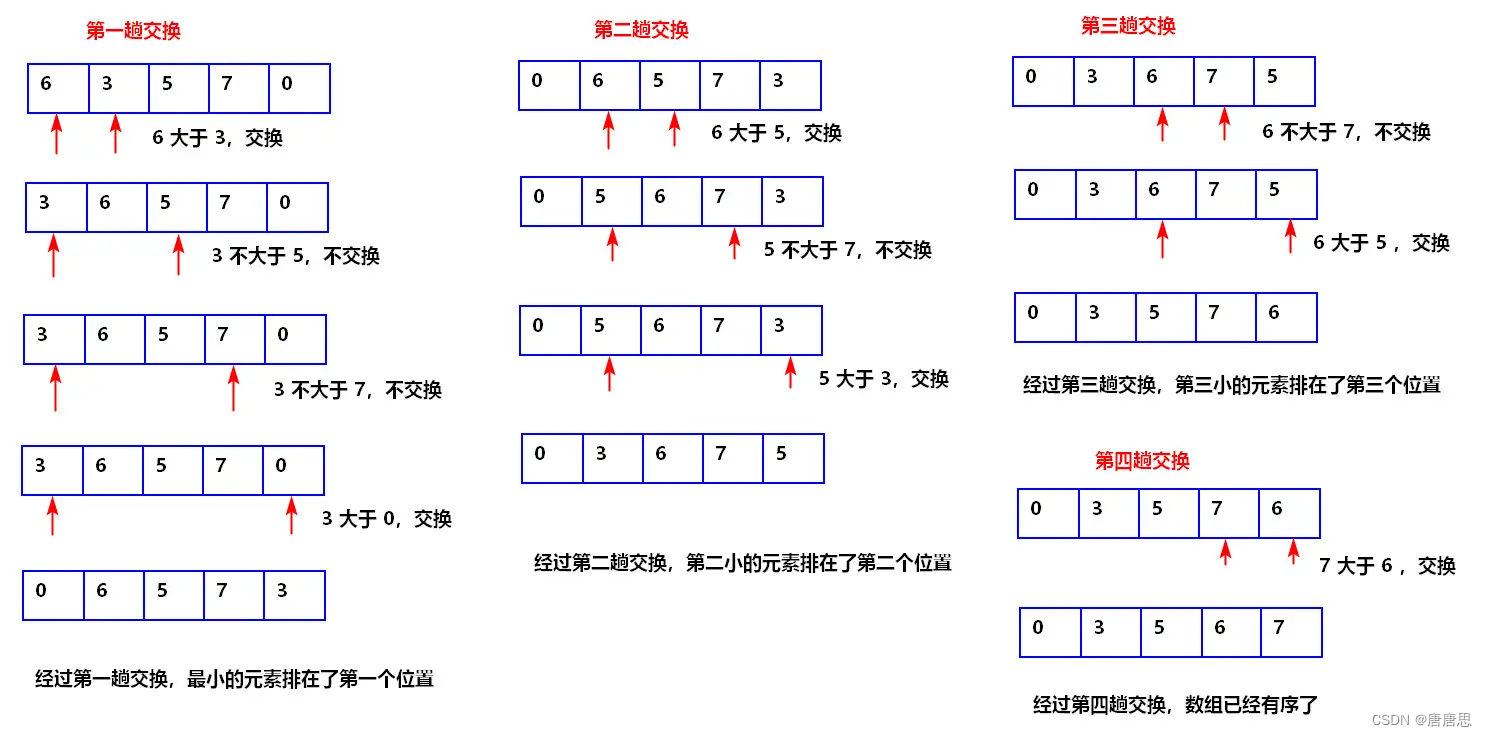 大家可以自己尝试画优化版的选择排序🆗
大家可以自己尝试画优化版的选择排序🆗
2,4,3,2,6,5,1,8,9,10,0
- 每次遍历的i的范围[begin,end](begin和end是变化的)
- 最大值元素的下标maxi可能与最小值的元素的位置begin下标重叠
- ❗注意这里交换的是数值,下标没有交换🆗也就是说交换完之后maxi&mini任然指向原来的位置


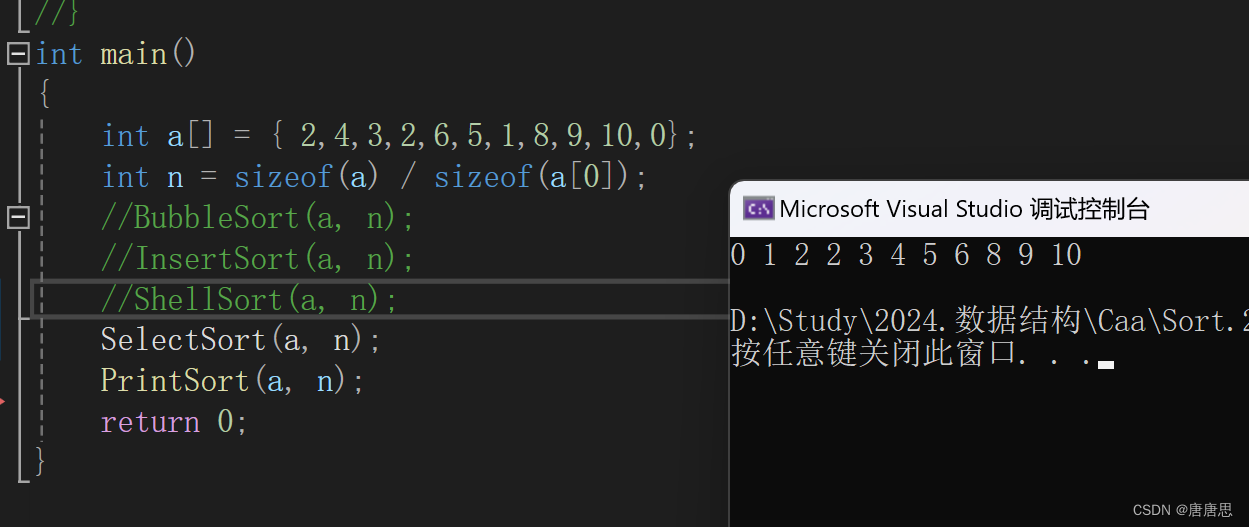
代码实现
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
int maxi = begin;
int mini = begin;
while (begin < end)
{
//遍历区间在[begin,end]
for (int i = begin; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = i;
}
if (a[i] > a[maxi])
{
maxi = i;
}
//>=/<=不换
}
Swap(&a[mini], &a[begin]);
if (a[maxi] == a[begin])
{
maxi = mini;
}
Swap(&a[maxi], &a[end]);
begin++;
end--;
}
}
时间复杂度
时间复杂度:O(N^2)
等差数列

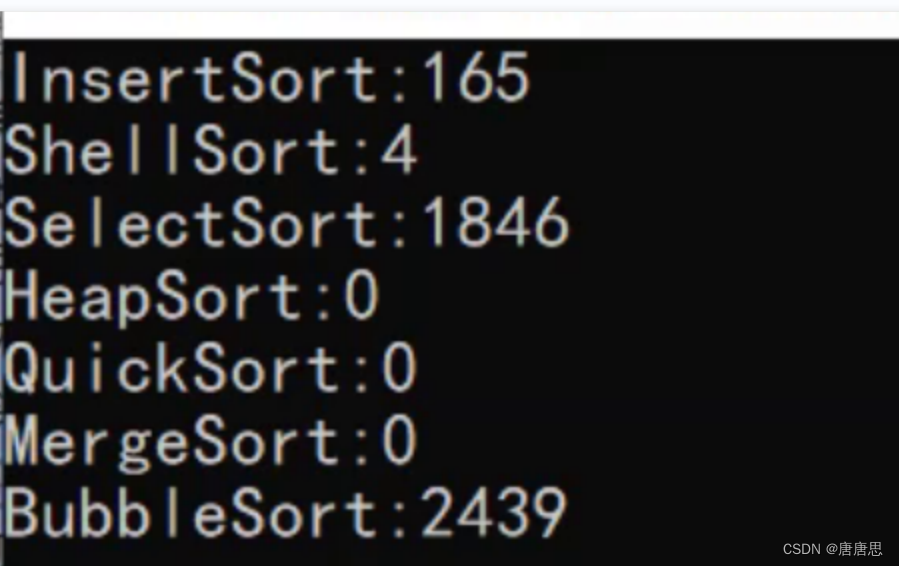
- 最后会总结稳定性和各个排序效率比较
- 数据量不同,各个排序相对效率就是不同,不能确定
🙂感谢大家的阅读,若有错误和不足,欢迎指正。下篇堆排序回顾。