在上一章，我们了解了扩散模型的基本原理，但它离实现Stable Diffusion的文生图或图生图功能显然还有一段距离，那就是如何将文字或图片信息融入到生成图片的过程中，比如，像下图这样？

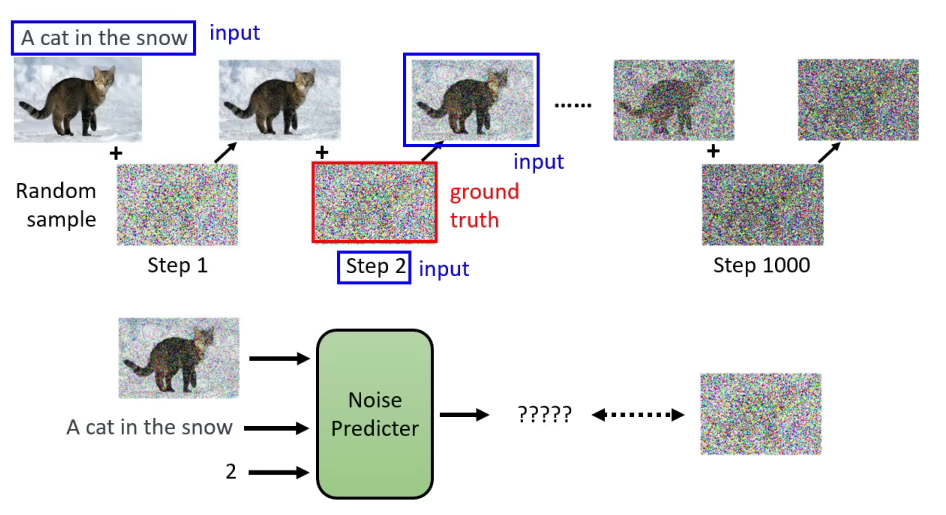
除此之外，扩散模型的一个重要特点就是维度的不变性，这就限制了生成图片大小的上限，原始论文中最大的图片生成大小也就是256×256，这意味着所有的中间表示也是这个尺度，如果再大一点，显卡和耐心可能就不够用了。

LDM

为了解决上述两个难题，我们需要在隐空间中重新审视扩散过程，并基于此重新设计生成模型，这也是Stable Diffusion的直接原理。这里我们要读一篇发表于CVPR2022的论文：《High-Resolution Image Synthesis with Latent Diffusion Models》

概述

论文提出了一个名为Latent Diffusion Models (LDM)的新模型，旨在减少直接在像素空间中训练扩散模型所带来的计算复杂度。论文的主要内容和贡献如下：

• 提出了两阶段训练方法：首先训练一个自动编码器，学习一个低维的潜在空间表示，然后在自动编码器的潜在空间中训练扩散模型。这显著降低了训练和推理的计算复杂度。
• 引入交叉注意力机制：通过将交叉注意力层添加到UNet中，LDM可以处理各种条件输入，如文本或语义布局，并实现高质量的图像生成。
• 在多个任务上取得了最先进或竞争性的性能，包括无条件图像生成、文本到图像生成、语义合成、超分辨率和图像修复等。相比像素级扩散模型，LDM的训练和推理成本大大降低。

原理

作者认为任何生成性学习方法都有两个主要阶段：感知压缩和语义压缩。

感知压缩指的是在训练过程中，自动编码器通过学习去除图像中不太重要的细节信息，保留基本的结构和语义信息。在这个过程中，图像的高频细节信息被过滤掉，留下低频语义信息。这种压缩方式对减少计算复杂度和模型参数是有帮助的。

语义压缩则是指生成模型学习语义和概念层面的信息，通过生成过程来弥补感知压缩过程中丢失的细节。这种压缩方式能够有效提升模型的生成能力，同时减少对不重要的细节的建模。

两种压缩相结合，也就是自编码器和扩散过程相结合，也就有了LDM模型。

模型架构

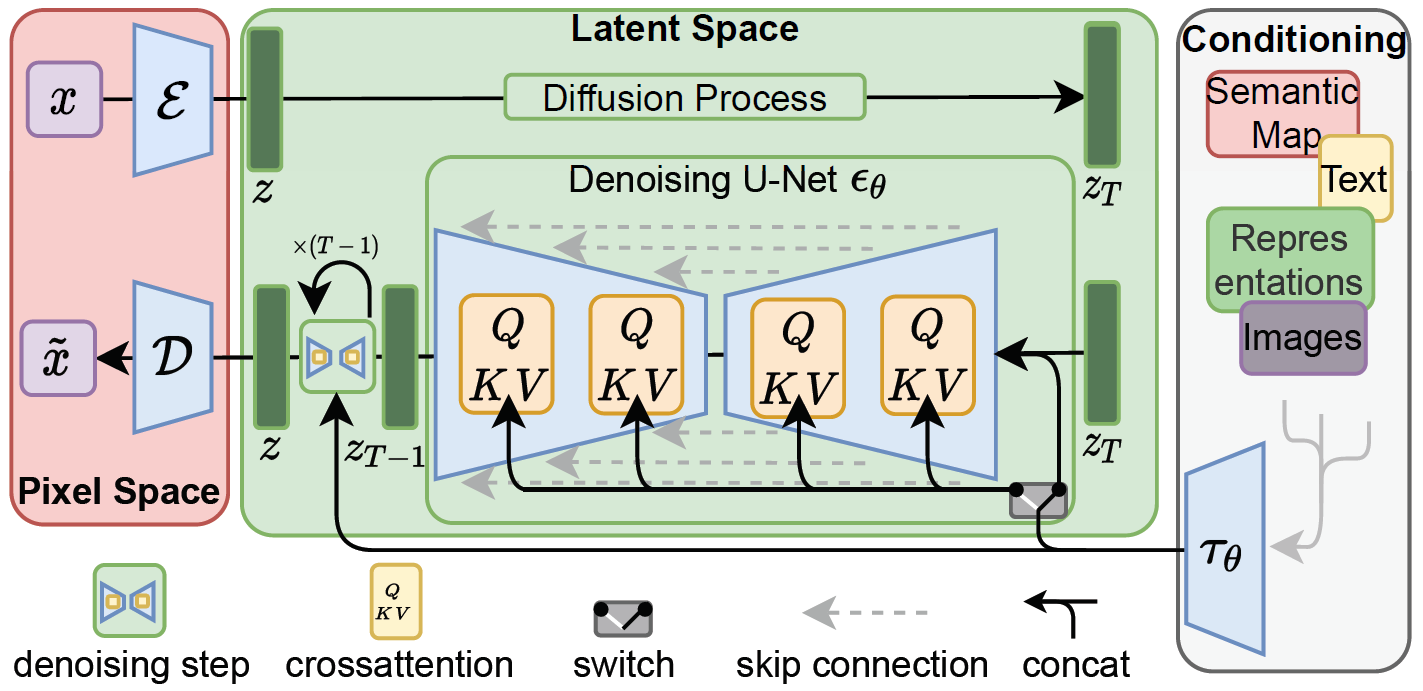
模型的总体架构如下图所示，包括了左侧用来实现感知压缩的变分自编码器模型（VAE）、中间在潜空间完成扩散过程的Unet模型，以及右侧的条件引导模型。

自编码器模型

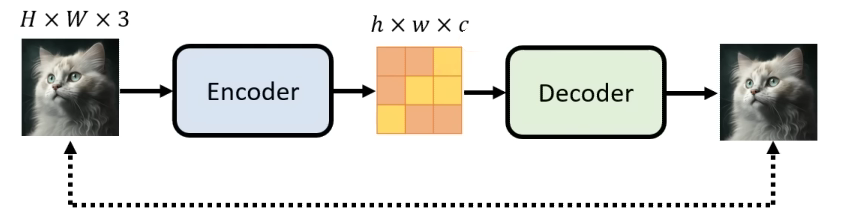
给定原始图像$x\in R^{H\times W\times 3}$，编码器$\mathcal{E}$将其编码为隐空间中的表示，即$z=\mathcal{E}(x)$，其中$z\in R^{h\times w\times c}$。这里我们定义降采样率$f=H/h=W/w$。

解码器$\mathcal{D}$用来实现从隐空间到像素空间的转换，即$\tilde{x}=\mathcal{D}(z)=\mathcal{D}(\mathcal{E}(x))$。

自编码器单独训练，单独的图片数据集即可训练完成。

扩散模型

这一段非常简单，先看看原始的扩散公式

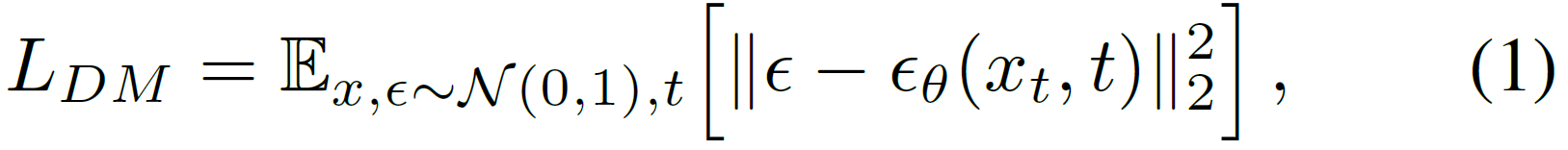
再看看潜空间版，区别一目了然

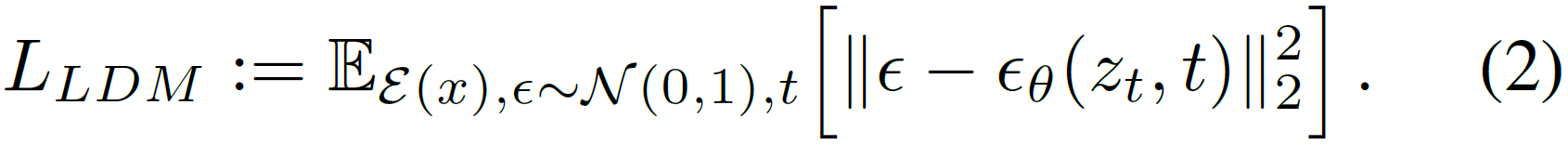
下面是一个训练过程中的示意图

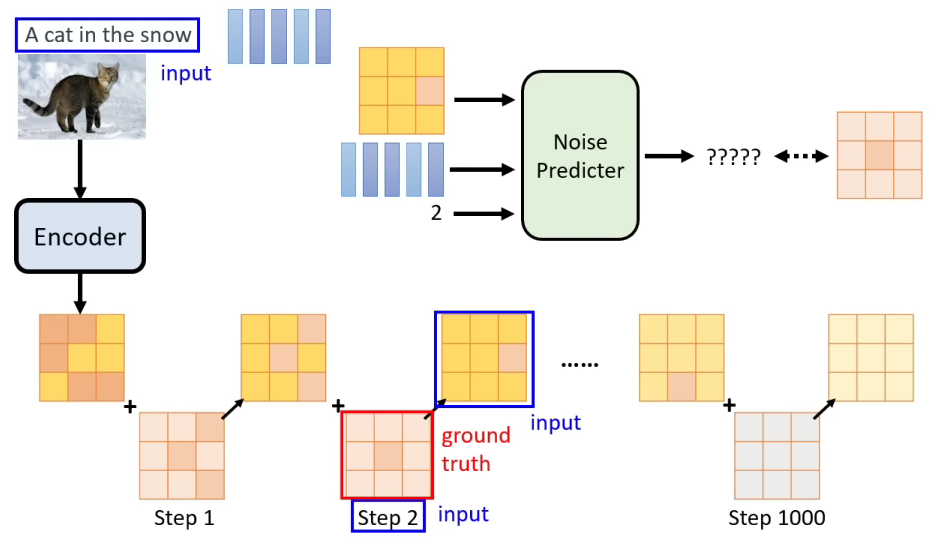
条件引导模型

所谓的条件引导，就是输入文字或者图片后，引导模型生成与之相关的图片，也就是文生图或图生图的过程。

如果将上述这些条件统一表述为$y$，那么去噪自编码器需要重写为条件去噪自编码器，即${ϵ}_{\theta }\left(z_t,t,y\right)$。

那这个条件如何作用呢？对于输入的条件$y$，使用域自适应的编码器${\tau }_{\theta }$得到其中间表示${\tau }_{\theta }(y)\in {\mathbb{R}}^{M\times d_{\tau }}$，再利用自注意力机制将其与UNet融合，其中${\phi }_i\left(z_t\right)\in {\mathbb{R}}^{N\times d_{ϵ}^i}$是UNet的中间层参数。

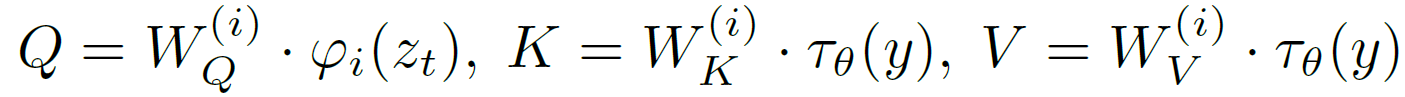
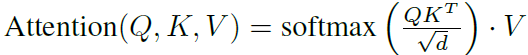
以Stable Diffusion为例，它使用下图所示的基于图文相似度配对而成的CLIP ViT-L/14 （PMLR2021论文：Learning Transferable Visual Models From Natural Language Supervision）作为文本编码器${\tau }_{\theta }$。这个编码器会将句子的长度限制为最大77个字符，如果长度超出，模型会对其进行截断。编码后输出的矩阵维度是77x768，其中768是隐藏层的大小。
如果输入条件包含图片，那么可以用自编码器中的编码器部分作为图片编码器${\tau }_{\theta }$。

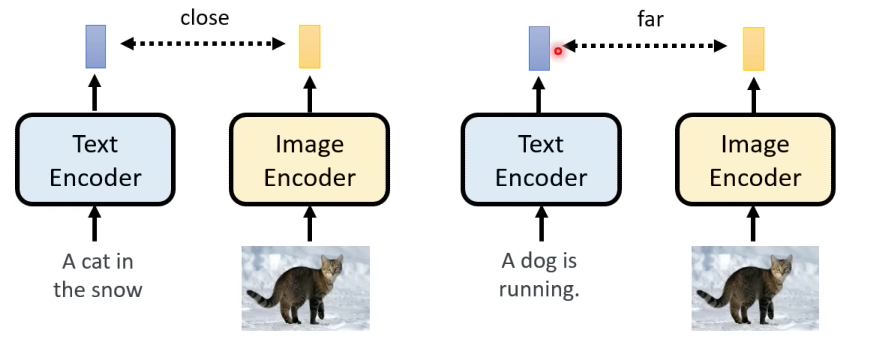
最终优化的目标函数如下，其中${\tau }_{\theta }$和${ϵ}_{\theta }$被联合优化

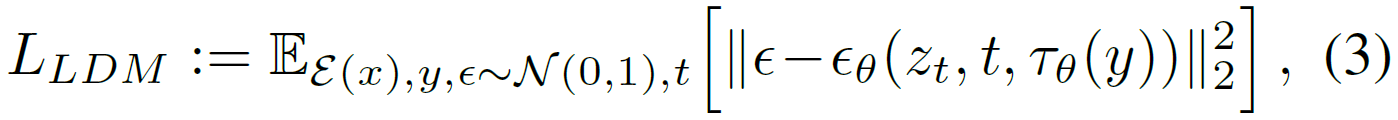
图像生成过程

在训练完成后，模型在隐空间随机产生一个噪音，与输入条件相结合，经过扩散过程去噪之后输入解码器，得到一张图像。

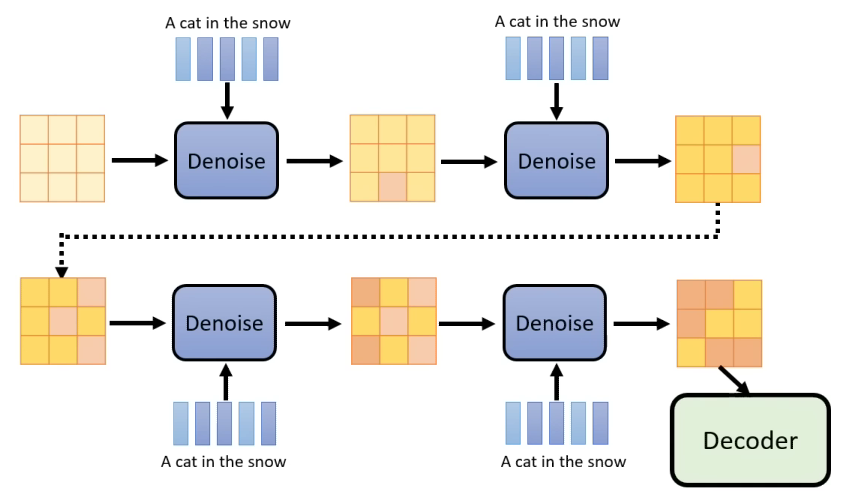
你可能会疑惑，为什么使用Stable Diffusion的时候，可以看到一个图片由模糊变清晰的过程呢？隐空间的表示难道不是肉眼不可见的吗？其实这很简单，让每一步去噪后的隐空间表示都由解码器处理一遍即可，但要注意并不是把它直接输入解码器，而是要通过上一章的扩散公式转换成隐空间的$z_0$表示，再输入解码器。

实验结果

指标定义

IS（越大越好）

nception Score（IS）是一个用于评估生成模型（如生成对抗网络GANs）性能的指标。它是由Tim Salimans等人于2016年在论文《Improved Techniques for Training GANs》中提出的。Inception Score的主要思想是使用一个预训练的Inception模型（通常是一个在ImageNet数据集上训练的深度卷积网络）来评估生成图像的质量和多样性。
Inception Score的计算步骤如下：

1. 分类概率：首先，将生成的图像输入到预训练的Inception模型中，得到每个图像属于ImageNet数据集中1000个类别的概率分布。

2. 图像质量：对于每个生成的图像，选择概率最高的类别，计算该类别的概率（即图像被正确分类的置信度）。这个过程反映了图像的质量，因为清晰的图像应该有一个高的最大概率。

3. 图像多样性：计算所有生成图像的平均分类概率的熵。熵越高，说明生成的图像属于不同类别的分布越均匀，即图像的多样性越好。

4. 综合评分：最后，将图像质量的指标和图像多样性的指标相乘，得到最终的Inception Score。公式可以表示为：

   $$IS=exp({\mathbb{E}}_x[D_{KL}(p(y|x)||p(y))])$$
   其中，$p(y|x)$ 是模型对图像$x$的分类概率分布，$p(y)$是所有图像的平均分类概率分布，$D_{KL}$是KL散度，用于衡量两个概率分布的差异。

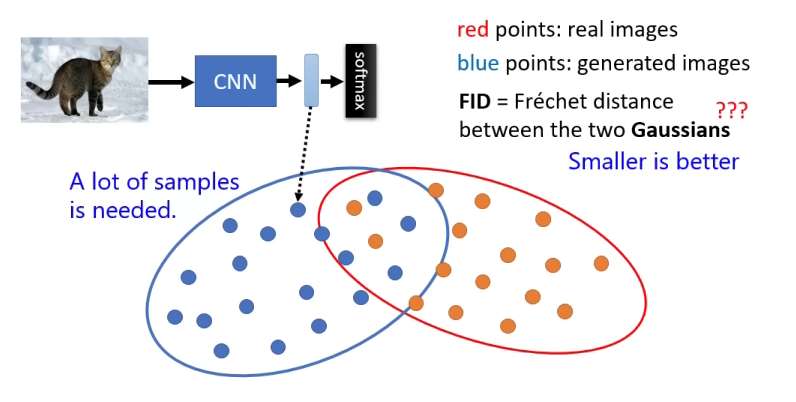
Inception Score的一个缺点是它主要关注图像的多样性，而不是图像的真实性。因此，即使生成的图像非常多样，但如果不真实，Inception Score也可能很高。为了解决这个问题，研究人员提出了其他指标，如Fréchet Inception Distance (FID)，它同时考虑了图像的质量和真实性。

FID（越小越好）

IFréchet Inception Distance (FID) 是一种用于评估生成模型（如生成对抗网络 GANs）生成图像质量的指标。FID 通过比较生成图像的特征分布与真实图像的特征分布之间的差异来衡量图像的真实性。FID 值越低，表明生成图像的质量越高，因为它们在特征空间中与真实图像更接近。
FID 的计算步骤如下：

1. 特征提取：首先，使用一个预训练的 Inception-v3 模型（通常在 ImageNet 数据集上训练）来提取图像的特征。这个模型在最后一个池化层之前有一个瓶颈层，可以输出一个 2048 维的特征向量。
2. 计算特征向量：对于一组真实图像和一组生成图像，分别计算它们通过 Inception-v3 模型得到的特征向量的平均值$\mu$和协方差矩阵$\Sigma$。
3. Fréchet 距离：然后，计算两个特征分布之间的 Fréchet 距离。这个距离是一个统计距离，用于衡量两个多元高斯分布之间的差异。Fréchet 距离定义为两个分布的均值之间的欧氏距离和它们协方差矩阵之间的加权几何距离的平方根。
   $$FID=\Vert {\mu }_1-{\mu }_2{\Vert }^2+Tr({\Sigma }_1+{\Sigma }_2-2({\Sigma }_1{\Sigma }_2{)}^{1/2})$$
   其中，${\mu }_1$和${\mu }_2$分别是真实图像和生成图像的特征向量的平均值，${\Sigma }_1$和${\Sigma }_2$是它们的协方差矩阵，$Tr$表示矩阵的迹。

FID 的优势在于它同时考虑了生成图像的多样性和真实性，因为它比较了整个特征分布而不是单个图像。FID 值低意味着生成图像不仅在视觉上接近真实图像，而且在统计上也非常相似。因此，FID 是评估 GANs 和其他生成模型性能的一个非常有用的工具，其示意图如下。

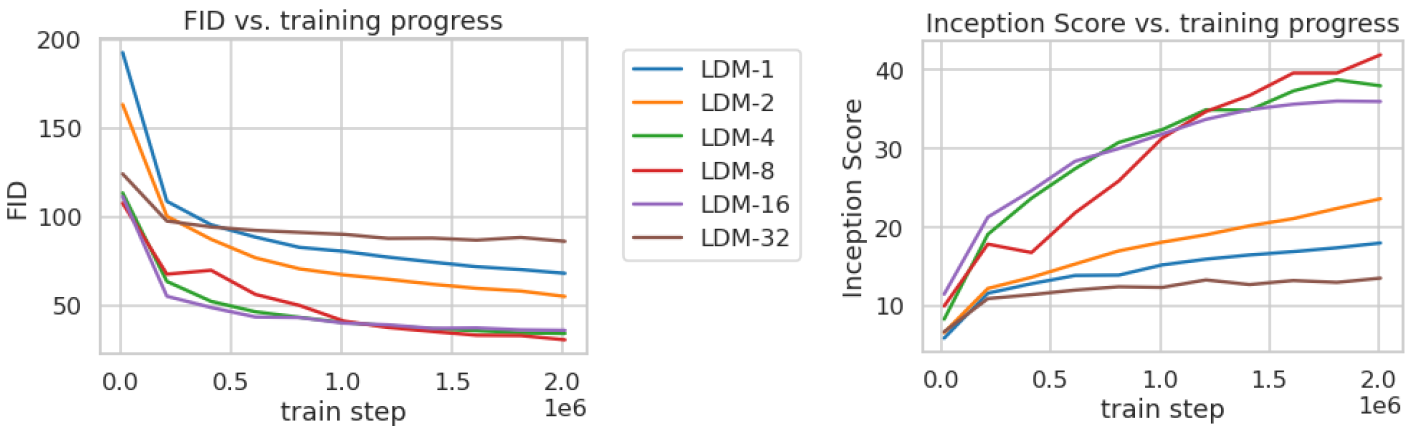
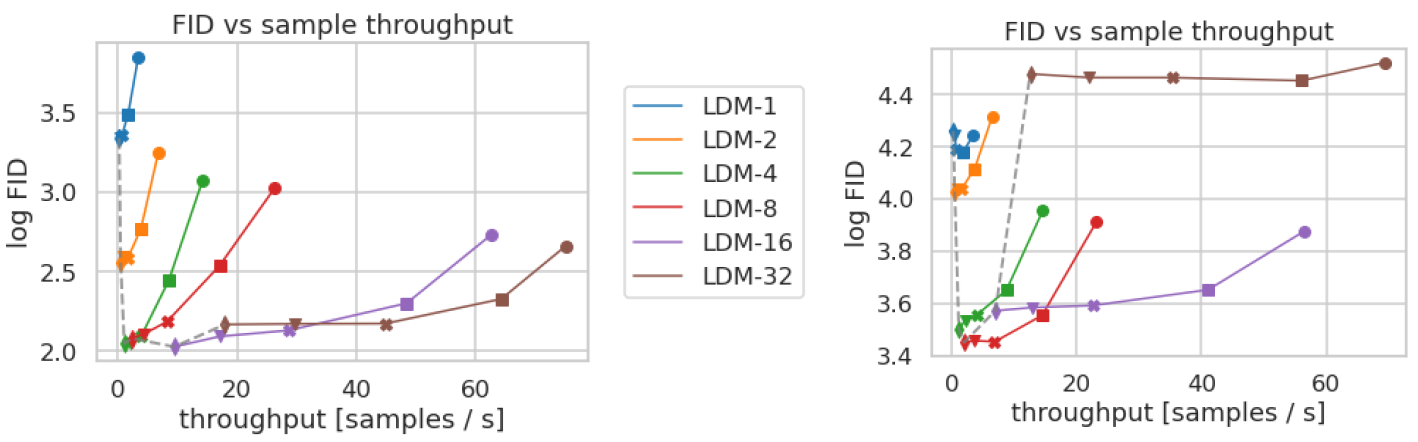
训练成本与采样质量分析

分析了不同降采样率$f$对模型训练成本和采样质量的影响。结果表明，LDM-4和LDM-8在下采样率与采样质量之间达到了平衡，训练成本低，采样质量高。

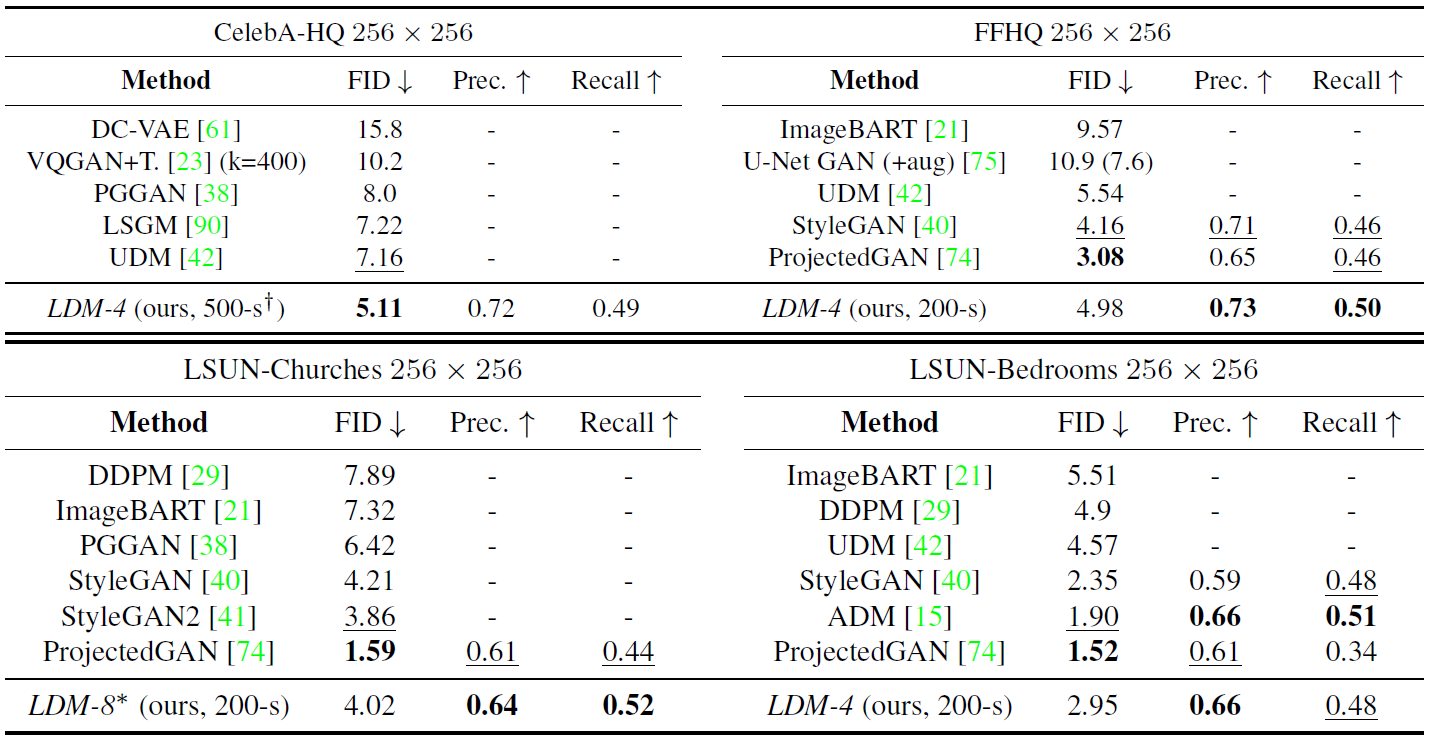
不带条件的图片生成

下面是降采样率为4的LCM模型在不同数据集上的生成指标和实际效果

基于文本的图片生成

论文中使用BERT-tokenizer和transformer作为文本域的${\tau }_{\theta }$，其指标和效果如下。

基于语义框的图片生成

使用来自OpenImages的带语义框标注的图像作为数据集训练，并在coco上微调。

基于语义图的图片生成

这一块的亮点主要在于它在生成图片时在分辨率上有泛化性，可以生成比训练分辨率更大的图片。

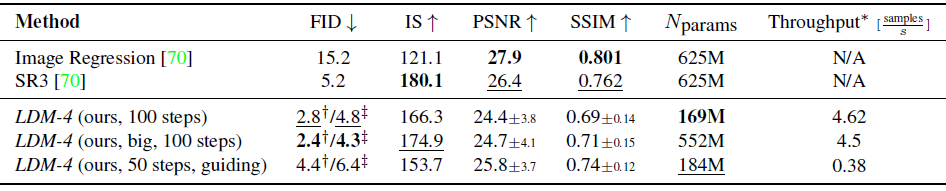
超分辨率图像生成

输入的是一个低分辨率图片，并且${\tau }_{\theta }$仅做了保持原状的操作，除了用指标，还使用了人为打分来评估效果。

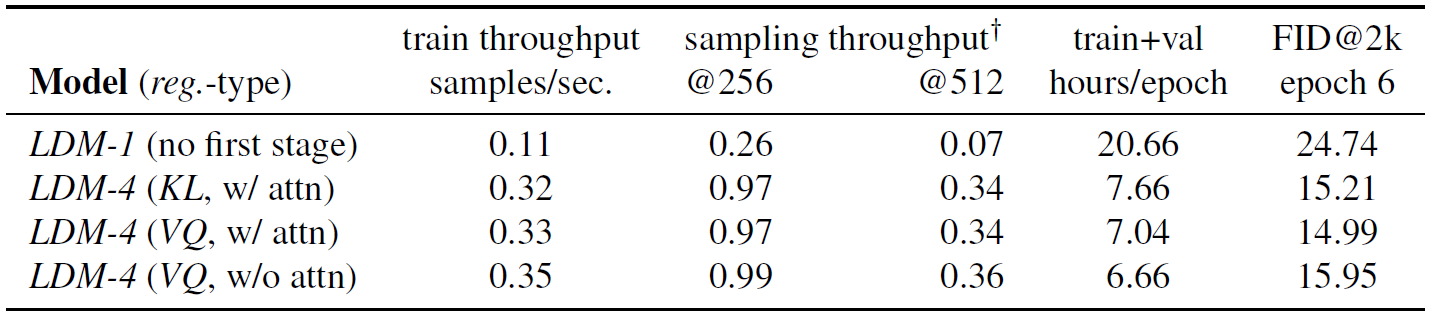
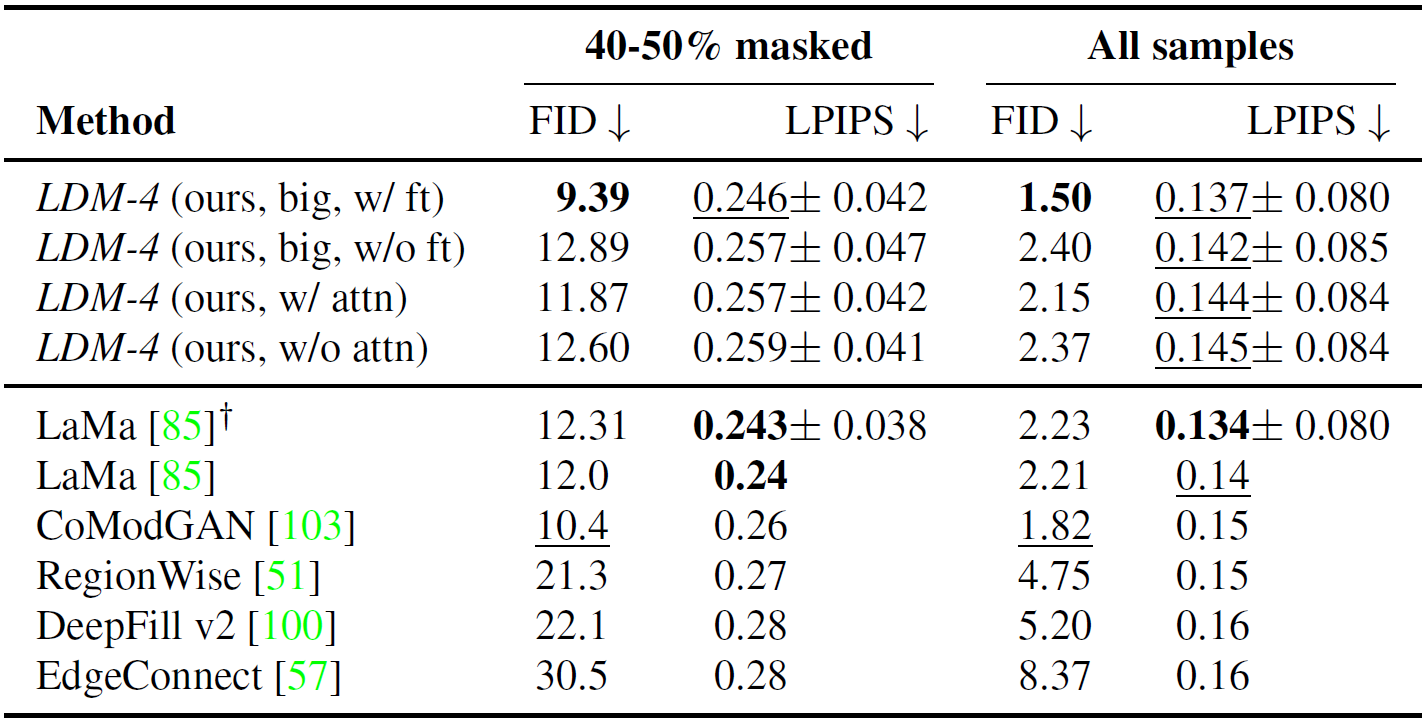
图像重绘

重绘任务（Inpainting task）通常指的是图像修复或图像补全的任务。这个任务的目标是填充或修复图像中的缺失部分，使得修复后的图像在视觉上尽可能自然和连贯。

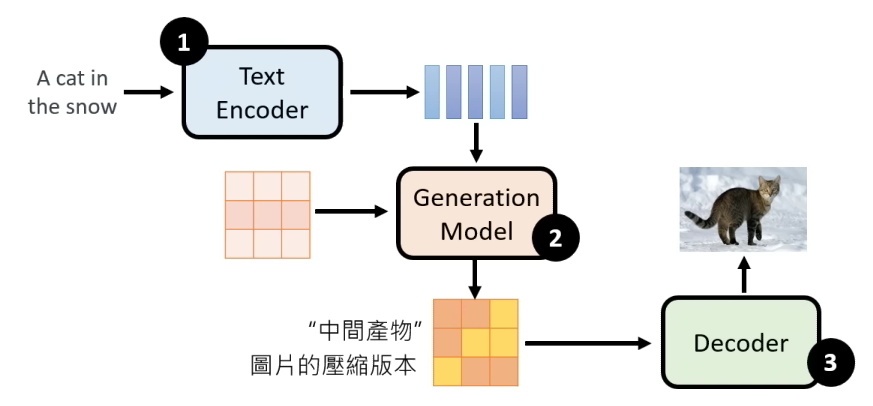
其他文生图模型

根据上面所解释的Stable Diffusion模型架构，其实可以抽象出文生图模型的通用结构，它包含三部分，一个是文本编码器，一个是从噪音开始的中间产物生成模型，一个是将中间产物映射回像素空间的解码器。下面就简单介绍一下其他文生图模型的结构。

DALL-E

DALL-E的名称是“DAL”和“E”的组合，其中“DAL”代表“扩散变换自回归解码器”（Diffusion Autoregressive Decoder），而“E”代表“变换器”（Encoder），这是DALL-E模型中使用的两种主要神经网络架构。

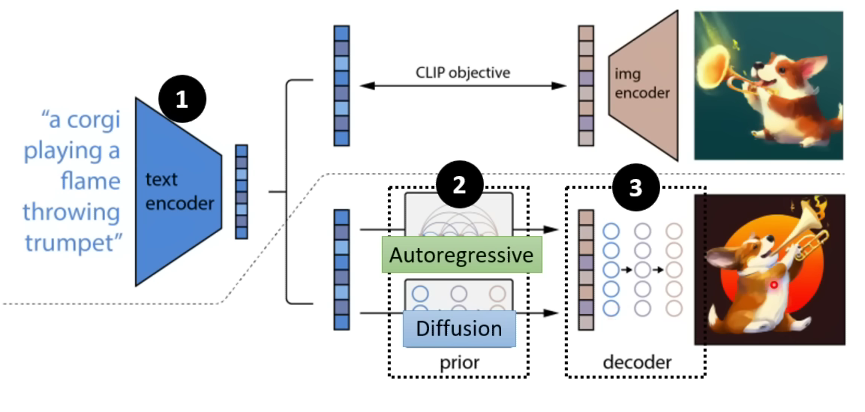
Imagen

Imagen是基于扩散模型（diffusion models）构建的，包括小图生成和大图上采样两步。