paper：Asymmetric Temperature Scaling Makes Larger Networks Teach Well Again

official implementation：https://gitee.com/mindspore/models/tree/master/research/cv/ats

本文的创新点

在知识蒸馏中，一个奇怪的现象是大的教师模型未必教的好，调整温度也无法缓解模型容量不匹配的问题。为了解释这个问题，本文将KD的作用分解为三个部分：correct guidance, smooth regularization, class discriminability。最后一点描述的是在蒸馏中教师模型提供的错误类别概率的区分性，大的教师模型往往会过度自信，传统的温度缩放限制了类别差异的作用，导致错误类别概率的区分度变小。因此，本文提出了不对称温度缩放Asymmetric Temperature Scaling (ATS)，对于正确和错误的类别分别应用较高和较低的温度，增大了教师模型预测中错误类别概率的方差，从而使学生模型尽可能的学习到错误类别与目标类别的绝对相关性。

方法介绍

通常蒸馏损失采用KL散度损失并与原本的交叉熵训练损失结合到一起，如下

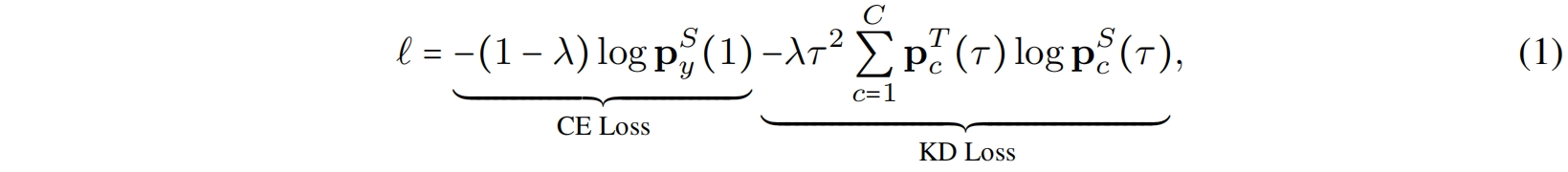
作者将式(1)中的 \(\lambda \tau ^{2}\) 去掉，并定义 \(e(\mathbf{q}^{T}(\tau))=\frac{1}{C-1} {\textstyle \sum_{j=1,j\ne y}^{C} \mathbf{p}^{T}_{j}(\tau) }\)，其中 \(\mathbf{q}^{T}(\tau)=\begin{bmatrix}
\mathbf{p}^{T}_{c}(\tau)
\end{bmatrix}_{c\ne y}\)，然后就得到了式(2)

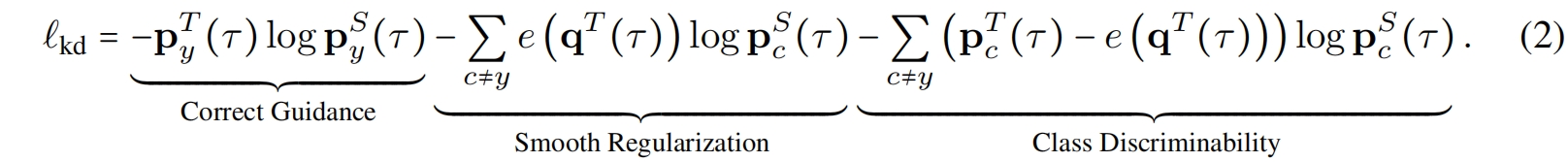
其中第三项class discriminability告诉学生错误类别与目标类别的关系，传递类别相关性给学生一直是KD中"dark knowledge"的主流猜测。理想情况下，一个好的教师应该尽可能有区分度的告诉学生哪些类别和目标类别更相关。

分解的图示如图1 Left，显然一个合适的temperature应该同时考虑到这三项的作用，过高或过低的温度导致更小的类别区分度，使得错误类别之间的差异变小，降低蒸馏的性能。

理论分析

Lemma 4.1 给定logit向量 \(\mathbf{f}\in \mathbb{R}^{C}\) 和softened概率向量 \(\mathbf{p}=SF(\mathbf{f};\tau),\tau \in(0,\infty)\)，\(v(\mathbf{p})\) 随着 \(\tau\) 的增大单调减小。但是我们更关注的是非目标类别，其中均值和方差可以更直观的计算和分析。 

Assumption 4.2 目标类别的logit比其它类别的logits大，这个假设是合理的，因为训练好的教师模型在训练集上的精度很高，且大多数训练样本都满足这一要求。

Proposition 4.3 在Assumption 4.2下 \(\mathbf{p}_{y}\) 随着 \(\tau\) 的增大单调减小，\(e(\mathbf{q})\) 随着 \(\tau\) 的增大单调增大，\(\tau \to \infty ,e(\mathbf{q})\to 1/C\)。这意味着温度越大，derived average越大，并增强式(2)中的smooth regularization。

在分析class discriminability项之前，先定义 \({\tilde{\mathbf{q}} } (\tau)\) 为在温度 \(\tau\) 下只对错误logits应用softmax的结果，即 \({\tilde{q} } (\tau)=SF(\mathbf{g};\tau)\)。对于 \(\mathbf{q}\) 的元素索引 \(c'\)，有

\({\tilde{\mathbf{q}} }\) 和 \(\mathbf{q}\) 不一样，前者满足 \( {\textstyle \sum_{c'}^{}}{\tilde{\mathbf{q}} }_{c'} =1\)，后者的和 \( {\textstyle \sum_{c\ne y}^{}}{\mathbf{p}}_{c} =1-\mathbf{p}_{y}\)，前者不依赖正确类别的logit而后者依赖。作者将 \(v(\tilde{\mathbf{q}})\) 称为 \(Inherent\; Variance(IV)\) 因为它依赖错误类别的logits。

Proposition 4.4 (Derived Variance vs. Inherent Variance) derived variance取决于derived average的平方和inherent variance

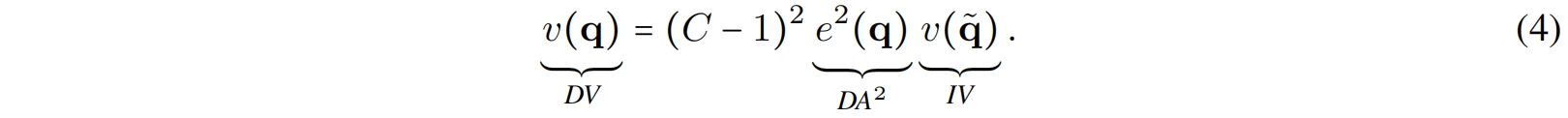
当 \(\tau\) 变大，\(e(\mathbf{q})\) 增大（Proposition 4.3）而 \(v(\tilde{\mathbf{q}})\) 减小（Lemma 4.1），因此不好判断 \(v(\mathbf{q})\) 相对于 \(\tau\) 的单调性。从图7可以看到derived variance先增大后减小，符合图1中所示的class discriminability的变化。

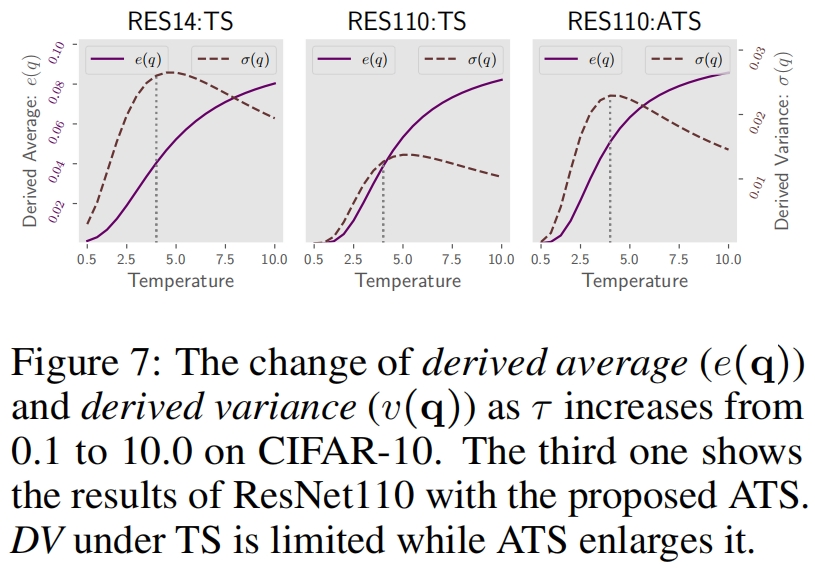
我们可以使用Proposition 4.4来清楚地分析为什么更大的教师无法教的更好。在这之前，我们再给出另外两个性质和一个推论

这个推论解释了为什么一个更大的老师不能更好地教学。因为更大的教师往往过于自信，目标logit \(\mathbf{f}_{y}\) 可能更大或错误logits的方差 \(v(\mathbf{g})\) 可能更小，这个结果如图1所示并在图4中进行了验证。

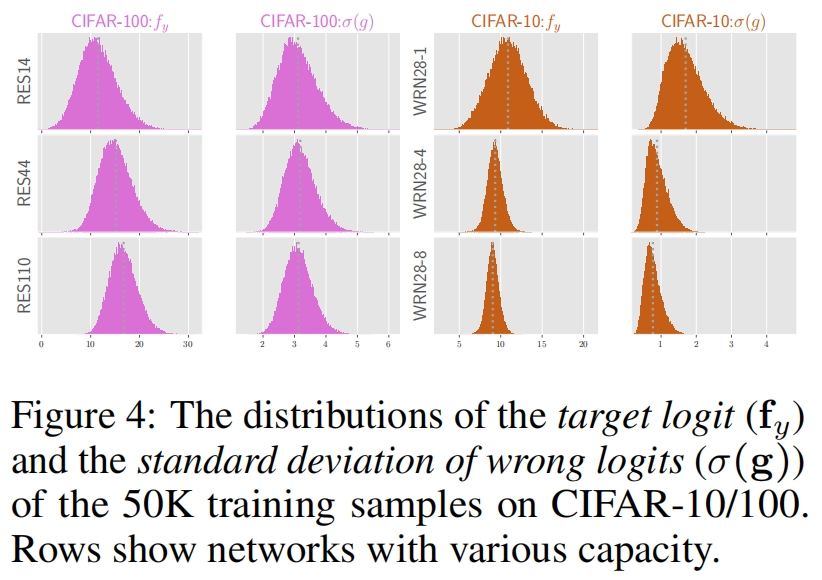
然后derived variance \(v(\mathbf{q})\) 可能变小，限制了式(2)中class discriminability的作用，验证结果如图(7)。

值得注意的是，作者专注于分析错误类概率的方差，而不是所有类。最大化所有类的概率的方差并不意味着最大化错误类的方差。例如，虽然一个非常低的温度可以最大限度地提高所有类别的概率的方差，但生成的教师标签是单一的，在错误类别之间没有区别。换句话说，KD的有效性应该更多地与错误类之间的差异相关，而不是所有类。然而，传统的温度缩放对所有类都采用统一的温度值，不能单独处理错误的类。

Asymmetric Temperature Scaling

我们得出上述分析：如果一个更大的老师做出了一个过度自信的预测，它提供的错误类别的概率可能没有足够的差异性。利用统一的温度并不能在目标类logit的干扰下（如图7的中间）尽可能地增大derived variance。好在根据式(2)中的分解，correct guidance项的作用类似于交叉熵损失，因此我们可以单独处理它。作者提出了一种新的温度缩放方法

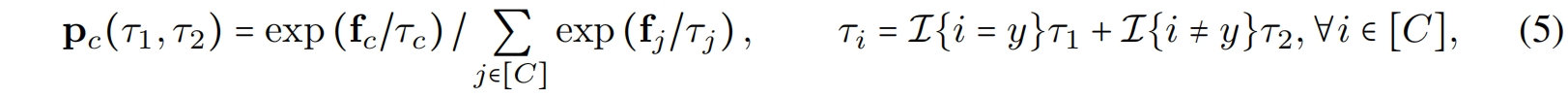
其中 \(\tau_{1}>\tau_{2}>0\)。这个方法叫做不对称温度缩放（ATS）因为对正确和错误类别的logits应用了不同的温度。根据式(4)当教师过于自信时ATS的作用如下

• 如果教师正确类别输出一个更大的logit \(\mathbf{f}_{y}\)，一个相对更大的 \(\tau_{1}\) 可以将其减小到一个合理的范围，即减小 \(\mathbf{p}_{y}\) 增大 \(e(\mathbf{q})\)，并最终增大derived variance \(v(\mathbf{q})\)
• 如果教师对所有错误类别输出变化较小的logits，一个相对较小的温度 \(\tau_{2}\) 可以使它们的差异更大，即增大 \(v(\tilde{\mathbf{q}})\)，最终增大derived variance \(v(\mathbf{q})\)

ATS在增大derived variance上更加灵活（如图7右所示），即它在教学时可以给出更差异化的蒸馏指导。

实验结果

以往的研究发现，精度更高的教师不一定教得好，如图9所示，尽管在{1.0, 2.0, 4.0, 8.0, 16.0}中调整了温度，更大的教师在传统温度缩放（实线）下的教学结果更差，但使用ATS（虚线）可以使更大的教师教的更好。