“任世界多宽广,停泊在这港口~”
区间问题,涉及到最多的就是 取交集 和 并集的概念。我们使用C++排序算法后,其默认规则就是按照 “左排序”进行的。因而,我们实质上注意的是每一个区间的 右端点,根据题目要求,总结规律,指定出策略解决问题。
合并区间
(1) 题目解析 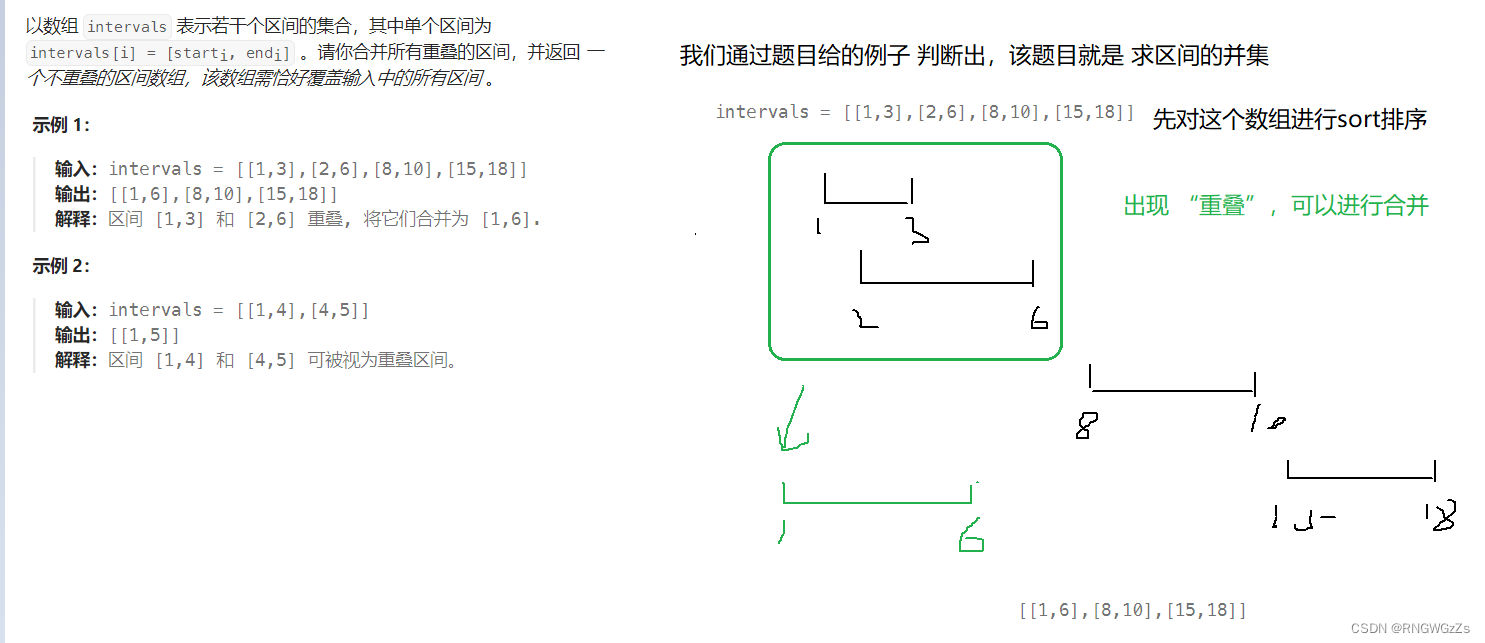
(2) 算法原理 
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(),intervals.end());
vector<vector<int>> res;
int n = intervals.size();
// 取左右端点
int left = intervals[0][0],right = intervals[0][1];
for(int i=1;i<n;++i)
{
int a = intervals[i][0],b = intervals[i][1];
if(a <= right){
// 有重合区间
right = max(right,b);
}
else
{
// 更新
res.push_back({left,right});
left = a;
right = b;
}
}
// 最后一组 区间 也需要被插入
res.push_back({left,right});
return res;
}
};证明:
因为,我们默认了排完序之后,所有的左端点,能合并的,都是连续的。所以,我们使用反证法设:左端点排完序后,不连续
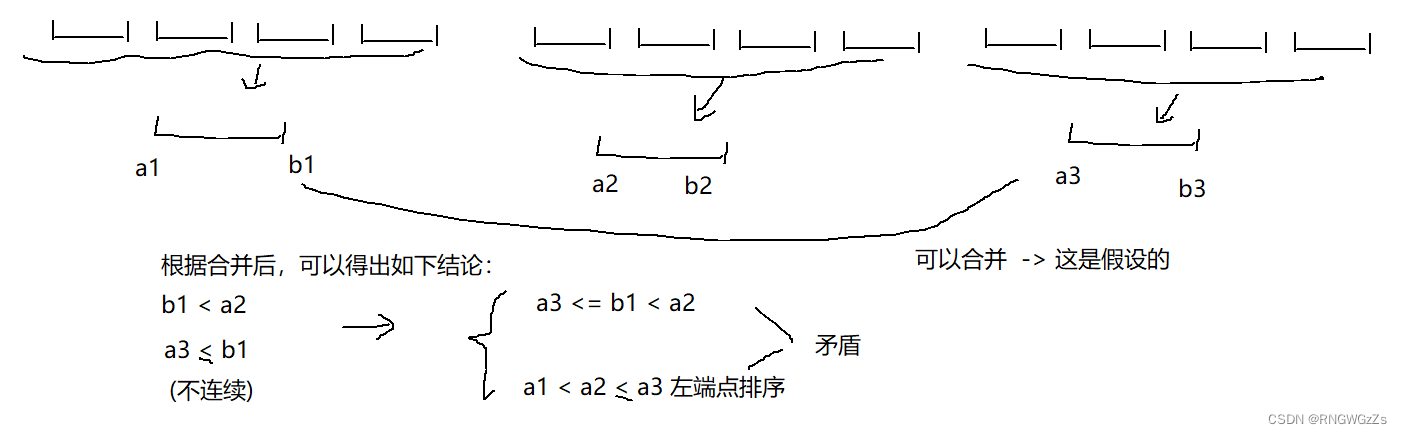
所以,我们按照左端点排完序后,一旦将区间合并,那么其一顶是连续的。
无重叠区间
(1) 题目解析
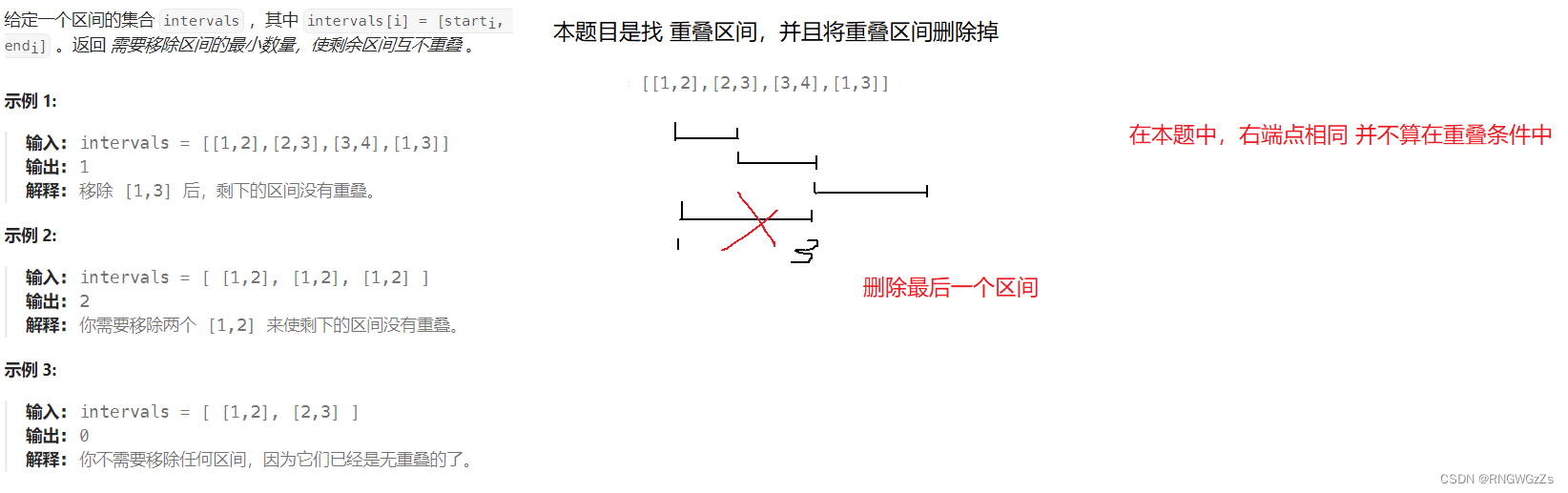
(2) 算法原理
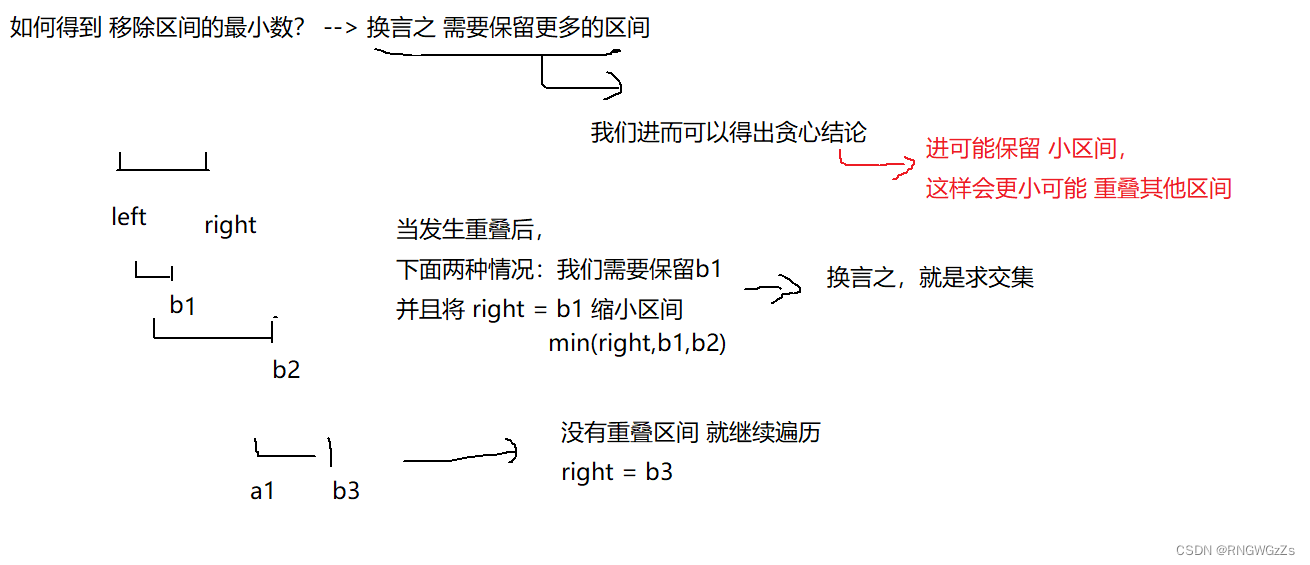
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
sort(intervals.begin(),intervals.end());
int n = intervals.size();
int ret = 0;
int left = intervals[0][0],right = intervals[0][1];
for(int i=1;i<n;++i){
int a = intervals[i][0],b = intervals[i][1];
if(a < right){
// 存在重叠 保留小范围的
ret++;
right = min(right,b);
}
else{
// 不存在重叠 新的开始
right = b;
}
}
return ret;
}
};证明:
这样的贪心策略是否正确呢 ?我们假设贪心解是错误的。所以,我们会得到两份答案,一份是贪心解,一份是最有解: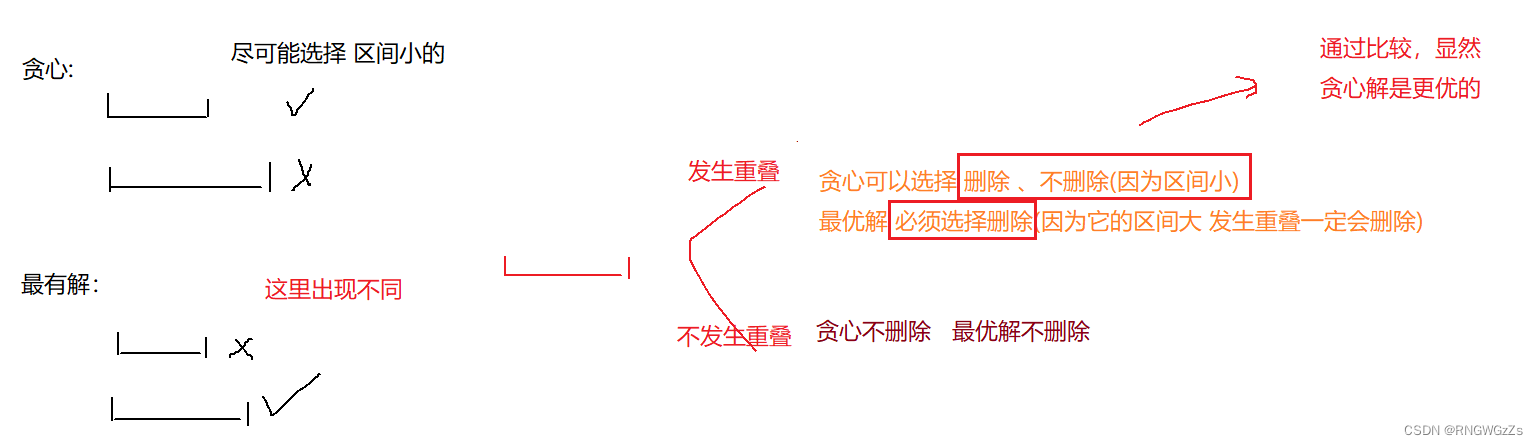
⽤最少数量的箭引爆⽓球
(1) 题目解析
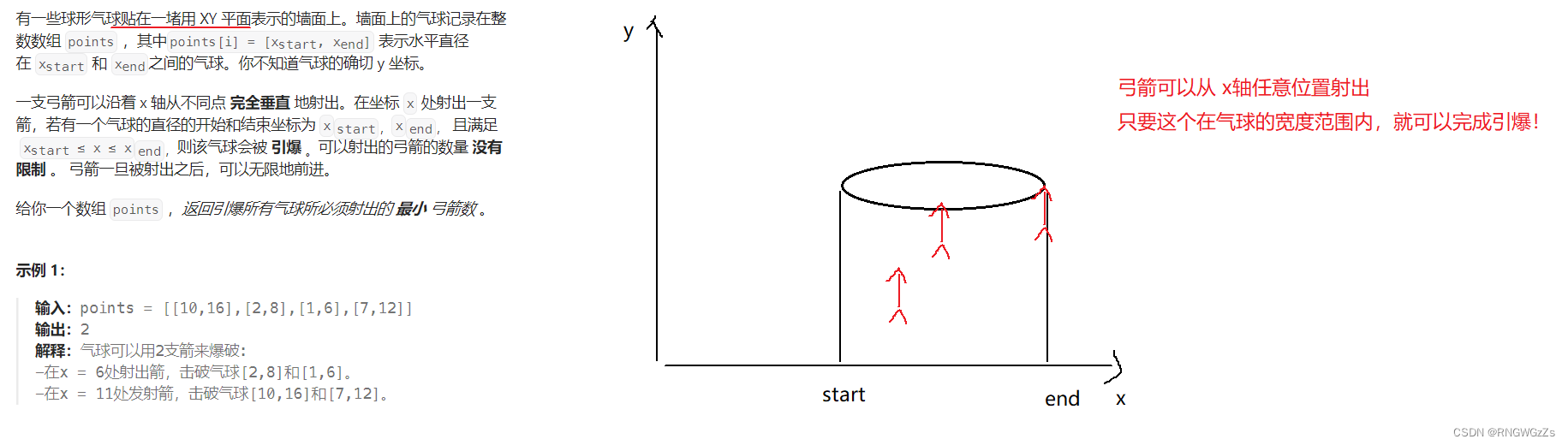
(2) 算法原理

class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(),points.end());
int n = points.size();
int left = points[0][0],right = points[0][1];
int ret = 1; // 第一个区间就需要引爆
for(int i=1;i<n;++i)
{
int a = points[i][0],b = points[i][1];
if(a <= right)
{
// 重叠的 可以一支箭引爆
right = min(right,b);
}
else
{
ret++; // 不是重叠 需要一支箭引爆
right = b;
}
}
return ret;
}
};本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~