基于Python3的数据结构与算法 - 01 复杂度和列表查找

news2025/1/17 3:55:33

一、时间复杂度

定义：用来评估算法运行效率的一个式子。

例如：此处的O(1) 详单与一个时间单位

接下来我们看下面两个式子：

如果按照上面的定义，那么打印三次相当O(3)，下面的循环相当于O(n2+1)

但是实际不是这样的

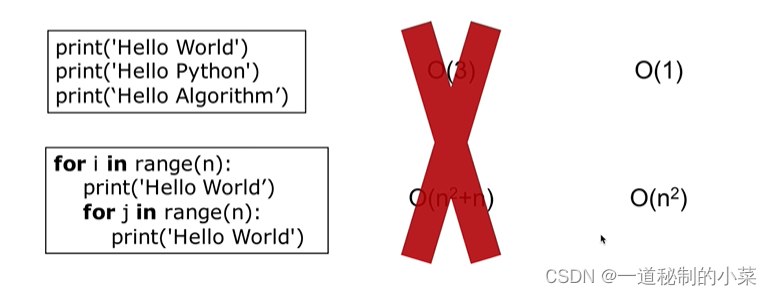
因为这里的时间单位并不是一个精确的时间单位，而是一个大概估计值；在计算机中，打印一次和打印三次的时间差不多；此处的时间复杂度对笔者自己而言有点类似于高数中的无穷小概念。

当算法中出现循环规模使得减半，一定会出现logn。

小结

时间复杂度是用来评估算法运行时间的一个式子（单位）。
一般来说，时间复杂度高的算法比复杂度低的算法慢。
常见的时间复杂度有：O(1)<O(logn)<O(n)<O(nlogn)<O( ${_{n}}^{2}$ )<O(n2logn)<O(n3)
复杂问题的时间复杂度：O(n!)O( ${_{2}}^{n}$ )O( ${_{n}}^{n}$ )...

快速判断算法复杂度（适用于绝大多数情况）：

确定问题规模n
循环减半过程→logn
k层关于n循环→ $^{{_{n}}^{k}}$
复杂情况：根据算法执行过程判断

二、空间复杂度

空间复杂度：用来评估算法内存占用大小的式子

空间复杂度的表示方法和时间复杂度完全一样

算法使用了几个变量：O(1)
算法使用了长度为n的一维列表：O(n)
算法使用了m行n列的二维列表：O(mn)

由于当前计算机硬件发展迅速，在写算法期间，我们采用“空间换时间”的方式。即时间的重要性大于空间。

三、递归

递归具有两个特点：

调用自身
结束条件

观察上面四个式子，我们发现：

func1(x)没有结束条件，所以不算递归；

func2(x)同样没有结束条件，所以不算递归；

func3(x)属于递归；假如传入x=3，打印3，2，1

func4(x)属于递归；假如传入x=3，打印1，2，3

四、汉诺塔问题

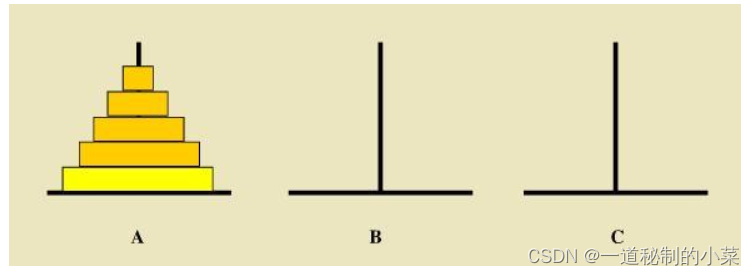
目的：把圆盘按大小顺序重新摆放到另一根柱子上。

要求：在小圆盘上不能放大圆盘；在三根柱子之间一次只能移动一个圆盘。

对于n个盘子是：

把n-1个圆盘从A经过C移动到B
把第n个圆盘从A移动到C
把n-1个小圆盘从B经过A移动到C

汉诺塔移动次数的递推式：h(n) = 2h(n-1)+1

可得h(64) = 18446744073709551615

如果婆罗门每秒钟搬一个盘子，则总共需要5800亿年。

示例代码如下：

def hanoi(n, a, b, c):  # 目的是经过b从a移动到c
    if n > 0:
        hanoi(n - 1, a, c, b)  # 第一步，把n-1个盘子从a经过c移动到b
        print("moving from %s to %s" % (a, c))  # 第二步，把第n个盘子从a移动到b
        hanoi(n - 1, b, a, c)  # 第三步，把n-1个盘子从b经过a移动到c


hanoi(3, "A", "B", "C")

输出结果如下：

输出结果即对应3层的汉诺塔操作步骤。

五、列表查找

查找：在一些数据元素中，通过一定的方法找出与给定关键字相同的数据元素的过程。

列表查找（线性表查找）：从列表中查找元素

输入：列标、待查找元素
输出：元素下标（未找到元素时一般返回None或-1）

内置列标查找函数：index()

1. 顺序查找

顺序查找：也叫线性查找，从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止。

def linear_search(li, val):  # li为一个列表；val为目标值
    for ind, v in enumerate(li):  # 遍历列表
        if v == val:  # 找到目标值
            return ind
    else:
        return None  # 未找到目标值

2. 二分查找(Binary Search)

二分查找：又叫折半查找，从有序列表的初始候选区li[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使后翔安区减少一半。（前提是有序列表；如果是无序列表，若只查找一次，还是采用线性查找较好；若需要查找n次，则先排序。再采样二分查找较好）

假如目前存在一个有序列表：

我们需要从列表中查找元素3：

设置两个变量：left和right
初始的时候：left=0；right=len(list)-1（列表第一个元素和最后一个元素）
求中间元素 mid=(left+right)/2 = 4 (索引)
因为mid>3;此时让right = mid-1 = 3（索引）
再计算新的mid比较目标值：mid = (left+right)/2 = 1.5 取1
mid = 2<3;此时让left = mid+1 = 2
此时只有两个值：left = 2; right = 3; mid = (left+right)/2 =2.5取2

示例代码如下：

def binary_search(li, val):
    left = 0
    right = len(li) - 1
    while left <= right:  # 候选去有数值
        # mid = int((left + right) / 2)
        mid = (left + right) // 2
        if li[mid] == val:
            return mid
        elif li[mid] > val:  # 待查找的值在mid左侧
            right = mid - 1
        else:
            left = mid + 1
    else:
        return None


li = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print(binary_search(li, 6))

因为二分查找每次使得候选区元素减半，因此时间复杂度为O(logn)。