文章目录
- 一、递归
- 二、尾递归
- 三、应用场景
- 参考文献
一、递归
递归(英语:Recursion)
在数学与计算机科学中,是指在函数的定义中使用函数自身的方法
在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数
其核心思想是把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解
一般来说,递归需要有边界条件、递归前进阶段和递归返回阶段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回
下面实现一个函数 pow(x, n),它可以计算x的n次方
使用迭代的方式,如下:
function pow(x, n) {
let result = 1;
// 再循环中,用 x 乘以 result n 次
for (let i = 0; i < n; i++) {
result *= x;
}
return result;
}
使用递归的方式,如下:
function pow(x, n) {
if (n == 1) {
return x;
} else {
return x * pow(x, n - 1);
}
}
pow(x, n) 被调用时,执行分为两个分支:
if n==1 = x
/
pow(x, n) =
\
else = x * pow(x, n - 1)
也就是说 pow 递归地调用自身 直到 n == 1
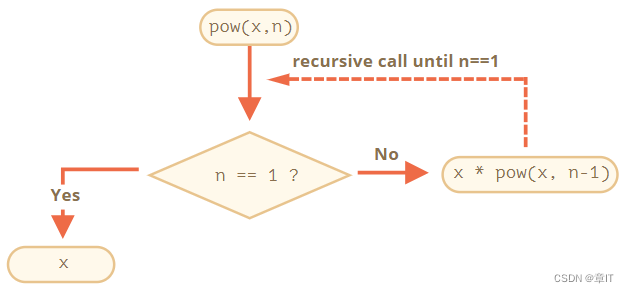
为了计算 pow(2, 4),递归变体经过了下面几个步骤:
1.pow(2, 4) = 2 * pow(2, 3)
2.pow(2, 3) = 2 * pow(2, 2)
3.pow(2, 2) = 2 * pow(2, 1)
4.pow(2, 1) = 2
因此,递归将函数调用简化为一个更简单的函数调用,然后再将其简化为一个更简单的函数,以此类推,直到结果
二、尾递归
尾递归,即在函数尾位置调用自身(或是一个尾调用本身的其他函数等等)。尾递归也是递归的一种特殊情形。尾递归是一种特殊的尾调用,即在尾部直接调用自身的递归函数
尾递归在普通尾调用的基础上,多出了2个特征:
- 在尾部调用的是函数自身
- 可通过优化,使得计算仅占用常量栈空间
在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储,递归次数过多容易造成栈溢出
这时候,我们就可以使用尾递归,即一个函数中所有递归形式的调用都出现在函数的末尾,对于尾递归来说,由于只存在一个调用记录,所以永远不会发生"栈溢出"错误
实现一下阶乘,如果用普通的递归,如下:
function factorial(n) {
if (n === 1) return 1;
return n * factorial(n - 1);
}
factorial(5) // 120
如果n等于5,这个方法要执行5次,才返回最终的计算表达式,这样每次都要保存这个方法,就容易造成栈溢出,复杂度为O(n)
如果我们使用尾递归,则如下:
function factorial(n, total) {
if (n === 1) return total;
return factorial(n - 1, n * total);
}
factorial(5, 1) // 120
可以看到,每一次返回的就是一个新的函数,不带上一个函数的参数,也就不需要储存上一个函数了。尾递归只需要保存一个调用栈,复杂度 O(1)
三、应用场景
数组求和
function sumArray(arr, total) {
if(arr.length === 1) {
return total
}
return sum(arr, total + arr.pop())
}
使用尾递归优化求斐波那契数列
function factorial2 (n, start = 1, total = 1) {
if(n <= 2){
return total
}
return factorial2 (n -1, total, total + start)
}
数组扁平化
let a = [1,2,3, [1,2,3, [1,2,3]]]
// 变成
let a = [1,2,3,1,2,3,1,2,3]
// 具体实现
function flat(arr = [], result = []) {
arr.forEach(v => {
if(Array.isArray(v)) {
result = result.concat(flat(v, []))
}else {
result.push(v)
}
})
return result
}
数组对象格式化
let obj = {
a: '1',
b: {
c: '2',
D: {
E: '3'
}
}
}
// 转化为如下:
let obj = {
a: '1',
b: {
c: '2',
d: {
e: '3'
}
}
}
// 代码实现
function keysLower(obj) {
let reg = new RegExp("([A-Z]+)", "g");
for (let key in obj) {
if (obj.hasOwnProperty(key)) {
let temp = obj[key];
if (reg.test(key.toString())) {
// 将修改后的属性名重新赋值给temp,并在对象obj内添加一个转换后的属性
temp = obj[key.replace(reg, function (result) {
return result.toLowerCase()
})] = obj[key];
// 将之前大写的键属性删除
delete obj[key];
}
// 如果属性是对象或者数组,重新执行函数
if (typeof temp === 'object' || Object.prototype.toString.call(temp) === '[object Array]') {
keysLower(temp);
}
}
}
return obj;
};
参考文献
- https://zh.wikipedia.org/wiki/%E5%B0%BE%E8%B0%83%E7%94%A8
希望本文能够对您有所帮助!如果您有任何问题或建议,请随时在评论区留言联系 章挨踢(章IT)
谢谢阅读!