讲解视频：可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。​

MATLAB教程新手入门篇（数学建模清风主讲，适合零基础同学观看）_哔哩哔哩_bilibili

节选自第3章：课后习题讲解中拓展的函数

在讲解第三章课后习题的过程中，我给大家拓展了一些讲义中没有介绍的新函数：

---

（12）meshgrid函数（★★★★☆）

meshgrid函数可以基于向量x和y中包含的坐标来返回二维网格坐标。

举个具体的例子帮助大家理解：假设x轴坐标上的取值是[0 1 2 3 4]，y轴坐标上的取值是[0 1 2 3]，现在请使用x轴坐标和y轴坐标共同创建下图所示的二维网格坐标：

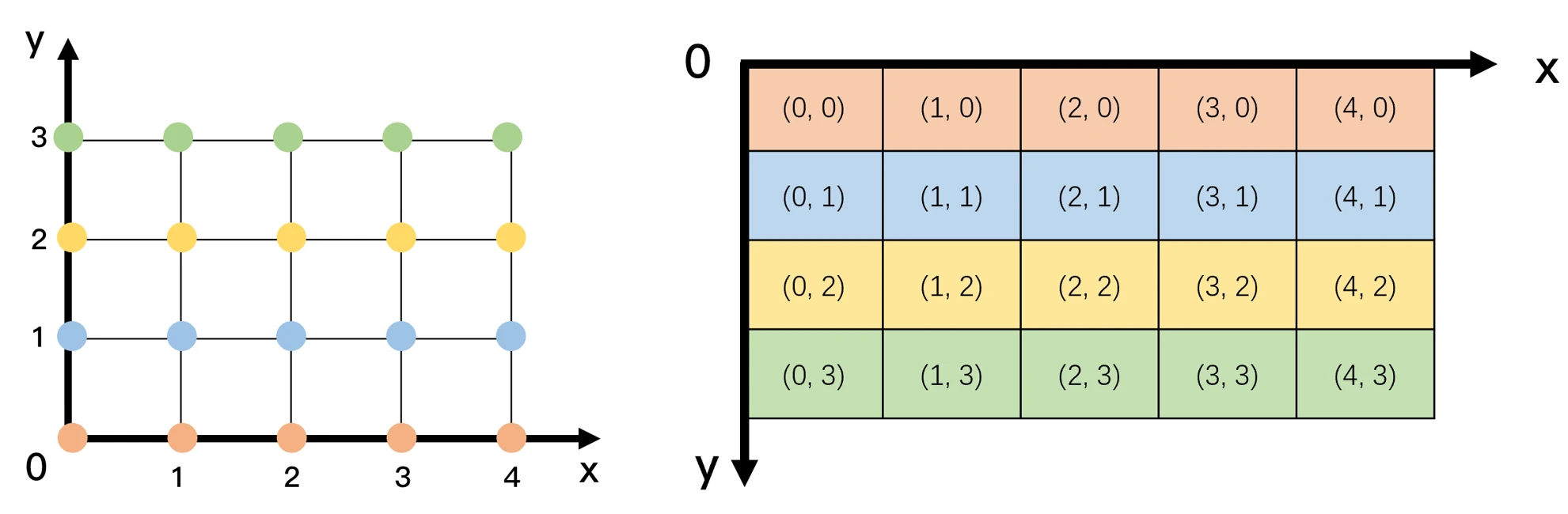
分析：x轴坐标上的取值有5种，y轴坐标上的取值有4种，将取值进行组合有20种，因此上方左图有20个交点，每个交点对应一个网格坐标。如果指定交点的排列顺序为沿着x轴的正方向和y轴的正方向，这样就能表示这20个交点的网格坐标，结果在上方右图中。

在MATLAB中，会将点的坐标(x, y)拆分成横坐标矩阵和纵坐标矩阵分别保存，我们可以使用meshgrid函数得到这两个矩阵：

进一步地，如果我们想在这20个交点构成的二维网格上计算二元函数的值，我们可以使用下面的代码：

另外，如果我们只给meshgrid函数一个输入变量，那么命令[X,Y] = meshgrid(x) 得到的结果和 [X,Y] = meshgrid(x,x)得到的结果完全相同。

事实上meshgrid函数在三维图的绘制中用的比较多，我们先给大家看个例子，后续章节中会系统讲解三维图的绘制方法。

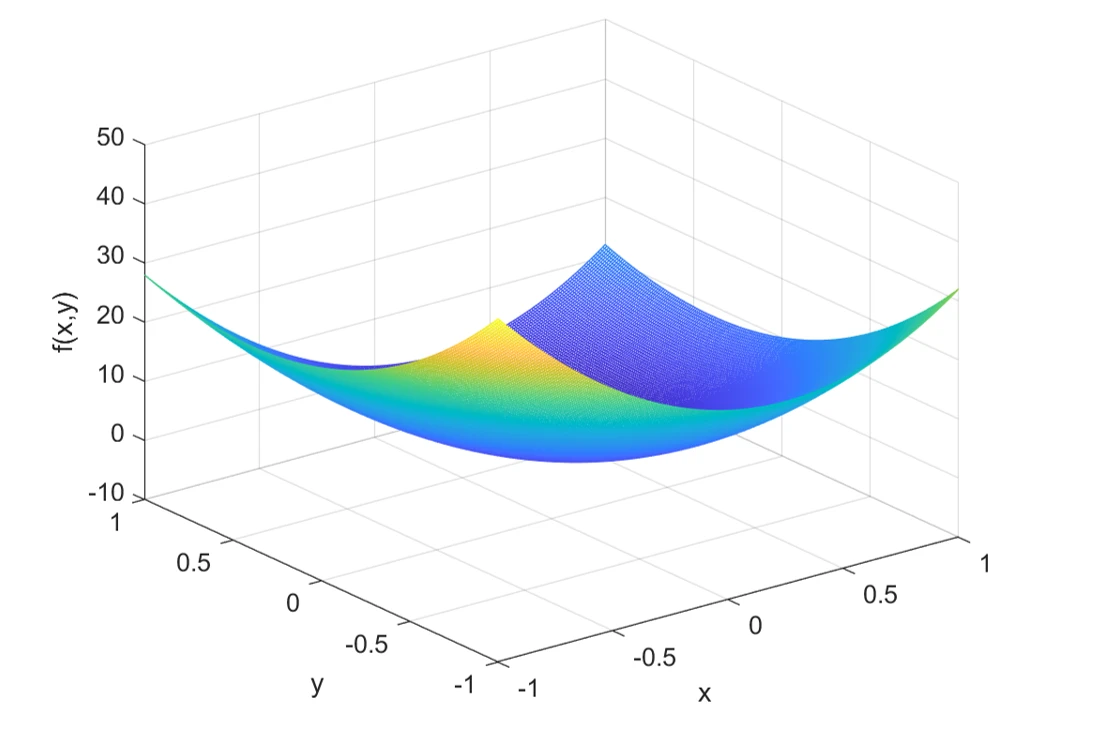
绘制  在𝑥和𝑦都位于区间[−1,1]上的图形。

d = 0.01;
x = -1:d:1;
y = -1:d:1;
[x,y] = meshgrid(x,y);  % 直接用meshgrid函数返回的x和y矩阵替换原来的输入变量x和y
z = x.^3 - y.^3 + 18 * x.^2 + 12 * y.^2 - 9 * x - 9 * y;
close all
mesh(x,y,z)  % mesh函数可用来绘制三维网格图，你也可以改成surf函数来绘制三维曲面图
xlabel('x');ylabel('y');zlabel('f(x,y)')