这两天在加强对最短路径的学习,除了Floyed比较简单之外,dijkstra、bell-mandford和SPFA学起来感觉有些难,洛谷上的模板题卡了半天都没写出来,最后只能通过看题解来帮助自己完成。
SPFA


算法实现:

最短路径算法对比比较:
| Floyed:时间复杂度O(N^3),适用于稠密图(和顶点关系密切),可以解决负权和处理负权边, 但是不能判定是否存在负权回路 |
| Dijkstra:时间复杂度O((M+N)logN),适用于稠密图(和顶点关系密切),不可以解决负权,不能处理负权边, 不能判定是否存在负权回路 |
| Bell-manford:时间复杂度O(NM),适用于稀疏图(和边关系密切),可以解决负权和处理负权边,可以判定 是否存在负权回路 |
| SPFA(队列优化的Bell-manford算法):时间复杂度O(NM)(最坏情况下),可以解决负权和处理负权边, 可以判定是否存在负权回路 |
| 一般情况下时间复杂度:Floyed>Dijkstra>Bell-manford>SPFA |
P3371 【模板】单源最短路径(弱化版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P3371 【模板】单源最短路径(弱化版)
题目背景
本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步 P4779。
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入格式
第一行包含三个整数 n,m,s,分别表示点的个数、有向边的个数、出发点的编号。
接下来 m 行每行包含三个整数 u,v,w,表示一条 u→v 的,长度为 w 的边。
输出格式
输出一行 n 个整数,第 i 个表示 s 到第 i 个点的最短路径,若不能到达则输出 2^31−1。
输入输出样例
输入
4 6 1 1 2 2 2 3 2 2 4 1 1 3 5 3 4 3 1 4 4
输出
0 2 4 3
说明/提示
【数据范围】
对于 20% 的数据:1≤n≤5,1≤m≤15;
对于 40% 的数据:1≤n≤100,1≤m≤10^4;
对于 70% 的数据:1≤n≤1000,1≤m≤10^5;
对于 100% 的数据:1≤n≤10^4,1≤m≤5×10^5,1≤u,v≤n,w≥0,∑w<2^31,保证数据随机。
Update 2022/07/29:两个点之间可能有多条边,敬请注意。
对于真正 100%100% 的数据,请移步 P4779![]() https://www.luogu.org/problemnew/show/P4779。请注意,该题与本题数据范围略有不同。
https://www.luogu.org/problemnew/show/P4779。请注意,该题与本题数据范围略有不同。
样例说明:
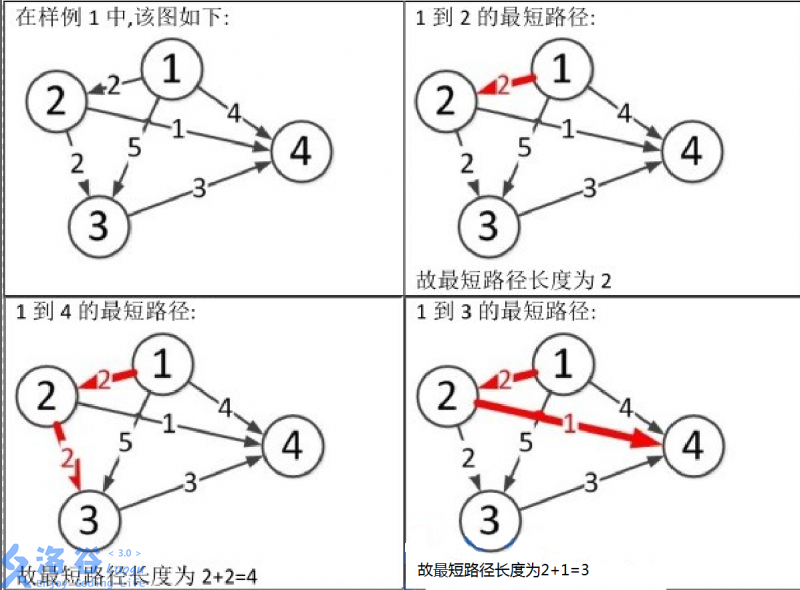
图片1到3和1到4的文字位置调换
对于这道题刚开始想用Floyed,发现怎么也过不了,后来转用Dijkstra,对于这个算法的使用也不是很会,只能套模板,搞了半天最后只好去看题解了
代码:
#include<bits/stdc++.h>
#include<iostream>
#include<math.h>
using namespace std;
const int inf=pow(2,31)-1;
int n , m , s ;
struct edge
{
int v , w;
};
vector<edge> e[500005];
int dis[100005] , pre[100005] ;
bool vis[100005] ;
int main()
{
cin>>n>>m>>s;
for(int i=0;i<=n;i++)
dis[i]=inf,vis[i]=false;
dis[s]=0;
for(int i=0;i<m;i++)
{
int u , v , w ;
cin>>u>>v>>w;
e[u].push_back({v,w});
}
for(int i=1;i<=n;i++){
int min_dis=inf , min_i=s;
for(int j=1;j<=n;j++){
if(vis[j]==0 && min_dis>dis[j]){
min_dis=dis[j];
min_i=j;
}
}
vis[min_i]=true;
for(int j=0;j<e[min_i].size();j++){
int y = e[min_i][j].v;
int d = e[min_i][j].w;
dis[y] = min(dis[y], dis[min_i] + d);
}
}
for(int i=1;i<=n;i++)
cout<<dis[i]<<" ";
}