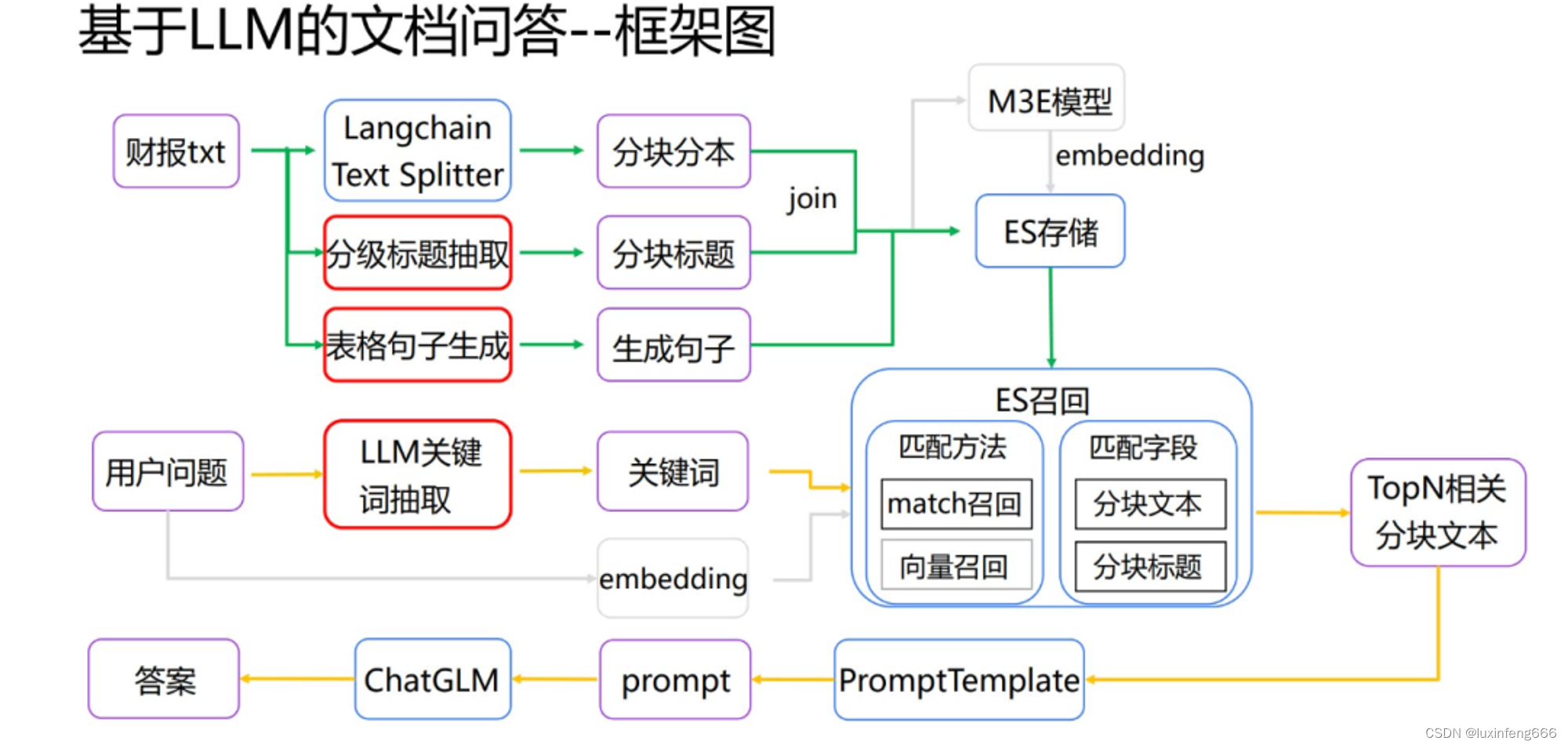
目录
前言
P1 - P8
监督学习
无监督学习
P9-P14
线性回归模型
成本(代价)函数
P15-P20
梯度下降
P21-P24
多类特征
向量化
多元线性回归的梯度下降
P25-P30
特征缩放
检查梯度下降是否收敛
学习率的选择
特征工程
多项式回归
前言
从今天开始,争取能够在开学之前(2.25)把b站上的【吴恩达机器学习】教程过一遍,并把笔记记录于此,本笔记将会把此课程每一p的重点内容及其截屏记录于此,以供大家参考和本人日后复习,课程链接如下:
吴恩达机器学习教程(bilibili)
推荐网站:
scikit-learn中文社区
吴恩达机器学习github资料
P1 - P8
生活中用到机器学习的例子:浏览器搜索、图片分类、手机语音助手、医疗诊断...
机器学习:一门在没有明确编程的情况下让计算机学习的科学
两种主要类型:监督学习(较多使用)、无监督学习
监督学习

监督学习(英语:Supervised learning),又叫有监督学习,监督式学习,是机器学习的一种方法,可以由训练资料中学到或建立一个模式(函数 / learning model),并依此模式推测新的实例。[1]训练资料是由输入对象(通常是向量)和预期输出所组成。函数的输出可以是一个连续的值(称为回归分析),或是预测一个分类标签(称作分类)
无监督学习

无监督学习(英语:unsupervised learning),又称非监督式学习,是机器学习的一种方法,没有给定事先标记过的训练示例,自动对输入的资料进行分类或分群。无监督学习的主要运用包含:聚类分析(cluster analysis)、关系规则(association rule)、维度缩减(dimensionality reduce)。它是监督式学习和强化学习等策略之外的一种选择。

无监督学习主要包含:聚类、异常检测、降维
P9-P14
线性回归模型

训练集:用于训练模型的数据集,包括输入特征(如房屋大小)和输出目标(如房屋价格),要训练模型就要将训练集提供给学习的算法

在机器学习中表示输入的标准符号是小写的x,称之为输入变量或特征、输入特征,小写y是输出变量、目标变量

对于线性回归模型,如何表示上述的function(或者说model)?

w、b是模型的参数,这是可以在训练期间调整以改进模型的变量,也被称为系数或权重
具有一个输入变量的线性模型的另一个名称是单变量线性回归(univariate linear regression)
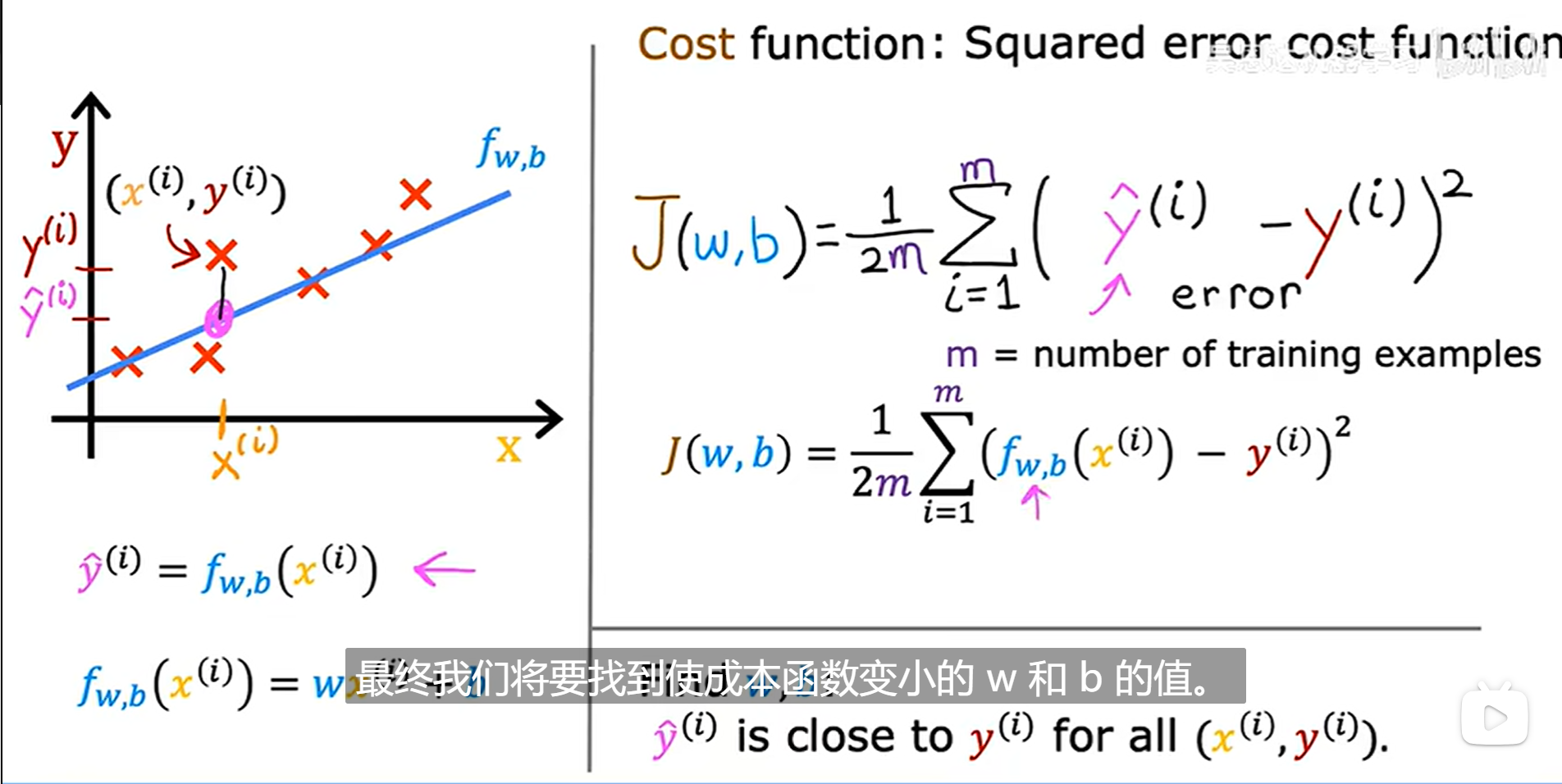
成本(代价)函数
成本函数采用预测y-hat并通过取y-hat减去y将其与目标y进行比较
平方误差成本函数(Squared error cost function):

如果把b一直设置为0,那么f(x)与J(w,b)的关系大概如下:

但若不忽略b,则损失函数的图像应该是三维,而非二维:

可以把f(x)和上面的损失函数进行结合:

对于右上边的图,是w和b的所有的取值情况(本质是J(w,b)中不同的函数值在wb平面上的投影),那么易知J最小的wb取值一定在同心圆的圆心处,此时读取wb值再在f(x)中画出此直线发现确实很适合训练集。
P15-P20
梯度下降
梯度下降在机器学习中无处不在,不仅用于线性回归,还用于训练一些最先进的神经网络模型(也称为深度学习模型),梯度下降适用于一般的函数,包括适用于具有两个以上参数的模型的其他成本函数


梯度下降算法:
其中“=”是赋值符号,α被称为学习率,通常是0到1之间的一个小正数,作用是控制下坡的步幅
另一个参数的处理同理:
此算法将会同理进行上述两个操作直到算法收敛,同理需要注意两个细节:
需要注意,要同时更新w和b,实现方法如下:

梯度下降的直观理解:

如果学习率太小,使得得到最小成本J的速度很慢
如果学习率太大,可能无法得到正确的最小成本J,如下所示:

如果已经位于局部最小值,那么梯度下降会使W保持不变:

回到线性回归中,通过微积分推导出它的梯度下降算法式子:

然后,将上述推导的结果插入梯度下降算法:

初始化参数w和b的位置不同,可能会使得梯度下降以不同的局部最小值结束,但事实证明,当使用线性回归的平方误差成本函数时,成本函数不会也永远不会有多个局部最小值
在线性回归中,运行梯度下降,便会出现下面的现象:

每一步的梯度下降使用所有的训练集叫做:批(batch)梯度下降
还有其它版本的梯度下降不会查看整个训练集,而是在每个更新步骤查看训练数据的较小子集
P21-P24
多类特征

引入向量之后,便可以把多元线性回归式写成如下形式:

向量化
使用向量化可以使代码更短,也使其运行更有效
下面是使用python中的numpy库进行非向量化和向量化的演示:

可以看出,使用向量化有两个好处:
1.使得代码更短
2.使得代码的运行速度更快(幕后原因是numpy函数能够在计算机中使用并行硬件,类似hpc)

多元线性回归的梯度下降

线性回归求w和b的另一种方法:正规方程法normal equation,只适用于线性回归、不需要进行迭代
其缺点是:
1.不能推广到其他学习算法,比如不能适用于logistic回归算法等
2.速度非常慢
我们不需要自己实现正规方程法,但是如果我们使用的一个成熟的机器学习库,并调用线性回归,有可能在后端,它将使用正规方程法求解w和b
P25-P30
特征缩放
特征缩放技术可以使梯度下降运行得更快
我们先讨论特征大小和参数值的联系:

如上图所示,当特征取值较大时,其对应的参数一般较小,在坐标中显示如下:

可以看出,x1是房子的尺寸取值从300到3000,而x2是卧室的数量,取值从0到5,导致参数w1、w2可取值的范围是右图所示的瘦高的椭圆,这就导致了一个问题:如果在某一个初始位置开始使用梯度下降算法,虽然会不断逼近椭圆中心,但是会来回左右反弹,导致总路途很长
如果此时,我们把x1、x2做一个特征缩放,那么椭圆形就会变成圆形,这时候,就可以直接通过最短的路径到达圆的中心!如下所示:

下面研究如何进行特征缩放
第一种最简单的方法就是让每一个特征除以特征的可能最大取值

除此之外还可以做均值归一化(mean normalization)

最后一种方法叫做Z分数归一化(Z-score normalization)

当变量(特征)范围太大、太小,或者本身的值与其它的变量差距过大,我们就可以考虑使用特征的缩放

检查梯度下降是否收敛
第一种方法是自行绘制损失函数的值与迭代次数的关系图,这个曲线应该一直下降,最后趋于平稳,若某一次迭代曲线突然增长说明代码有bug或者学习率α偏大,不同的应用程序需要的迭代次数可能相差很大。
还有一种方法是自动检测方法,我们可以设置一个很小的阈值epsilon,当某一次迭代之后曲线降低的值小于这个
,就说明到达了收敛,也就意味着找到了参数接近损失函数的全局最小值。
然而的值是很难确定的,所以一般倾向于第一种方法

学习率的选择
如下图所示,如果损失函数-迭代次数这个学习曲线出现了上下浮动或者持续增大的现象(如上面的两幅图片),说明代码存在bug或者学习率过大。
如下面的第一幅图所示,如果学习率过大,可能会导致不收敛的情况。此外,如果代码中有bug,比如更新参数的时候减号写成了加号,便会导致学习曲线的增长。
常用的一种判断是bug还是学习率过大的方法是:使用一个非常小的学习率,如果成本依然不会在每次迭代中减小,说明代码存在bug,需要注意的是这个非常小的学习率并不是最终的学习率的选择,而是代码的一种调试策略。

所以,当我们运行梯度下降时,可以尝试学习速率阿尔法一系列值,在学习曲线正常的前提下,尽量增大阿尔法值:

特征工程
特征的选择对于学习算法的性能产生巨大的影响,如何设计适合算法的特征?
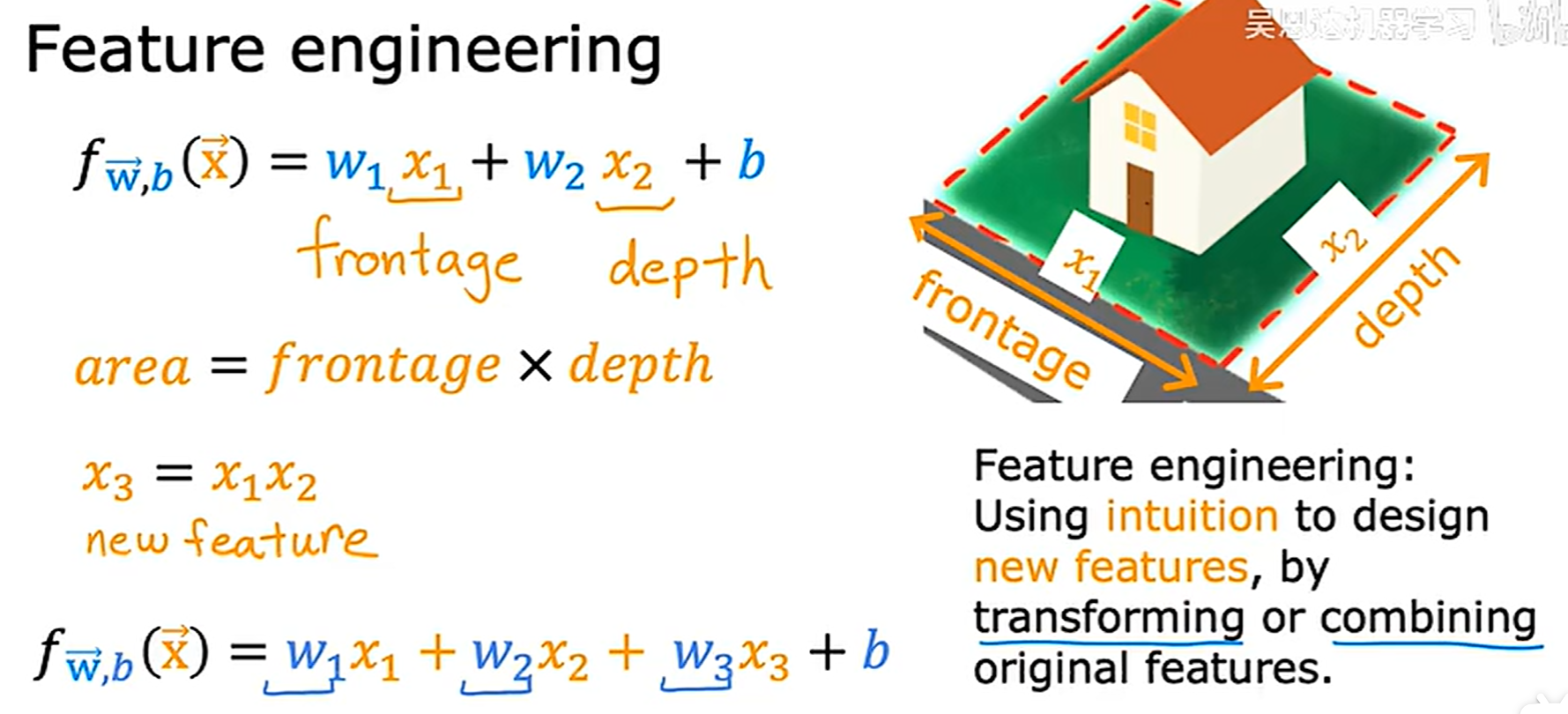
多项式回归


对于多项式回归,特征缩放变得更加重要