目录

一，3033. 修改矩阵

二，3035. 回文字符串的最大数量

三，3036. 匹配模式数组的子数组数目 II

---

一，3033. 修改矩阵

 这道题直接暴力求解，先算出每一列的最大值，再将所有为-1的区域替换成该列的最大值，代码如下：

class Solution {
    public int[][] modifiedMatrix(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[] max = new int[m];
        for(int j=0; j<m; j++){
            for(int i=0; i<n; i++){//得到每列的最大值
                max[j] = Math.max(max[j],matrix[i][j]);
            }
        }
        for(int i=0; i<n; i++){
            for(int j=0; j<m; j++){
               if(matrix[i][j] == -1){//是-1就进行替换
                   matrix[i][j] = max[j];
               }
            }
        }
        return matrix;
    }
}

二，3035. 回文字符串的最大数量

​

 这道题是问我们：怎样交换可以使words数组包含最大数量的回文串，注意只要输出回文串的最大数量。再仔细看题就会发现，这些数组中字符都是可以相互交换的，也就是说，我们可以先使用hash或者int[26]（题目说了只包含小写字母）来统计一下words数组中包含哪些字符及其对应的数目，再自己构造出固定长度的回文字符串。

这时还有一个问题，就是如何保证我们构造的字符串的数目一定是最大的，这里我们就要使用贪心的思想了，我们可以先得到words数组中字符串的长度，并将其从小到大排序，再根据长度从小到大来构造回文字符串，这样就可以保证构造出的回文字符串的数目是最大的。

其实再进一步想一想，回文字符串的特点是什么？不就是对称吗，也就是说我们根本不需要知道各个字符的数量，只需要知道，有多少成对的字符（使用two代替），又有多少单个字符（使用one来代替）。

大体思路想好了，剩下的就是如何构造字符串（假设我们要构造长度为x的回文字符串）：

 1）剩下的字符可以构造出字符串， 即 two - x/2 >= 0 && one - x%2 >= 0，同时ans++

2）剩下的字符不可以构造出字符串: 

1. 缺少成对的字符， 这时直接返回，因为我们是从小到大来构造字符串的，如果这个构造的字符串缺少成对的字符，那么后面的也一定缺少，即 two - x/2 < 0
2. 缺少单个字符，即 one - x%2 < 0， 这时候我们要看two是否还多余，如果多余，我们可以从two中拿出一个，同时ans++ (注意：当我们从two中拿出一个时，我们的one也要同时+1，相当于是将一个成对的字符拆成单个字符来使用)，如果缺少，直接返回。

进阶：上述讨论的2.2这种情况真的存在吗？

• 我们这样想一想，当答案就等于words.length的时候，two是最大的，one是最小的，而当one是最小的时候，他也能满足单个字符的需求，也就是说，我们不需要关心one，只需要关心two，即 two - x/2 >= 0 或者  two - x/2 < 0，当 >= 0 时， ans++；当 < 0 时，直接返回答案。

上代码：

class Solution {
    public int maxPalindromesAfterOperations(String[] words) {

        int[] m = new int[26];//统计各个字符出现的次数
        int[] t = new int[words.length];//统计words数组中字符串的长度
        for(int i=0; i<words.length; i++){
            t[i] = words[i].length(); 
            for(char ch : words[i].toCharArray()){
                m[ch-'a']++;
            }
        }

        Arrays.sort(t);//从小到大排序
        int two = 0;//统计成对字符的数目
        for(int i=0; i<26; i++){
            two += m[i]/2;
        }

        int ans = 0;
        for(int x : t){//从小到大构造回文字符串
            if(two-x/2>=0){
                two -= x/2;
                ans++;
            }else{
                return ans;
            }
        }

        return ans;    
    }
}

三，3036. 匹配模式数组的子数组数目 II

   

 这周周赛的二四题是相同的，这里就一起讲了。

该题的关键点在于是否能将这道题转换成一个 "字符串匹配" 问题：

我们通过题目给的条件：

•  nums[i] - nums[i-1] > 0，t[i-1] = 1 
• nums[i] - nums[i-1] == 0, t[i-1] = 0
• nums[i] - nums[i-1] < 0, t[i-1] = -1

可以得到一个 int[] t = new int[nums.length-1] 的数组，然后通过kmp算法求数组 t 中有多少和数组pattern相同的字数组。 

 代码如下：

class Solution {
    public int countMatchingSubarrays(int[] nums, int[] pattern) {
        int n = nums.length;
        int[] t = new int[n-1];
        for(int i=1; i<n; i++){
            if(nums[i]-nums[i-1]==0)
                t[i-1] = 0;
            else if(nums[i]-nums[i-1]>0)
                t[i-1] = 1;
            else 
                t[i-1] = -1;
        }
        //求next数组
        int k = pattern.length;
        int[] next = new int[k];
        for(int i=1, j=0; i<k; i++){
            while(j>0&&pattern[i]!=pattern[j]){
                j = next[j-1];
            }
            if(pattern[i]==pattern[j])
                j++;
            next[i] = j;
        }
        //字符串匹配
        int ans = 0;
        for(int i=0, j=0; i<n-1; i++){
            while(j>0&&j<k&&t[i]!=pattern[j]){
                j = next[j-1];
            }
            if(t[i]==pattern[j])
                j++;
            if(j==k){
                j = next[j-1];
                ans++;
            }
        }

        return ans;
    }
}

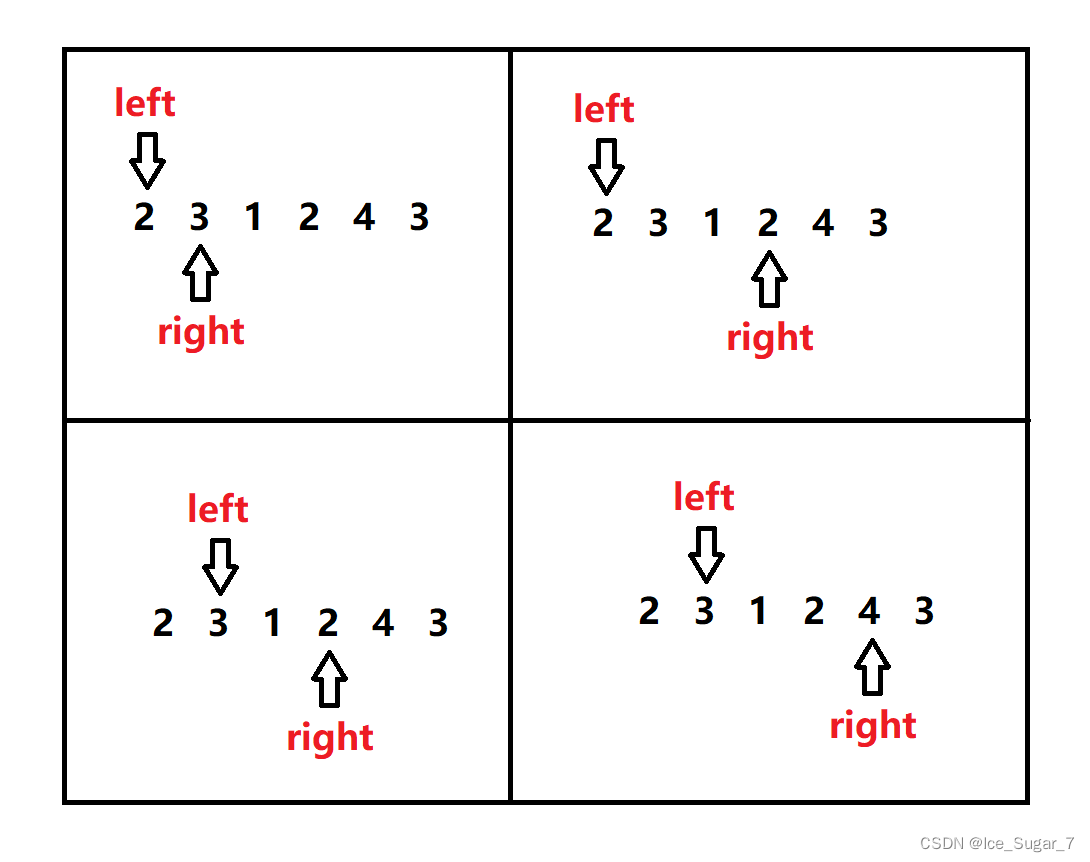
除了KMP算法之外，还可以通过Z函数算法来求解，下面简单来讲一讲Z函数算法的思想：和KMP的思路差不多，只不过kmp中的 next 数组是用来求字符串中的最长前后缀，而Z函数中的 z 数组则是用来求字符串的最长前前缀，举一个例子：

    

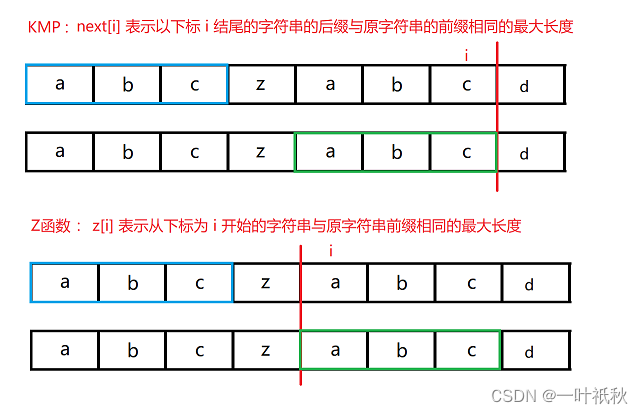
 使用该方法麻烦的点是：需要手动的将 pattern 数组添加到 t 数组的前面，然后只需要统计 z[i] （i >= pattern.length）大于等于 pattern.length 的数目就行了。

class Solution {
    public int countMatchingSubarrays(int[] nums, int[] pattern) {
        int n = nums.length;
        int[] t = new int[n-1];
        for(int i=1; i<n; i++){
            if(nums[i]-nums[i-1]==0)
                t[i-1] = 0;
            else if(nums[i]-nums[i-1]>0)
                t[i-1] = 1;
            else 
                t[i-1] = -1;
        }

        List<Integer> ls = new ArrayList<>();
        for(int x : pattern) ls.add(x);
        for(int x : t) ls.add(x);

        int ans = 0;
        int k = pattern.length;
        int[] z = new int[ls.size()];
        int l=0, r=0;
        for(int i=1; i<ls.size(); i++){
            if(i <= r)
                z[i] = Math.min(z[i-l], r-i+1);
            while(i+z[i]<ls.size() && ls.get(z[i]) == ls.get(i+z[i])){
                l = i;
                r = i + z[i];
                z[i]++;
            }
            if(i>=k && z[i]>=k) 
                ans++;
        }
        return ans;
    }
}