「算法」滑动窗口

news2024/11/23 3:16:48

前言

算法需要多刷题积累经验，所以我行文重心在于分析解题思路，理论知识部分会相对简略一些

正文

滑动窗口属于双指针，这两个指针是同向前行，它们所夹的区间就称为“窗口”

啥时候用滑动窗口？

题目涉及到“子序列”、“子数组”、“子串”等概念，要你求和它们相关的量，比如求满足条件的子数组的最大长度
在暴力枚举的时候，如果发现两个“指针”都是朝同一个方向走的，就可以考虑滑动窗口
注：滑动窗口可以看作是暴力枚举优化后的结果

如何使用？（步骤）

定义两个“指针”left、right（此“指针”不是真正的指针）
通过移动 right 让元素进窗口
进窗口之后进行判断，并根据这个判断决定什么时候需要出窗口

2和3需要放在一个循环里面，这样才可以让窗口不断往前走

在移动“窗口”的过程我们需要不断更新结果，比如求子数组最大长度maxLen，那么每次求出一个子数组长度之后，我们就要判断是否需要更新maxLen
至于是在进窗口后更新结果，还是在出窗口后更新，这就需要结合具体题目分析

例题

长度最小的子数组

思路：

先用暴力枚举看看怎么做，我们先固定一个端点left，然后让right一直往右走，直到[left,right]区间中的元素和大于target，此时得到区间长度为right-left+1
既然已经比target大，那接下来就别让right往右走了，先让它停下来，因为数组中全是正数，此时right继续走的话，区间中元素总和肯定还是比target大，但是此时区间的长度肯定不是最小长度，这样就做了无用功
所以我们应该让left向前走，缩小区间，将新区间的元素和与 target 比较，若大于 target，则记录此时区间长度，并让 left 继续向前走；反之则让 right 往前走

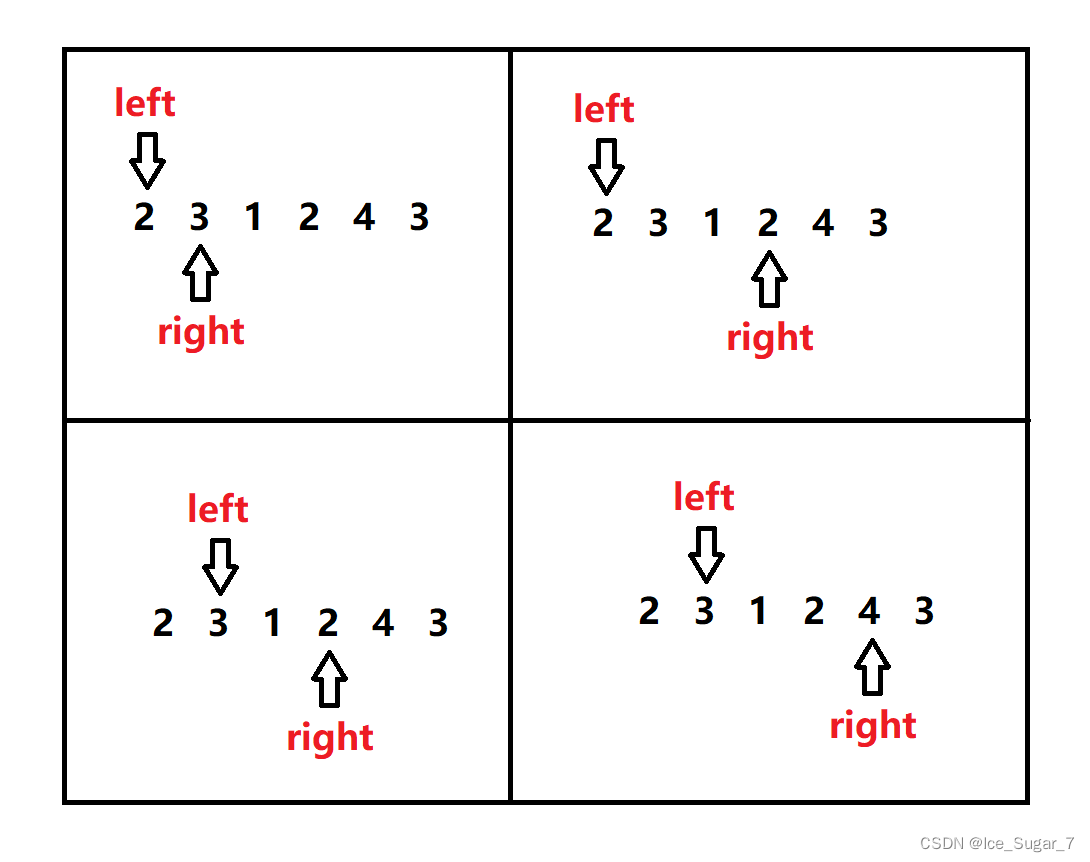
在这里插入图片描述

上面的思路其实就是从暴力枚举逐步过渡到滑动窗口，整个过程下来，我们不难发现：砍掉暴力枚举中那些无用功，也就得到滑动窗口的思路了

代码如下：

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0,right = 0;  //区间为左闭右闭
        int sum = 0;  //区间中元素总和
        int minLen = nums.length+1;  //最小窗口的长度，一开始初始化为一个比较大的数，不然下面使用取小函数可能没法正确更新minLen
        for(;right < nums.length;right++) {
            sum += nums[right];
            while(sum >= target) {
                minLen = Math.min(minLen,right-left+1);  //更新 minLen
                sum -= nums[left];
                left++;
            }
        }
        
    	return minLen == nums.length+1 ? 0 : minLen;
    }
}