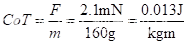神经网络漫谈(一)

发表时间： 2023年1月6日	创作地点：湖北省武汉市	作者：ixy_com&Bill Kromydas

封面图片来源：Towards Data Science

1、背景

基本概念：神经网络，也称为人工神经网络 (ANN) 或模拟神经网络 (SNN)，是机器学习的子集，并且是深度学习算法的核心。其名称和结构是受人类大脑的启发，模仿了生物神经元信号相互传递的方式。

人工神经网络 (ANN) 由节点层组成，包含一个输入层、一个或多个隐藏层和一个输出层。 每个节点也称为一个人工神经元，它们连接到另一个节点，具有相关的权重和阈值。 如果任何单个节点的输出高于指定的阈值，那么该节点将被激活，并将数据发送到网络的下一层。 否则，不会将数据传递到网络的下一层。

​ ---- IBM中国

---

内容说明：在这篇文章中，我将简要介绍训练神经网络所需的基本组件和概念，仅用于组内科普之用，不涉及相关复杂的数学概念。其中，以图像分类任务(如图1所示)为例展开相关内容的介绍。本文基本目标为：说明如何利用带标记数据进行建模、如何利用损失函数来对模型输入与预测输出之间的误差进行量化、如何利用梯度下降优化方法对网络权重进行更新。全文内容包含以下部分：

图 1-1 图像分类示意图

内容目录：

• 带有标记的训练数据(Train Data)和独热编码(One-Hot Encoding)
• 损失函数(Loss Function)
• 梯度下降(Gradient Descent)
• 权重更新(Weight Update)
• 权重更新示例(Sample)
• 完整的训练过程(Training)
• 模型推理(Model Inference)

2、正文

2.1 带标记的训练数据和独热编码

作为有监督机器学习的典型任务之一，图像分类任务的训练数据是带有标签(Labeled，或称为标记)的输入数据。具体地，带标记的训练数据(Labeled Training Data)由目标图像(Target Images)及其相应的真实标记(Ground Truth)组成。以进行三种图像类别分类的神经网络为例，训练数据的标签可能是cats、Dogs、others。为了实现分类任务，我们需要构建包含有上述所有三个类别的训练样本(Samples)，且常规的样本容量可能至少是几千张图像。

然而，在利用神经网络处理数据集之前，训练样本的标签须具有数值形式的编码表示。如下表所示，该种类型的标签编码称为整数编码。

表2-1 整数编码

Label	Description
0	cats
1	Dogs
2	others

但很明显，这种编码方式会引入标签之间的数值大小关系；因此，一种常用的编码技术为独热编码。在本示例中，我们有三个不同的类别，因此可以使用长度为3的向量分别对相应的标签进行编码表示，如下表所示：

表2-2独热编码

cats	Dogs	Others
1	0	0
0	1	0
0	0	1

以下图以单个样本为例，其由输入图像和与其对应的类别标签组成。对于每个输入到模型的训练样本，网络模型将预测得到一个预测结果，该预测结果由三个数组组成，用于代表输入图像属于特定类别的概率(或称为置信度)。其中，概率最高的输出便决定了模型对输入图像的标签预测。如图所示，模型预测结果中最大值为0.5，则对应于表2所示的独热编码，即可得知，模型错误地将输入图像分类为狗。

图2-2图像分类过程示意

2.2 损失函数

如上图1所示，模型在图像分类过程中出现了误判，那如何对模型分类准确与否进行量化评估？一种直接的思路是对模型预测结果(Predicted)和真实标签(Ground Truth)之间的误差进行量化，并经该量化过程用以数据公式进行表征，即得到损失函数。暂不对分类和回归任务做本质上的区分，为了更好的说明“误差量化”过程，这里采用误差平方和(Sum of the Squared Errors, SSE)进行说明。在本案例中，SSE计算如下：
$$SSE=(1-0.37{)}^2+(\mathrm{0.0.50}{)}^2+(0-0.13{)}^2=0.6638\text{\hspace{1em}(式1)}$$
在实际的模型训练过程中，对于模型的分类误差通常结合样本容量(即所有样本的条数)进行训练，其目的是计算得到模型在所有样本上的平均误差。因此在(式1)的基础上，通常采用均方误差(mean-square error, MSE)来计算损失。其计算过程如下：
$$MSE=\frac{1}{N}\sum _{i=1}^N(y_i-\widehat{(y_i)}{)}^2\text{\hspace{1em}(式2)}$$

2.3 梯度下降

如(式2)所示，其对应的函数图像为一个下凸函数。因此，结合函数极值的概念，我们需要求得当函数值最小时对应的模型权重，常用的方式为求导。对于光滑的函数，其满足极值点导函数为零。幸运的是，在机器学习理论中，常用于调整模型权重的方式于此原理契合，但正式的叫法为梯度下降。如下图所示：

图2-3 梯度下降示意

如图，纵轴为损失函数$Loss$的值，图中函数图像为下凸形状，简称为凸函数(注意区分高数中的凹函数定义，这里是学科定义差异)。我们知道，梯度方向是函数变化(增大)最快方向，则结合上图，为了求得$LOSS$最小时对应的权重$W$，需要调整调整权重至函数最低点，此时函数$LOSS$的变化方向为负梯度方向，如下图所示：

图2-4 负梯度方向示意

如图，该点的斜率计算过程为函数在$Y$轴的变化除以$X$轴自变量的变化。则，为了得到更优胜的权重值$W_{e2}$，我们需要将权重的取值沿$X$轴的正向移动，对应于函数图像的负梯度方向。如下图所示：

图2-5 权重更新示意

在实践中，我们需要设置一个超参数用于控制权重$W$的运动幅度，该超参数称为学习率(Learning rate, LR)，且取值通常小于1。

2.4 权重更新示例

为了更具体地说明上一节中的权重更新过程，这里用一个计算示例进行说明。假设当前权重$W_{e1}$取值为0.38，学习率为0.01，损失函数$LOSS$在点$W_{e1}$处的斜率为-0.55。则使用上图所示的计算过程，我们计算得到权重值$W_{e2}$为0.3855。具体如下图所示：

图2-6 权重更新示例

2.5 完整的训练过程

到此为止，我们已经以具体的一个样本为例，实现了一次模型训练。其中，模型训练过程是涉及到模型参数学习与模型超参数调整的过程。结合本示例，模型权重的更新过程为模型的参数学习过程，模型学习率的调整为模型的超参数调整过程，而后者取决于人工经验，更准确来讲，其不包含于模型训练过程。更具体地，完整的神经网络训练过程如下图所示：

图2-7 训练过程示意

2.6 模型推理

如上述小节所述，模型在完整的训练过程中对关键参数不断地学习更新，从而缩小预测结果与真实结果之间的误差。通常评估该误差的方式为绘制学习曲线(Learning Curve)，如下图所示。具体地，如果我们现在训练得到一个分类性能优异的图像分类模型，我们就可以使用该模型对未知的图像进行分类，则使用该模型进行未知图像分类的过程，我们称之为推理(Inference)。该推理过程，不需要任何的带标记数据，且模型在该未知数据上的分类能力，我们称之为泛化能力(Generalization ability)。

图2-8 学习曲线

图2-9 模型推理

3、全文总结(Conclusion)

至此，本次数字智能部的科普交流到此结束。此时，我们基本了解了神经网络的学习过程以及模型构建所需的基本组件。但我们尚尚未涉及到代码实战部门。后续内容，将持续更新到神经网络漫谈的专栏。回归本文，相关内容总结如下：

• 对于图像分类等有监督的学习任务，我们需要使用充足的带标记数据以训练模型。
• 一般情况下，对于分类任务的数据，我们可以使用one-hot对类别标签进行编码。
• 对于模型预测误差的量化，我们使用到的概念为损失函数。
• 对于损失函数的计算，一种更为便捷的方式是使用深度学习框架，如Pytorch、Tensorflow以及PaddlePaddle等。
• 神经网络模型权重更新的过程通常基于梯度下降优化算法。
• 在一个epoch的训练过程中，iterations数量等于训练样本数除以batch_size。
  于损失函数的计算，一种更为便捷的方式是使用深度学习框架，如Pytorch、Tensorflow以及PaddlePaddle等。
• 神经网络模型权重更新的过程通常基于梯度下降优化算法。
• 在一个epoch的训练过程中，iterations数量等于训练样本数除以batch_size。
• 在实践中，我们不能仅追求模型训练误差的最小，还需要结合模型验证误差以及泛化性能来评估模型能力。