前言

虽然我并不研究图神经网络，但是我认为图高效的表示方式还是值得所有人去学一下的，或许将来觉得这个很有意思呢？

当然啦，这也作为北京大学 图神经网络这门课的课程笔记吧，希望各位批评指教，也希望大家一起进步。

1.1图的定义

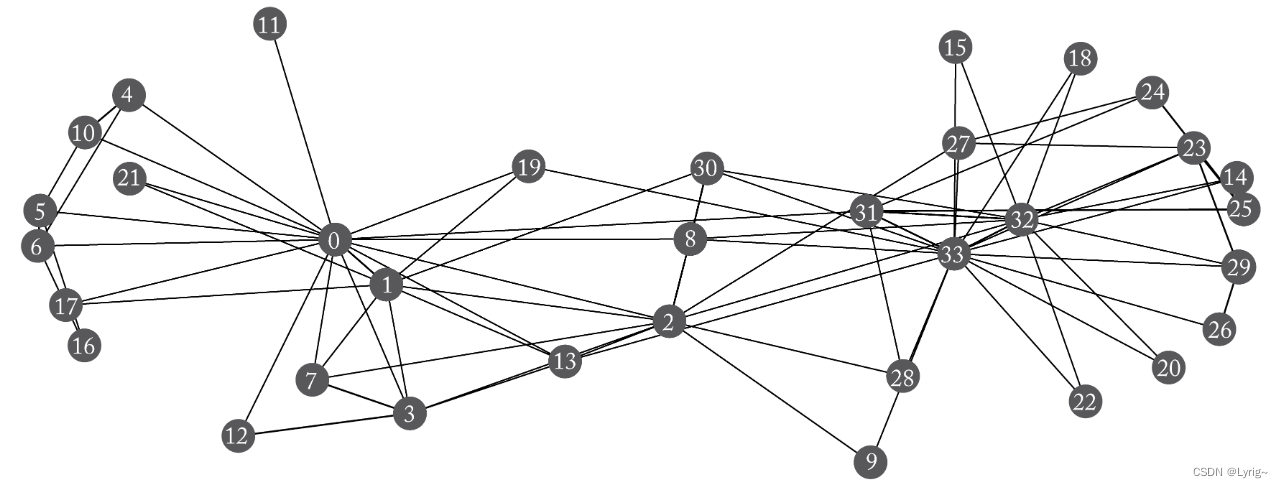
图可以定义为如下结构$$\mathcal{G}=(\mathcal{V},\mathcal{E})$$
包含节点集$v\in \mathcal{V}$和边集$(u,v)\in \mathcal{E},u,v\in \mathcal{V}$

对于边的表示，可以用邻接矩阵表示$A\in R^{|\mathcal{V}|\times |\mathcal{V}|}$，如果包含$(u,v)\in \mathcal{E}$，则$A[u,v]=1$。由此可得无向图的邻接矩阵为对称矩阵，而有向图则不一定。同时，如果我们给边带上权重，则$A[u,v]=r\in R$。

1.1.1多关系图

简单来说就是我们可以规定有多种边，这时，边表示为$(u,\tau ,v)\in \mathcal{E}$，其中$\tau$为我们规定的边的类型。这时对于每一个类型，我们都可以构建一个邻接矩阵$A_{\tau }$。把所有邻接矩阵合并为一个邻接矩阵向量，可以表示为$\mathcal{A}\in {\mathbf{R}}^{|\mathcal{V}|\times |\mathcal{R}|\times |\mathcal{V}|}$，其中$\mathcal{R}$为类型的集合。

下面介绍两类多关系图
异质图在这一类图中，节点也被分类，于是点集可以划分为完全不相交的集合的并集。$$\mathcal{V}={\mathcal{V}}_1\cup {\mathcal{V}}_2\cup ...\cup {\mathcal{V}}_k,{\mathcal{V}}_i\cap {\mathcal{V}}_j=\varnothing ,\forall i\ne j$$
图中的边通常根据节点的类型满足某些限制，如只连接同一类点之类的。

多路图我们假设一个图分为k层，节点在每一层都有相同的，这时我们认为每一层表达某个特殊的种类，于是我们可以有层内的边，也可以有层间的边。

1.1.2特征信息

为表达节点级别的信息，我们可以用这样$\mathcal{X}\in {\mathcal{R}}^{|\mathcal{V}|\times m}$。

1.2机器学习在图中的应用

1.2.1 节点分类

任务描述为，根据一幅图，给每个节点一个标签$y_u$，其中训练数据是我们会给定训练集中点的标签${\mathcal{V}}_{train}\subset \mathcal{V}$，这训练集可能是整个图中的一个小的子集，也有可能是大部分节点（让我们泛化不连接的节点）。

这任务不能简单理解为监督学习，最重要的不同是，图中的每个节点并非独立同分布的。对于传统的监督学习，我们通常要求采样的每个数据点都是独立的，否则我们需要对数据点之间的联系进行建模。同时我们也会要求这些采样的数据点是同分布的，否则我们无法保证模型的泛化性。而节点分类问题并不满足该假设，因为我们是在对互相联系的点进行建模。

例如，我们可以考虑节点间的同质性（如相邻的节点很有可能是一类的）、节点局部的结构等价性等。

1.2.2 关系预测

也成为连接预测、关系图补全等。

任务描述为对于一个图，我们给定一部分边集，作为训练集${\mathcal{V}}_{train}$，我们的目的是补全这个图的边。该任务的复杂度高度依赖于我们所验证的图的数据类型。

这一问题实际上模糊了监督学习和非监督学习，因为他需要从已有的知识中获得增益。

1.2.3 聚类和组织检测

如果说前两个任务更像监督学习，该任务则是无监督学习。

1.2.4 图分类、回归、聚类