题解43-48

124. 二叉树中的最大路径和 - 力扣（LeetCode）

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

思路:

树形dp,实际上是在树上做dp,通过任何一个节点的路径最大值等于左边节点的最大值加上右边节点的最大值加上当前节点的值,我们dfs函数返回的是当前节点的最大值,需要返回给父节点,需要和0取较大值,其他的就简单了

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = INT_MIN;
    int dfs(TreeNode* node)
    {
        if(node == nullptr) return 0;
        int left_ = dfs(node->left);
        int right_ = dfs(node->right);
        ans = max(ans, left_ + right_ + node->val);
        return max(0, max(left_, right_) + node->val);
    }
    int maxPathSum(TreeNode* root) {
       dfs(root);
       return ans;
    }
};

128. 最长连续序列 - 力扣（LeetCode）

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

提示：

0 <= nums.length <= 105
-109 <= nums[i] <= 109

思路:

哈希表来判断是否出现,我们只特判第一个数,故时间复杂度为 $O (n)$

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> st(nums.begin(), nums.end());
        int res = 0;
        for(auto&num : st)
        {
            if(st.find(num - 1) == st.end())
            {
                int last = num;
                while(st.find(last) != st.end())
                    last += 1;
                res = max(res, last - num);
            }
        }
        return res;
    }
};

136. 只出现一次的数字 - 力扣（LeetCode）

给你一个非空整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

输入：nums = [2,2,1]
输出：1

示例 2 ：

输入：nums = [4,1,2,1,2]
输出：4

示例 3 ：

输入：nums = [1]
输出：1

提示：

1 <= nums.length <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
除了某个元素只出现一次以外，其余每个元素均出现两次。

思路:

位运算,如果一个数出现了两次异或为0,所以异或完所有的数剩下的就是出现次数为1的数了

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        for(int i = 1; i < nums.size(); i ++)
            nums[0] ^= nums[i];
        return nums[0];
    }
};

139. 单词拆分 - 力扣（LeetCode）

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。

**注意：**不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
     注意，你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

提示：

1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅由小写英文字母组成
wordDict 中的所有字符串 互不相同

思路:

字符串哈希+递推

class Solution {
public:
    typedef unsigned long long ULL;
    const int P = 133;
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<ULL> hash;
        for(auto& word: wordDict)
        {
            ULL h = 0;
            for(auto& c : word)
            {
                h = h * P + c;
            }
            hash.insert(h);
        }
        int n = s.size();
        vector<bool> f(n + 1);
        f[0] = true;
        s = ' ' + s;
        // 前面一段是f[i]，最后一段是i+1..j
        for (int i = 0; i < n; i ++ ) {
            if (f[i]) { // 如果从1..i是有划分方法的，再去看f[i]为真会导致哪些f[j]为真
                ULL h = 0;
                for (int j = i + 1; j <= n; j ++ ) {
                    h = h * P + s[j];
                    if (hash.count(h))
                        f[j] = true;
                }
            }
        }

        return f[n];
    }
};

141. 环形链表 - 力扣（LeetCode）

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例 1：

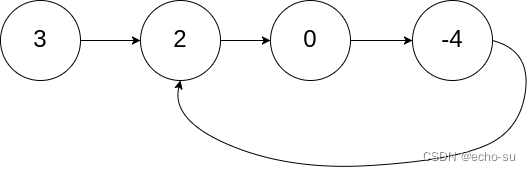
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

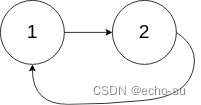
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。

**进阶：**你能用 O(1)（即，常量）内存解决此问题吗？

思路:

龟兔赛跑的故事,一个走两步,一个走一步,能够追上当且仅当出现了环

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *slow = head, *fast = head; // 乌龟和兔子同时从起点出发
        while (fast && fast->next) {
            slow = slow->next; // 乌龟走一步
            fast = fast->next->next; // 兔子走两步
            if (fast == slow) // 兔子追上乌龟（套圈），说明有环
                return true;
        }
        return false; // 访问到了链表末尾，无环
    }
};