本文为 「茶桁的 AI 秘籍 - BI 篇 第 14 篇」
文章目录
- 矩阵分解 ALS
- 常用推荐算法
- 什么是矩阵分解
- 矩阵分解的目标函数
Hi,你好。我是茶桁。
新年过后,咱们要开始学一些新内容了。从今天开始,要给大家去讲解的是关于推荐系统的内容。推荐系统的一些核心的原理会在今天开始的几节课中去给大家介绍,这个方法就是 ALS 方法。
ALS 方法的背景是来自于一场比赛,比赛的赛题是去提升 Netflix,一个电影网站的推荐率,如果你的推荐率能提升 10%,那么就会奖励你 100 万美金,是一个百万美金悬赏的一个比赛。
矩阵分解 ALS
ALS 方法提出的作者是个中国人,在完成这个比赛的时候还没有达到 10%,但是他发现这个方法确实可以提升。相比于 Netflix 官方的推荐系统的转化率可以提升将近 6% 的一个转化率,所以他也发表了一篇论文,这就是我们今天看到的一个内容。
这个场景也利用到现在的推荐系统里面一个很核心的一个方法叫做矩阵分解,这就是我要给大家去讲解的内容。我们看一看这些工具是如何来进行使用的,尤其在推荐系统里面都有哪些工具箱,未来你要做推荐的时候也可以使用它们,这是咱们之后几节课的主要内容。
首先,推荐系统 ALS 矩阵分解先去从整体上去了解。
- 推荐系统的算法都有哪些
- 什么叫做矩阵分解
- 矩阵分解里的 ALS 的方法指的是什么
ALS 方法其实是优化问题的解法之一,它只是其中的一种解法。可能更多人应该会了解一个方法叫做 SGD,SGD 在机器学习里面也是一个非常常见的优化的方式,帮我们调参数的。SGD 叫做随机梯度下降,梯度下降应该是机器学习非常核心的一个原理,它帮我们寻找参数的求解,每一次是沿着梯度的方向来进行优化,所以随机梯度下降是你的方向,是随机来进行选取的。所以 SGD 是贯穿了机器学习很重要的一个参数优化的一个过程。那 ALS 其实跟 SGD 是一样都属于优化方法,咱们就来看一看 ALS 是怎么样帮你去学习机器学习中那些参数的。
我们今天会给大家介绍 surprise,它是在 Python 里面的一个工具箱,它同时也是 scikit 家族。scikit 就是我们今天比较常见的一个叫做 sklearn 工具箱,它是 scikit 家族。所以推荐系统叫 scikit surprise,使用起来跟 sklearn 也很相像。
除了这个工具箱 Python 里面还有很多其他的工具箱,比如说像 lightFM,那在 scikit surprise 里面有一些推荐系统的算法,包括 baseline 的算法,SlopeOne 算法等等。
在这些学习同时,我会给大家带一个例子,一个非常经典的电影推荐系统。大概有十多万个电影和人们对它的一些评分,我们就想要去预测一下你还会对哪些电影感兴趣。利用已有的你对电影的评分的信息预测那些你没有看过的电影。这个就是一个电影推荐系统的一个场景。
那其中我们还要了解一些经典的 Python 中比较重要的一些使用的工具,这种工具基本上我估计大家应该都用过,你说不知道是不可能的。但是用的好不好其实差别还是挺大的,因为在实际的工作中调包可能就是一两句话的事情,但是前面的工作处理这些代码都是要自己写的,大部分的时间反而会是跟 DataFrame 来打交道。比如说怎么去选取这些特征列,这些特征列你需要做一些转换,构造一些新的特征,提取一些信息等等,这些都要去看。所以我们还会一起看一看 Python 的一些工具的一些常见的使用,以及今天会给大家进行讲解这个内容中对应的论文。我们一起读一读 ALS 的 paper。
估计很多小伙伴在学推荐系统之前没有太多的经验,可能以前也没有用过它,所以学习更像是一个反复的过程。第一次先从整体上去做了解,不用特别纠结于细节,细节的部分如果没有完全理解你可以先静下来。就有点像我们英语阅读的感觉是一样,先从整体上去了解。然后再去做第二次,去查看的时候可以重点去看一看之前不太了解那些细节。这些细节之间其实如果你仔细看的话,它跟我们以前的一些内容还是有关联的,比如说 SGD 随机下降。所以学习本身的过程是一个逐渐收敛的过程,你可能不是一次就能学到 100%。第一次有可能达到个六、七十分,第二次、第三次会越来越好。
首先咱们去看一下矩阵分解推荐系统,就是猜你喜欢。猜你喜欢背后怎么猜呢?是通过一个矩阵来做了一个分解,这个分解的方法是 ALS,我们推荐系统先从整体上给大家先看一看。
常用推荐算法
常见的推荐系统的方法分成两大领域,包括基于内容的推荐,还有基于协同过滤。这两种方法之间的区别是什么?基于内容的场景是你点了一篇文章,这篇文章属于什么属性我会基于它的属性来做推荐叫内容推荐。它跟协同过滤之间的区别主要看的是数据的来源。我们在之前的课程中也有给大家提到一些,推荐系统的算法是从这两个维度开始入手,一个是内容推荐,一个是协同过滤推荐。
协同过滤和内容推荐之间区别,内容推荐算静态的属性,协同过滤应该算动态的属性,所以协同过滤是人们的一些行为。那么动态属性里面现在大家研究的比较多的,使用的场景也很多。它又会分成两种,一个叫基于邻域的推荐,还有基于模型。邻域就是邻居,找你的邻居是谁。我们在之前的课程中讲过 UserCF 和 ItemCF 的区别,这两个就是先找用户的邻居叫 UserCF。找到跟你臭味相同的人,看一看这些人平时看什么样的电影,把他们看过的这些电影推荐给你,这叫 UserCF。ItemCF 是用户的以往的打分,这些打分,这个电影打分跟哪些其他的用户的打分更接近?叫 ItemCF,所以它也是一个邻居的概念。
那么基于模型,看到模型会想到什么?我们在写算法的时候这个 model 一般定义成为机器学习的模型。所以基于模型就是我们要去建一个 model,给了训练的数据去建模,建好模以后就可以拿它预测,这个就是基于模型的概念。在模型过程中会有基于贝叶斯,SVM 等等这一类型的概念,其实都是你建模的一些方法。SVM、贝叶斯,这些都是属于机器学习的一些方法,用它们的原理来进行学习和拟合。隐语义的模型里面又会分成矩阵分解、LDA 等等。最后给大家一张树图,可以更直观的看到它们之间的关系:

所以今天我们要学习的内容「矩阵分解」所在的位置是在协同过滤下,这个应该是用户的行为,没有行为的话就不会存在矩阵分解,我们都是对行为做的建模,所以又会处于基于模型机器学习的过程,隐语义模型里面又分,矩阵分解是在它下面的一个位置。顺便多说两句,矩阵分解简称为 MF,在隐语义模型里,还包括 LDA,LSA,pLSA 等方法。
那什么叫隐语义呢?隐语义,「隐」代表隐藏、隐含的含义。我们想要用用户和商品之间的关系,推荐系统就是给用户推荐商品,推荐 item。
那么 user 和 item 之间,我们认为它会存在一些隐藏的、隐含的一些联系。这样的 latent factor(隐含特征)连接着用户和商品之间。
user 是个用户,item 这是个商品。那如果中间存在一个隐藏的关系,这个关系一般可以把它称之为什么?我们这里就叫做 laten factor,也就是隐含特征,也可以把它称为叫做隐分类,但这些都比较学术。
用户有一些兴趣标签,商品也会有一些兴趣的分类,所以可以把这个隐的概念当成一个 interest,就是把用户按照一定兴趣划分,把 item 来做兴趣划分,所以它中间是可以连接起来,作为一个兴趣的属性连接彼此。而这个兴趣或者说它是个隐藏的、隐含的、隐晦的兴趣,实际上不是我们事先定义好的那些维度,而是基于行为自动的完成一个聚类的任务。
那我们学习机器学习这么久了,基础课也都学完的同学应该知道什么叫聚类。聚类它跟分类之间的区别有怎样的差别呢?在这个过程中之所以叫做隐,是因为我们采用的类似于聚类的一种手段。那么聚类它跟分类之间的区别大家在机器学习过程中如果有一些了解的话应该能知道,就是无监督。所以我们事先不知道它要分成哪些类别,只知道它自己无监督的方法,这就是聚类。因此我们把它称为叫做隐的概念。
那么聚的类别的个数,这个 k 值,就是人工可以去定义的参数。如果我们的粒度很粗,k 这个值就小一点,其隐特征少,这样的话我们划分的维度就会很粗。如果划分维度很细这个隐特征 k 应该就会大一点。
所以这个 k 是可以调节精细的程度的,如果想要让他预测的更加的准确一点可以让 k 变得大一些,大一点会更准确,但同时计算量也会更大。那么隐语义的概念,它的可解释性并不是特别好。这个「隐」是计算机能理解,但对于人来说聚类你就不太好清楚它聚成的这个物理含义是什么。相比之下我们会认为 ItemCF 可解释性会更强。因为 ItemCF 更像是相似度的一个推荐。这个 item 的向量和另一个 item 的向量谁会更接近,谁就会是更适合的商品。那 Latent 是按照我们的兴趣自动来进行划分,所以它的理解对计算机来说还能知道,人就不太好去理解。
还有就是在协同过滤过程中,刚才看到我们有两大分支,有模型的 model,还有邻域的。邻域是包括了 UserCF 和 ItemCF,有的时候我们也会把基于邻域这种概念叫做基于内存。如果你用的是 UserCF 或者 ItemCF,你会发现电脑内存会直接飙满标红。所以它是基于内存的协同过滤,这也是人们的一种称呼,因为它会非常的吃内存。
为什么非常吃内存?在计算相似度找邻居的时候,你是把所有的矩阵放到内存里面一起完成计算,这是个相对全量的数据。所以对你的内存要求会比较高。
如果你电脑是 16G 的或 32G,或者更高,那你们也可以试一试,基本上也能体验出来它是很吃内存的,这是基于邻域的概念。
基于模型的推荐(Model-based), 刚才提到是机器学习的方法,那么机器学习就需要分成两阶段:训练和测试。咱们应该能体会到,训练过程有可能往往会很长,但是一旦训练完成,机器学习基于模型的这种推荐的推理速度非常快。所以训练虽然时间长,但是使用起来效率还是非常高的。所以一般我会把它分成离线的训练和在线的推理这两个环节。
那讲到这里,我们都是在讲一些常见概念,大家可以先去理解一下,先看一看,稍后咱们会重点去看模型的使用。
什么是矩阵分解
在场景过程中我们的推荐系统为什么要用矩阵分解呢?这些系统实际上有两大场景,第一个叫评分预测。我们画一个大矩阵,这个矩阵分成 user 的维度和 item 的维度。user 是由 U1、U2…,一直到可能 U100。item 是 I1、I2…,一直到 I100。
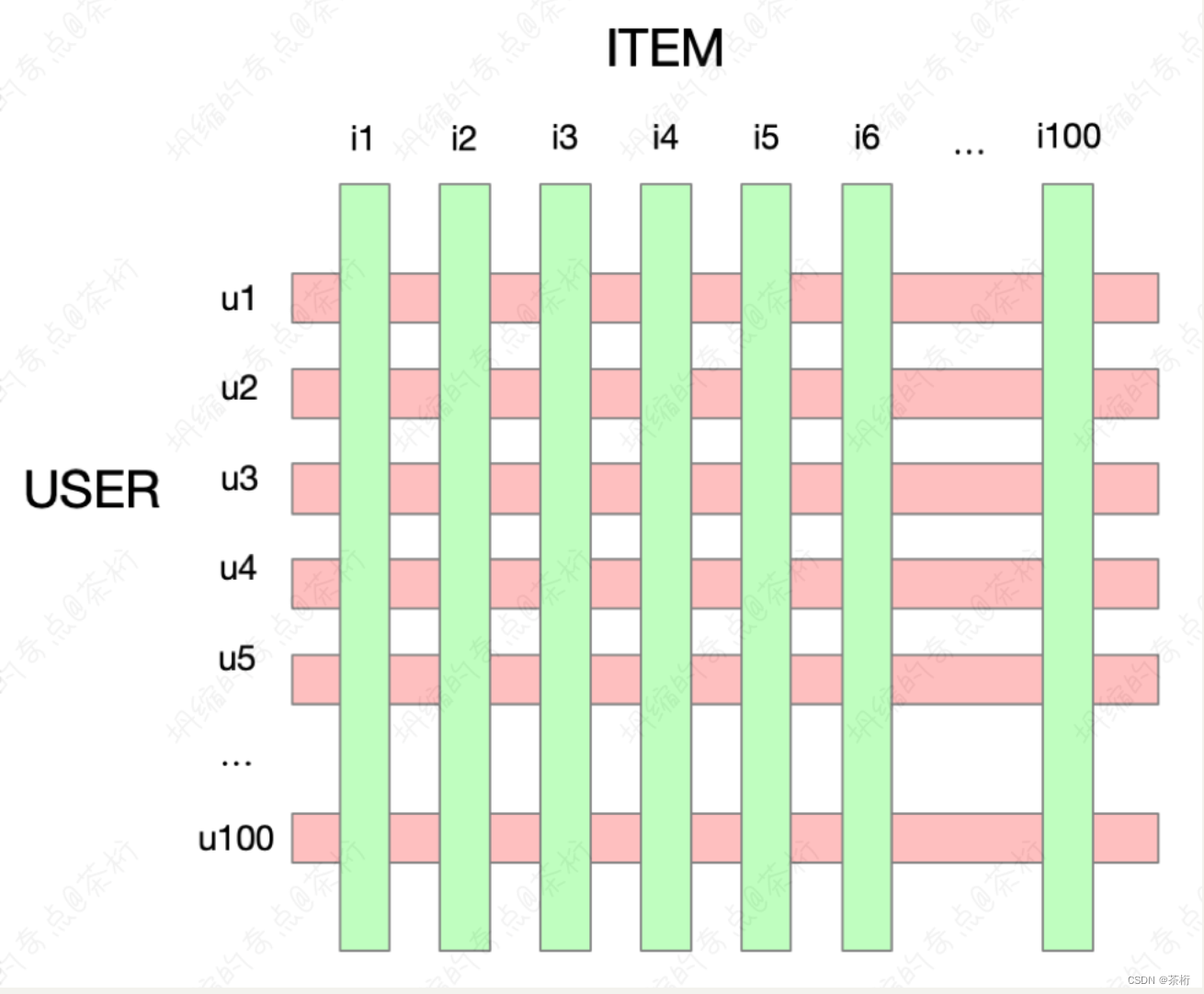
现在用户和商品之间会有个评分的矩阵,可能有一些分数,还有一些分数是没有的。那么我们要做的事情就是预估他没有去打分的,猜用户会打成多少分。这种类型叫评分预测问题,这种问题也就是我们要去讲解的矩阵分解,矩阵分解的任务就是预测一下用户和商品之间,之前没有打分到底会打多少分。
第二种类型叫 Top-N 推荐,Top-N 推荐就是不需要实际的分数,只要按照顺序给你提供一个感兴趣的列表就可以了。那你觉得这两个场景哪一個场景在推荐系统里使用的场景更多,更加高频?是第一个评分预测猜一个用户的打分,还是给用户推荐前 20 个商品,TOP 推荐?从业务场景上看的话,从我们自身需求看,不需要实际的具体的打分,只要把推荐类型给到就可以了,所以这个场景会比较多。
那为什么我们还会讲第一个呢?因为第一个和第二个之间也是有关系的。如果我们已经知道了第一个实际的评分,也能做第二个任务,就把后面那些未知的分数按照从大到小作排序给用户直接推荐就可以了。
所以这两个就是推荐系统里的两大场景,一个就到分数的粒度,一个就到推荐列表排序就可以。
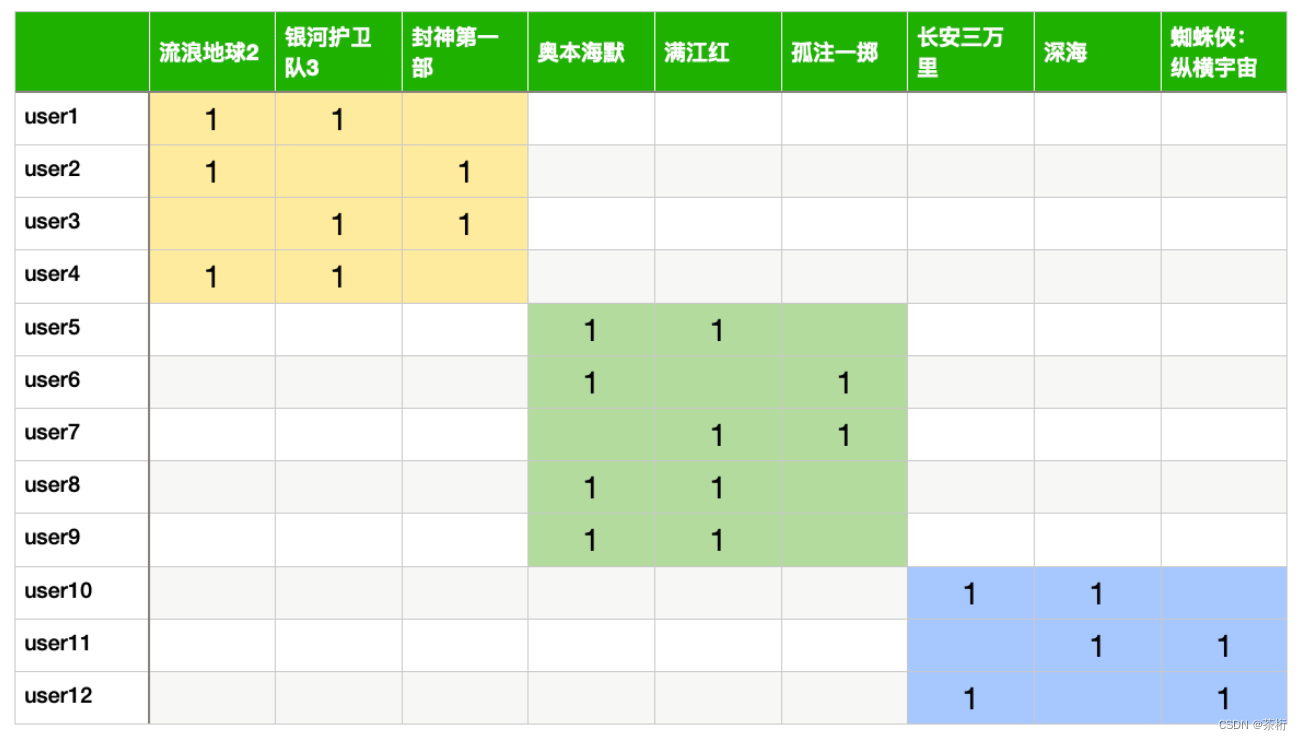
我们看一下推荐矩阵分解猜你喜欢。刚才提到这是猜用户对他的喜欢的程度打分的情况。这里举了个例子是 12 个用户 9 部电影,不是每个用户 9 个电影都看过都有反馈。这里标记的 1 代表喜欢,你也可以把它认为是打一个很高的分数。空白的地方,你看有些地方虽然标了颜色,但是是空白,代表用户没有反馈。还没有反馈不代表他不喜欢,所以这 12 个用户对 9 部电影我们现在只能收集到一部分数据。还有很多数据是没有收集到的。
大家觉得这个矩阵在实际的网站过程中拿到这个评分矩阵是稠密的还是稀疏的?稠密和稀疏是矩阵的一个特征,这个特征就对后续的算法就起到了一个很关键的一个决定作用,那这应该是是很稀疏的。
因为一个人不可能把所有的电影都看完,豆瓣上有 10 万部电影,你最多看个 1,000 部就已经很不错了,所以 99%的数据是空缺的。在 Netflix 这个网站里面,它告诉我们用户评分只有 1%的数据,就说大部分 99%格子是没有评分的。其实 1%这个数量已经很高了,所以它是一个非常稀疏的矩阵。
我们看到这个矩阵的问题,想把这个矩阵填上怎么填?矩阵分解的思路就是把一个大矩阵拆成两个小矩阵,分别拆出来,这是它的一个整体的概念。

原来又大又稀疏,这个长和宽称为 m 和 n,数值会很大,比如 100 万的用户,10 万的电影,绝大部分都为空值。那拆成小矩阵,user 里面我们会设定一个 k。user 就是用户要用兴趣来做表达,这个 k 值一般应该会很小。通常情况下这个 k 是远远小于 m 和 n。比如说它可能只有 100,那只有 100 相比之前的 100 万和 10 万来说就会非常非常的小。item 也是一样,可能 k 值也是固定的,也是 100。这样就把一个大矩阵拆成了两个小矩阵。拆完以后我们最后得出来的会不会能把这个矩阵还原出来?一会我们可以实际的看一看。
那怎么拆呢?我们以今天这个例子为例,现在数据量级比较小,只有 12 个用户和 9 个电影。行数是 12,现在 User 矩阵的行数也是 12,我们把 k 取成了 3,k=3 的概念相当于是把用户分成了三种类型。
哪三种类型,我们可以看上面一个具体的图表标识。用户我们假设它会分成三种类型,电影这里的 k 也分成三种类型。
先以电影为例,流浪地球 2、银河护卫队 3 和封神第一部这类型的电影应该是属于特效片对吧?我个人是这样划分的,那奥本海默、满江红和孤注一掷属于剧情片,后面三个就是动画片了。
把电影这 9 部电影分成三种类型,第一种类型它们三个是聚成一起去,它们在某些维度上可能会更加接近。流浪地球 2 银河护卫队 3、封神第一部属于特效片。奥本海默、满江红和孤注一掷这三个聚到一起去,属于剧情片。
所以隐分类的概念就是能给它聚成一起,但是没有一个明确的定义。最后三部聚成一起,你可以把它叫做卡通片,也可以叫儿童片,也可以叫动画片都是可以的。那这样我们就会把它记录成三种类型。
比如说我们认为说一部电影可以有三种类型,特效片、剧情片和动画片。那一个人也是相同的三种类型。
一个人会有三种类型,一个片子也有三种类型。那一个电影有没有可能会横跨两个类型呢?就是在这两种类型上都有取值,而且这个取值都不低。或说一个人有没有可能在两种类型上都有取值,还是说我们只能把它划分成一种?
举个例子,一个片子有没有可能横跨两种?这个片子既属于特效片,也属于剧情片,有这种可能性。所以这种类别它不是一个唯一的属性,它只是聚成几类。我们把这个类别去做一个特征的描述,在上面会有个分值,这个分值代表特征的显著性。用户也会在这三种类型上面有它的分值,代表它的显著性。
那我们就把它拆出来,原来这个象限很多,12*9,现在这个象限大家可以一起来数一数,User 的矩阵行数应该是 12,列的话变成 k 等于 3。
item 矩阵,它的维度应该是行数变成了 3,行数这里是 k。列就是它的 item 的个数是 9。12*3, 3*9,这两个如果做乘法,把它乘完以后,请问它的矩阵维度会是多少?
矩阵相乘,那中间都有一个 3 是相等的,如果这里不相等是没有办法做乘法的。那这其实也就是 12 乘以 9。这样我们就会把它拆成了两个小矩阵,拆完以后再组装起来还会得到一个 12*9 的矩阵。
每一个用户上面 k 等于 3,每一个用户这三个值可不可能都是稠密的呢?原来(12,9)是稀疏的,现在变成了 User 矩阵,(12, 3),做了一个降维处理,这个降维的处理就是在很粗的或者在很细微的这种粒度上面,你拿放大镜去看,它可能不是每个片子都可以给你打分了,但是你在上面抽象,就像看我们的地图一样,它会变得很稠密,所以它就会更加密一点。
一般如果我们要进行聚类的话这个聚类很少聚的类别很多,一般可能 100 类就已经很大了。所以每个格基本都有值,很容易都有值,所以它就会变成稠密。如果 User 的矩阵是稠密的,item 矩阵是稠密的,这两个稠密的矩阵相乘,乘完以后还能得到原来的 12 乘以 9,请问得出来的这个新的 12*9 的矩阵它是变成了稠密还是也是稀疏的?
最后得出来的这个矩阵跟之前相比,原来是稀疏的,因为原来我们要拆评分,所以大部分为空。现在如果我们要把它降维处理了,变成了12*3和3*9,降维成两个稠密的矩阵,最后乘完以后应该也能是稠密的矩阵。所以这两个矩阵乘完以后我们就相当于是对原来矩阵做了一个补全的问题。
这个概念就是说为什么采用分解做,分解的概念就是用聚类的思想作降维,把原来稀疏的矩阵,又大又稀的 12 乘以 9 变成了12*3和3*9的这样的小矩阵,每个小矩阵都稠密了,然后再做乘法,还原出来的12*9的大小,它也是个稠密矩阵。
我们现在要求的这个问题是猜你喜欢,以这个例子为例,猜什么?猜用户对其打分是什么。有些可能高一点,可能一有些可能少一点,是 0。那我们要把它预估出来,这是我们的目标。
预估就是要把原来稀疏的变成稠密的,就把这个空给填上。怎么填呢?可以把一个大矩阵拆成两个小矩阵,每个小矩阵都很容易稠密。
因为你在很微观的粒度上面,看了 10 万部电影,不是每部电影都会打分。但是你在宏观上分成三类型,三种类型你肯定是要打分的。比如说这个用户对特效片喜欢我们就高一点,0.98,动画片不喜欢低一点,可能 0.01,剧情片可能中等,可能 0.57 等等。这样每一个分值就基于他以往的行为,我们可以给它打出来这个分数。
那数据的信息量在哪个步骤增加呢?数据的信息量是在做预测的方式增加,实际上有点类似于像一个图像,我们拍了一张照片,但这个照片像素有缺失,把它抠下了一块,把它拆出来再还原给它补上。所以数据的信息量是我们通过建模的方式预测出来那些原来空的数据的过程。那现在 Photoshop 以及 DELL-3,还有其他的一些填补或者扩展图像也都是基于这个原理,只是它们会基于更大的数据量来完成的模型,所以表现会更好。
回来我们之前的案例,比如说每个用户都可以从特效片、剧情片和动画片上去打个分数,分数高代表你的特征明显,这种类型的电影更容易打高分,分数如果低呢特征就不明显。

通过学习,如果我们已经学完了这个参数,user1 给这三个类型分别的打分是 0.93,-0.09,0.08,就证明用户对特效片是感兴趣的,剧情片是不太感兴趣的。

每个用户都打上了这种类型。每个片子也可以打上这三种类型,那这三种类型我们就可以做还原。预测值填补了原来的空缺的缺失值。
这两个矩阵,我们把 user 的矩阵和 item 矩阵都预测出来了,再做乘法,得出来的矩阵是 12*9,那这会儿12*3的这个矩阵是稠密的,3*9是稠密的,比较明显我们乘完以后一定也是稠密的。
第一个用户之前只是对流浪地球 2 和银河护卫队 3 有反馈,是喜欢的,其他的没有反馈。不代表他不喜欢,只能代表他没有反馈给我们,那我们要去猜。那对于第一个用户,如果你要给第一个用户推荐两部电影请问你会推荐哪两部电影呢?还能再推荐流浪地球 2 和银河护卫队 3 吗?他已经看过了,所以应该会猜之前没有看过的。
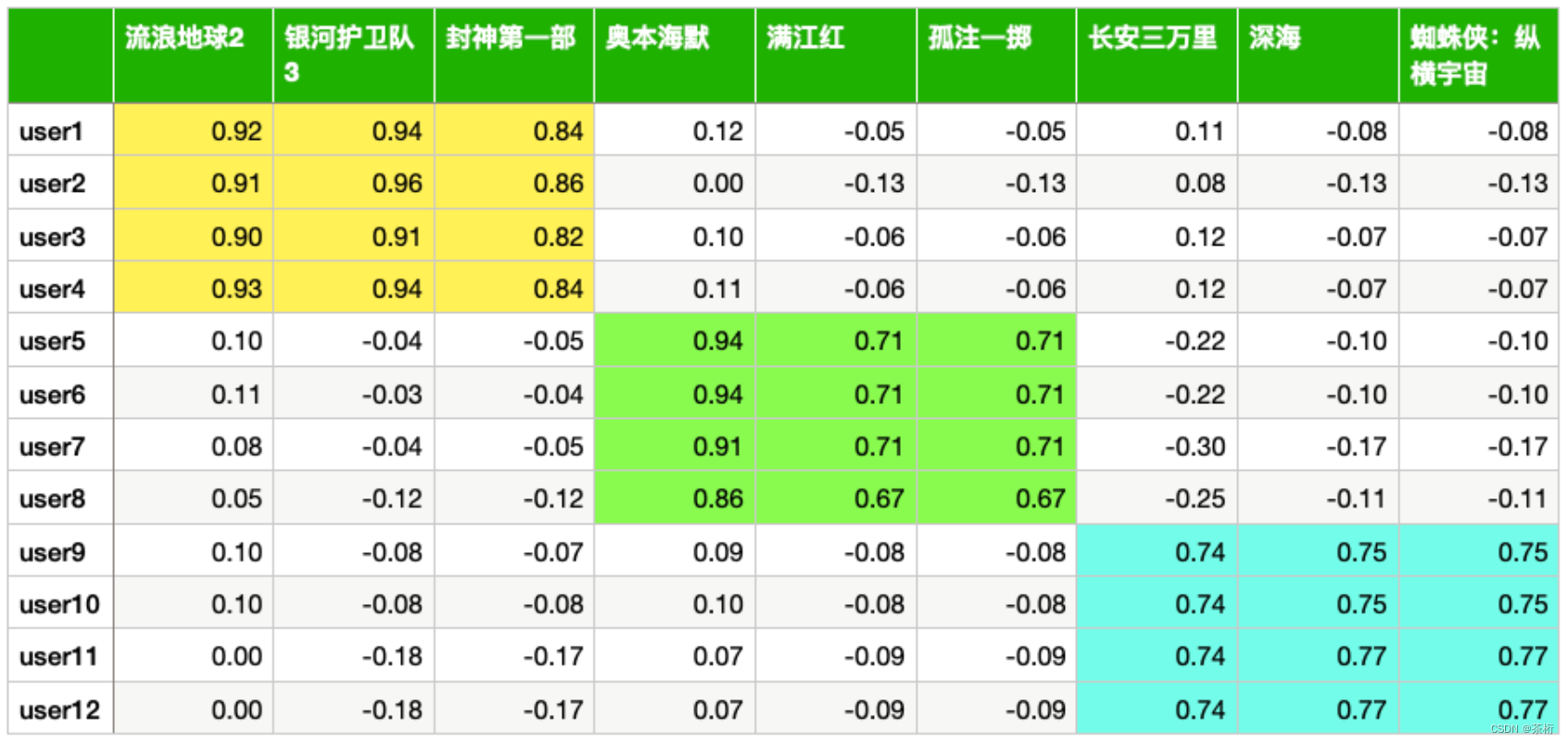
这样,我们已经预估出来了他对封神第一部感兴趣,分值要从大到小来做排序可能第一部应该是封神第一部,第二部就是奥本海默,给他做相关的一个推荐。
就是说我们通过预测补全的方法猜用户没有打分的电影会打多少分,然后从大到小来做相关的一个推荐,这是我们整个矩阵分解使用的一个逻辑。那这个使用逻辑为什么它能成立,背后的原理是什么?
矩阵分解的目标函数
它背后的原理实际上是一个建模的概念,回到我们之前的那个图形:
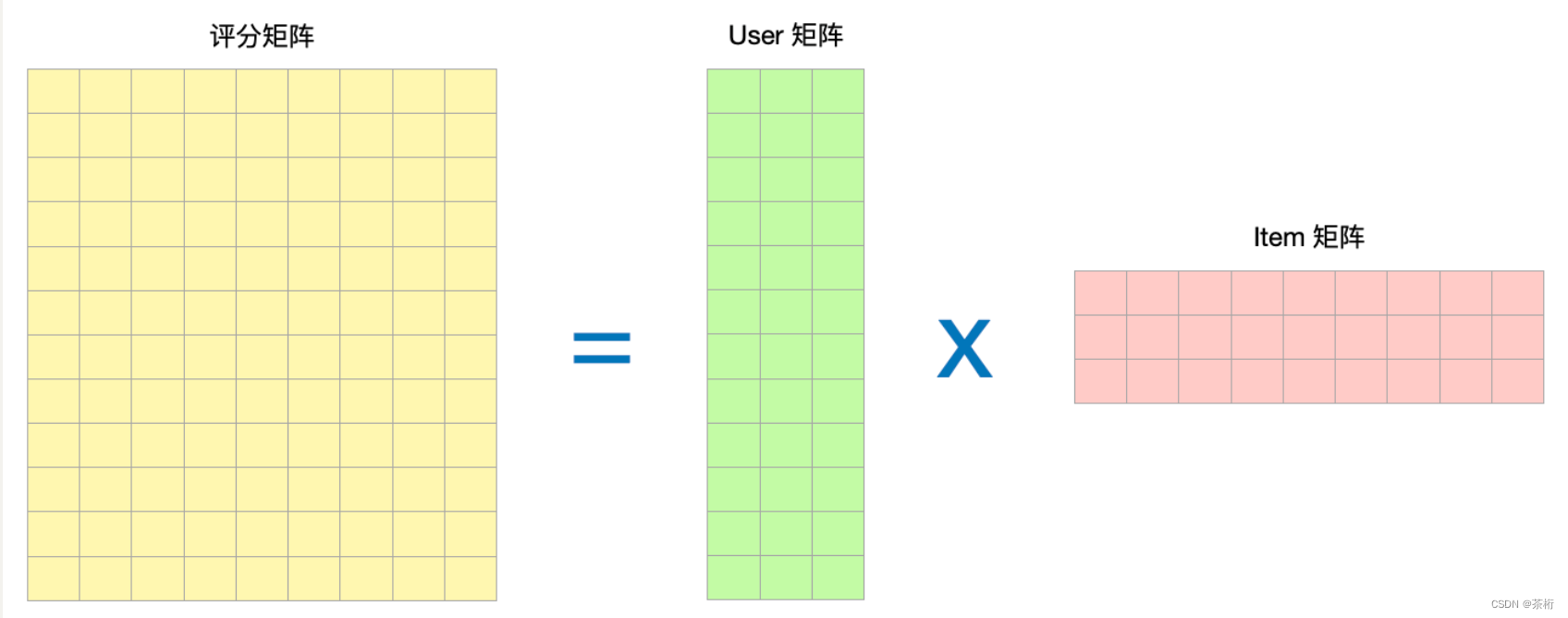
左侧的评分矩阵,我们将其称为 R 矩阵rating,这是已知矩阵。user 矩阵和 item 矩阵这两个矩阵现在是已知的吗?原始数据并没有,它是未知,是我们要去学的参数。所以我们想要通过已知的 Rating 自动地学出来两个矩阵,分别叫做 user 矩阵、item 矩阵。这两个矩阵学完以后,怎么评价它学的好坏呢?机器学习里面我们想要把学出来的结果和实际的结果做个对比,如果我们要做回归任务就要做一个 loss function。回归任务的话就是 0-5 分的电影打分,那回归任务的 loss function,也就是损失函数,它就是 MSE,如果是 MSE 的话相当于我们预测出来这个结果就是
∑
(
y
′
−
y
)
2
\sum(y'-y)^2
∑(y′−y)2,要让它最小,这就是我们的 MSE。
我们原来已经有值了,还有一些地方是之前没有告诉我们这个值,我们把已经有的值的差的平方算进去,没有的地方差的平方要不要也算进去呢?
也就是说,12*3和3*9,最后乘完以后会得到一个新的评分矩阵,我们称其为 R’, 这个 R’和原来的 R 之间,有些是重叠的。原来是已知的,现在预测出来结果还有一些是你原来未知的,那么在计算 MSE loss 方式的过程中要不要把未知的那些空,误差也算进去?
其实是不要算进去的,因为你其实并不知道它实际答案,比如说我们以前面的原始数据为例:

我们来看,user1 对封神第一部是没有评分的,如果你要计算的话能算 0 分吗?因为没有评价不代表不喜欢,实际上这个用户对封神第一部可能是喜欢的,所以你其实并不知道他实际的结果,因此我们无法去预估那些未知的实际值,在计算 MSE,去拟合过程中只能拿已知的值。
所以我们只需要拿已知的部分让它评分最小就可以了,这个就是一个优化问题。我们以前计算 MSE 的过程中,就是要去预测一个结果,希望你预测这个结果和实际的答案更加接近。那么怎么去预测呢?是通过参数来做预测,不论你用 SVM,用 LR 还是用什么,你学出来都是它的参数,参数固定了结果就会固定。所以你学完这些参数如何使得它预测出来的 y’和实际值最小化就是我们优化的问题的定义的一个方法。
有了这个定义方法我们怎么去学习?这里先用一些向量来作表达, r u i r_{ui} rui是评分矩阵里面用户对商品的评分,表示用户 u 对 item 的一个评分。当其大于 0 时,表示有评分,当它等于 0 时,表示没有评分。这里不代表不喜欢它,只是说没有评分。
x u x_u xu表示用户 u 的向量,k 为列向量, y i y_i yi表示 i t e m i item_i itemi的向量,k 为列向量。用户矩阵 X, 用户数为 N:
X = [ x 1 , x 2 , . . . , x N ] \begin{align*} X = [x_1, x_2, ..., x_N] \end{align*} X=[x1,x2,...,xN]
商品矩阵 Y,商品数为 M
Y = [ y 1 , y 2 , . . . , y N ] \begin{align*} Y = [y_1, y_2, ..., y_N] \end{align*} Y=[y1,y2,...,yN]
为什么是 k 为列向量?因为这里的 k 是已分类,想让它做一个近似的降维的处理。
那我们要去建这个模型,去建 loss function,机器学习的本质要去解这个问题主要是通过目标函数,就是规定了要学的一个方向,把这个方向定义下来,那我们的目标就是找到一个参数让它的目标函数最小化。
m i n X , Y ∑ r u i ≠ 0 ( r u i − x u T y i ) 2 + λ [ ∑ u ∣ ∣ x u ∣ ∣ 2 2 + ∑ i ∣ ∣ y i ∣ ∣ 2 2 ] \begin{align*} min_{X,Y} \sum_{r_{ui}\ne 0}(r_{ui}-x_u^Ty_i)^2 + \lambda\left[ \sum_u||x_u||_2^2 + \sum_i||y_i||^2_2 \right] \end{align*} minX,Yrui=0∑(rui−xuTyi)2+λ[u∑∣∣xu∣∣22+i∑∣∣yi∣∣22]
我们的定义这里用的是 MSE,因为要做评分预测,有可能是一个 0-5 的分值。rui 是实际评分,x,y 就是拆出来的两个维度,user 和 item,拆出来这两个矩阵让它相乘,它也能得到一个值。让这两个值的平方和最小化,前面专门写了一个判断条件:rui 不等于 0。为什么要写这个,rui 如果不等于 0,它能代表它是有值的部分,所以前面这个是我们实际评分的误差要最小化。
那在训练过程一般来说定义它就可以了,这是一个理想的状态。后面我们还把我们训练模型中的参数也放到了这个计算里面去。x 和 y 是我们要去学习出来的用户矩阵和商品矩阵,让它们的参数的平方和再加一个 lambda 作为第二项。
我们前面就已经要让它预测结果会更小化,那为什么有的时候我们还会加一个第二项呢?之前给大家讲过 XGBoost 和 LightGBM,如果大家学习过的话就发现,在工程上面一个很重要的过程就是要添加正则化项。它的目的就是解决我们泛化能力,防止过拟合。
所以前面是我们的目标,我们在目标里面又加了正则化项,让其更加泛化,这样就会让这个参数抖动起来不会这么的剧烈。
防止过拟合之前给大家讲过例子,之前是给大家说了一个场景,同样都是达到月薪 2 万块钱的目标,a 和 b 方式不一样,a 的参数抖动比较强,就像一个滴滴司机,每天早上可能 9 点就出门晚上 12 点才回来。这样他一个月也能赚 2 万块钱。b 是一个办公室的白领,朝九晚五,一个月也能赚 2 万块钱。那请问如果你要去做的话你是做 a 还是做 b?
都是达到了月薪 2 万,大部分肯定希望觉得 b 会更合理一点。因为 b 的参数抖动没有这么剧烈,对于 a 来说就抖动很强。这个参数在后面,第二项它整个的代价就会比较小,这衡量我们学习的代价。
有了机器学习去解这个目标,要用到一些优化的方法。下节课,咱们就来看看其中的一个方法,ALS。