差分与前缀和

求差分 与 求前缀和 是一组“互逆”的操作。

使用差分 可以实现：以时间复杂度为O(1)，对数组区间各元素 / 矩阵区域各元素 ± 一个常数。

使用前缀和 可以实现：以时间复杂度为O(1)，对数组区间各元素 / 矩阵区域各元素 进行快速地 求和。

为了便于理解，可以将差分与前缀和理解为 数列各项 与 数列的前n项和 。

• 前缀和：Sn = A1 + A2 + A3 + … + An；

• 差分(为了避免歧义，此处将下标用括号括出)：A(n) = S(n) - S(n-1)；

以下为差分与前缀和的具体内容：

1. 前缀和

前缀和是一种常用的算法技巧，通常用于快速求解 数组区间求和 和 矩阵区域求和 的问题。

1.1 前缀和数组

已知数组 a[n] ，遍历数组并计算 每个位置之前所有元素的和，将其存储到数组s[n]中，以便在之后的查询中可以快速得到区间和。【注：为了便于处理，前缀和的数组下标从 1 开始，且s[0] = a[0] = 0】

• 前缀和的定义

  • s[1] = a[1]
  • s[2] = a[1] + a[2]
  • s[3] = a[1] + a[2] +a[3]
  • s[n] = a[1] + a[2] + a[3] + … + a[n]

  根据递推关系，可以得出: s[i] = s[i - 1] + a[i]

• 若要求 a[l] + a[l + 1] + … + a[r] ，即数组下标范围为[l, r]的元素之和 (暂写作a[l, r])。则有：

  a[l, r] = s[r] - s[l - 1]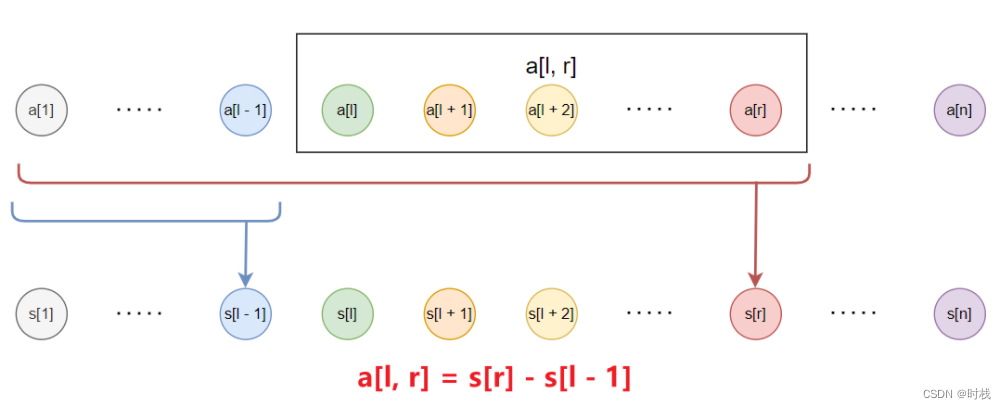

  

• 代码模板

  //初始化
  a[0] = 0;
  s[0] = 0;
  
  //数据输入
  //前缀和，数组的下标从1开始
  for(int i = 1; i <= n; i++){
      scanf("%d", &a[i])；
  }
  
  //计算前缀和
  for(int i = 1; i <= n; i++){
      s[i] = s[i - 1] + a[i];
  }
  
  //计算a[l] + a[l + 1] + ... + a[r]
  //（此处存在多个求和操作，仅写一个作为示例）
  ans = s[r] - s[l - 1];
  

1.2 前缀和矩阵

已知矩阵 a[n][m]，在遍历矩阵的过程中，将矩阵各个点与原点围成的矩形之中的所有元素的和预先计算出来，并存储到s[n][m]中，在之后的查询中可以快速得到区域和。

• 前缀和的定义

  s[i][j] = a[1][1] + a[1][2] + ... + a[1][j]
           +a[2][1] + a[2][2] + ... + a[2][j]
           + ...
           +a[i][1] + a[i][2] + ... + a[i][j]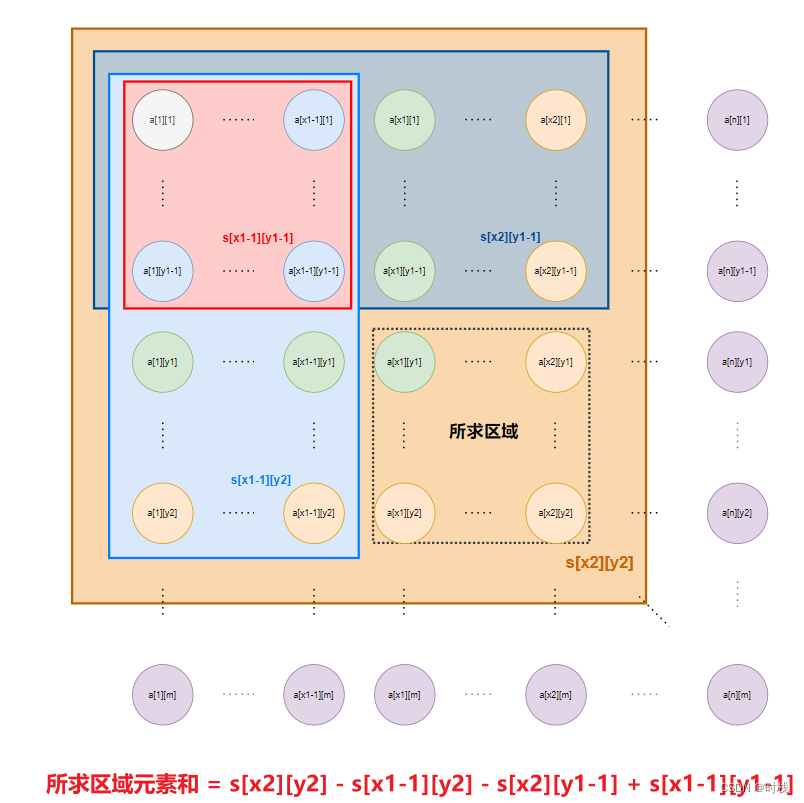
  

  

• 根据容斥原理，可以发现，橙色区域，如果扣除蓝色和青灰色区域的元素和的话，会把红色区域扣除两次，所以，橙色区域元素和在减去蓝色和青灰色区域的元素和之后，还需要加上红色区域，即所求区域【[x1,y1]和[x2,y2]确定的区域】的元素和为：

  ​ s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 -1][y1 - 1]

• 代码模板

  //初始化：
  //需要把 s[0][0] ... s[0][m] 与 s[0][0] ... s[n][0] 初始化为0
  
  //输入
  for(int i = 1; i <= n; i ++){
      for(int j = 1; j <= m; j ++){
          scanf("%d",&a[i][j]);
      }
  }
  
  //计算前缀和
  for(int i = 1; i <= n; i ++){
      for(int j = 1; j <= m; j ++){
          // s[i - 1][j] 和 s[i][j - 1] 均覆盖 s[i - 1][j - 1]区域
          // 即 s[i - 1][j - 1] 区域被计算了2次，需要减去1个 s[i - 1][j - 1]
          s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
      }
  }
  
  //（此处存在多个求和操作，仅写一个作为示例）
  ans = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 -1][y1 - 1];
  

• 备注：关于前缀和的计算

  

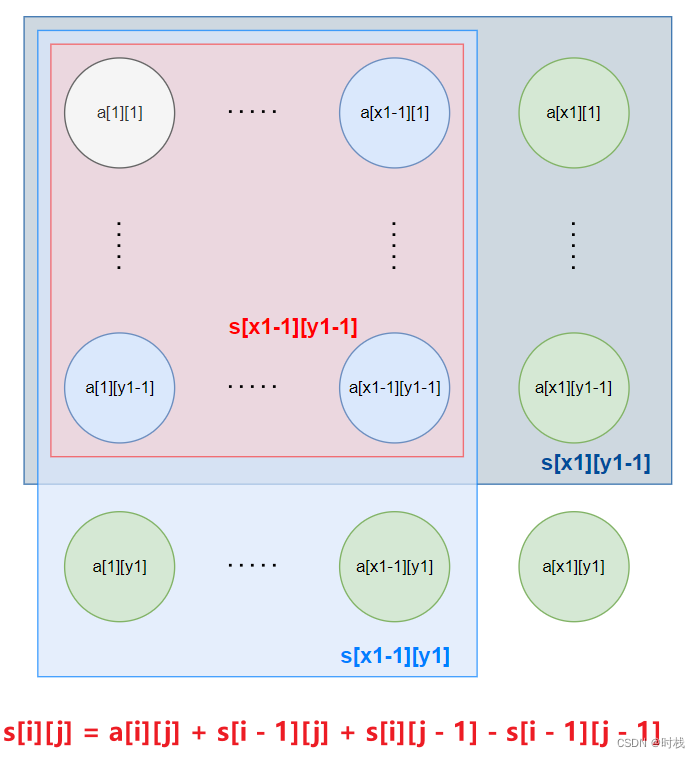
2. 差分

差分可看作前缀和的逆运算，常用于处理连续序列的增量变化。它可以在一维数组或二维矩阵中快速且高效地更新区间/区域的元素值。

2.1 差分数组

已知数组a[n]，当存在大量的数组区间操作（增/减常数值）时，可以先求出该数组的差分数组b[n]，然后再进行变更操作，最后通过差分数组还原出变更后的数组a[n]。

• 差分的定义

  b[1] = a[1]
  b[2] = a[2] - a[1]
  b[3] = a[3] - a[2]
  b[4] = a[4] - a[3]
  ...
  b[n] = a[n] - a[n - 1];
  

  如果对左右两边分别累加，可得：
  a[n] = b[1] + b[2] + b[3] + ... +b[n]
  

• 当需要给 a[l], a[l + 1], a[l + 2] ... a[r] 分别加上 常数c 的时候，仅需进行以下操作即可实现：

  • b[l] = b[l] + c

  • b[r + 1] = b[r + 1] - c

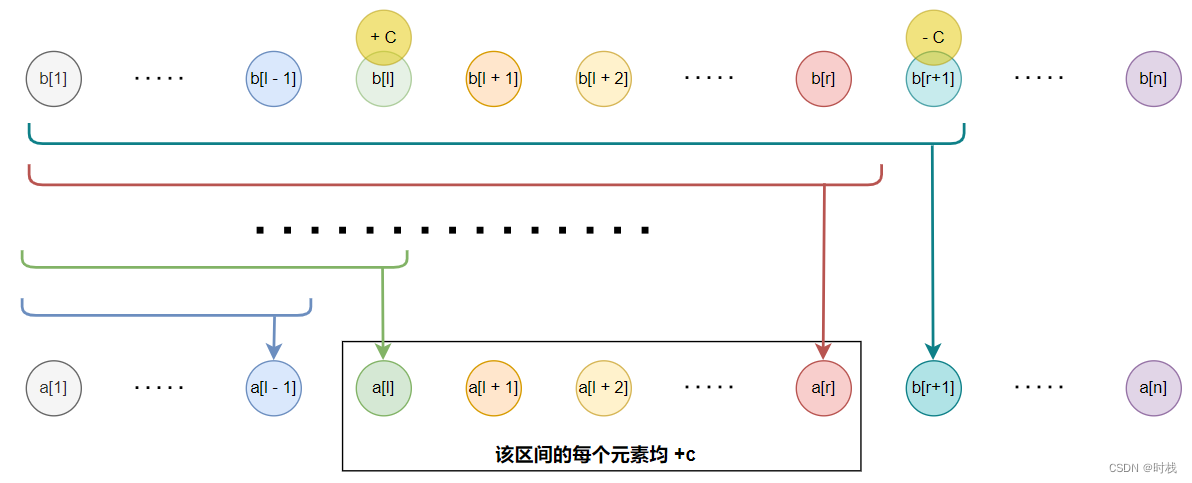
  • 如下图所示：

    • a[l]之前和a[r]之后（不包括a[l]和a[r]）的元素均不受影响
    • a[l]之前和a[r]之后（包括a[l]和a[r]）的元素均增加了c
    • 注意：此处仅对b[n]数组进行操作，需要累加求和才能得出变更后的数组a[n]。

    

• 代码模板

  //初始化时，将a[n]与b[n]中的所有元素均为0
  //此时，满足 b[n]是a[n]数组的差分数组 的条件（b[n]所有值均为0，累加后也均为0）
  
  //输入
  //下标从1开始
  for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
  
  //差分数组初始化
  //因为当前a[n]与b[n]中的所有元素均为0，满足b[n]是a[n]的差分数组
  //此时可以看作，在数组a[n]中，依次把区间[i,i]的数均加上常数a[i] （注：此处i的取值范围为[1, n]）
  //因此,在插入a[i]时，只需令
  //    b[i] = b[i] + a[i]; 
  //    b[i + 1] = b[i + 1] - a[i];
  for(int i = 1; i <= n; i++){
      b[i] += a[i];
      b[i+1] -= a[i];
  }
  
  //进行区间操作（此处存在多个区间操作，仅写一个作为示例）
  //给 a[l], a[l + 1], a[l + 2] ... a[r] 加 c
  scanf("%d%d%d", &l, &r, &c);
  b[l] += c;
  b[r + 1] -= c;
  
  
  //最后计算数组a[n]并输出
  for(int i = 1; i <= n; i++){
      a[i] = b[i] + a[i - 1];
      printf("%d ", a[i]);
  }
  

2.2 差分矩阵

类比于一维数组，在面对“给矩阵 a[n][m] 的子矩阵中每个元素加/减一个常数”的情况时，也可以构造矩阵 a[n][m] 的差分矩阵 b[n][m] （此时 a[n][m] 是 b[n][m] 的前缀和矩阵），来实现在O(1)时间复杂度的情况下进行子矩阵各元素的变更。

• 差分的定义

  • 对于a[n][m]的差分数组b[n][m]，（矩阵的下标均从1开始）有：
    
    a[i][j] = b[1][1] + b[1][2] + ... + b[1][j]
             +b[2][1] + b[2][2] + ... + b[2][j]
             + ...
             +b[i][1] + b[i][2] + ... + b[i][j]
    

  • 当需要给(x1,y1)与(x2,y2)确定的子矩阵（目标区域，如下图所示）中的每个元素 +c 时，需要进行以下操作：

    • b[x1][y1] = b[x1][y1] + c
    • b[x1][y2 + 1] = b[x1][y2 + 1] - c
    • b[x2 + 1][y1] = b[x2 + 1][y1] - c
    • b[x2 + 1][y2 + 1] = b[x2 + 1][y2 + 1] + c

  • 

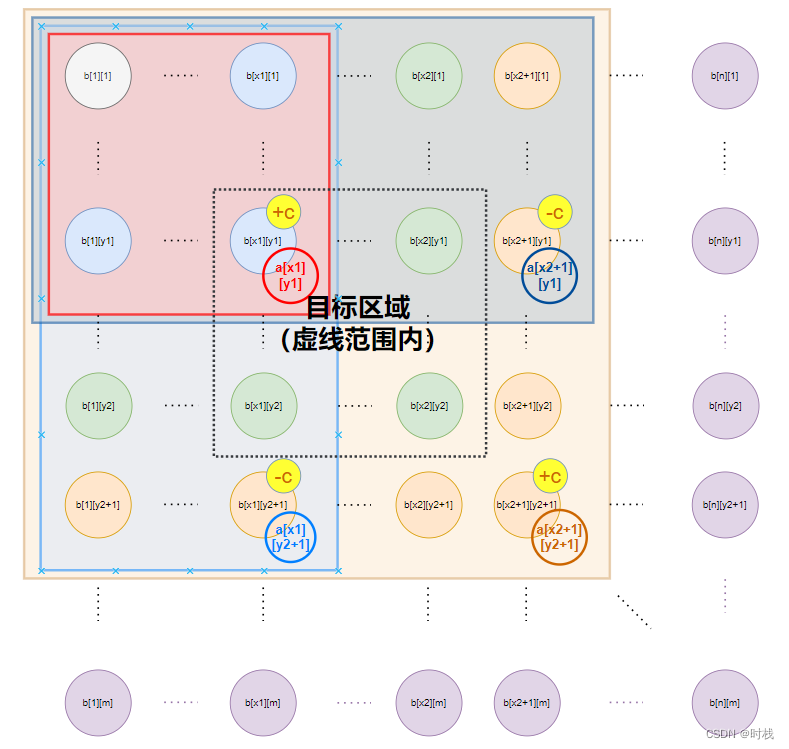
• 代码模板

  //初始化时，将a[n][m]与b[n][m]中的所有元素均赋值为0
  //此时，满足：
  //  a[n][m] 是 b[n][m] 的前缀和矩阵
  //  b[n][m] 是 a[n][m] 的差分矩阵
  
  //矩阵的输入
  //下标均从1开始
  for(int i = 1; i <= n; i++){
      for(int j = 1; j <= m; j++){
          scanf("%d", &a[i][j]);
      }
  }
  
  //差分矩阵初始化
  //因为 b[n][m] 是 a[n][m] 的差分矩阵（所有的值全部为0）
  //此时可以看作对点(i, j) 进行 +c 的操作（令x1 = x2, y1 = y2, 矩形区域就变成了一个点）
  //我们已知 (x1,y1)与(x2,y2)确定的子矩阵中的每个元素都 +c 的操作，所以可以：
  //令 x1 = x2 = i; y1 = y2 = j;  c = a[i][j]
  //按照这种方式，依次遍历所有元素就可以完成对差分矩阵的初始化，代码如下：
  for(int i = 1; i <= n; i++){
      for(int j = 1; j <= m; j++){
          b[i][j] += a[i][j];
          b[i][j + 1] -= a[i][j];
          b[i + 1][j] -= a[i][j];
          b[i + 1][j + 1] += a[i][j];
      }
  }
  
  
  //进行区域操作（此处存在多个区域操作，仅写一个作为示例）
  //给(x1,y1)与(x2,y2)确定的子矩阵（目标区域，如下图所示）中的每个元素 +c：
  scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
  b[x1][y1] += c;
  b[x1][y2 + 1] -= c;
  b[x2 + 1][y1] -= c;
  b[x2 + 1][y2 + 1] += c;
  
  
  //最后计算矩阵a[n][m]并输出。
  for(int i = 1; i <= n; i++){
      for(int j = 1; j <= m; j++){
          a[i][j] = b[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
          printf("%d ", a[i][j]);
      }
      printf("\n");
  }
  
  

• 备注：关于差分矩阵的初始化

• 

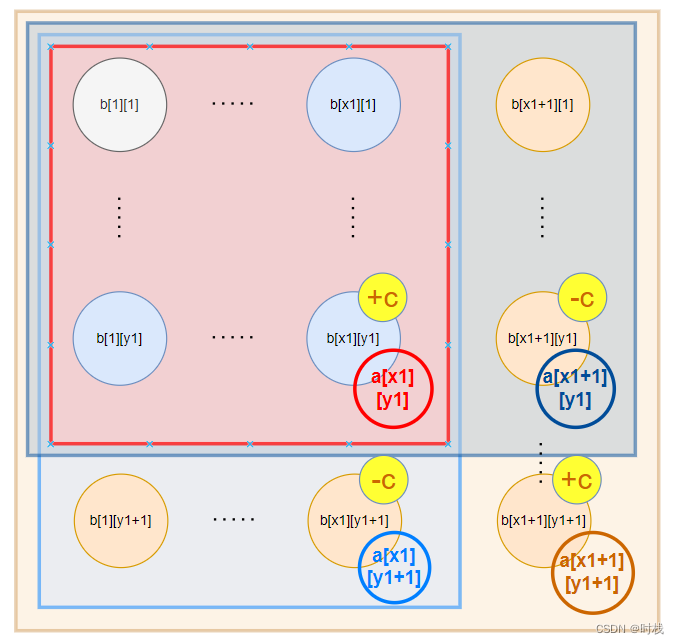
本文是学习AcWing算法基础课的总结，请见：
https://www.acwing.com/activity/content/11/

如有不当或错误之处，恳请您的指正，谢谢！！！