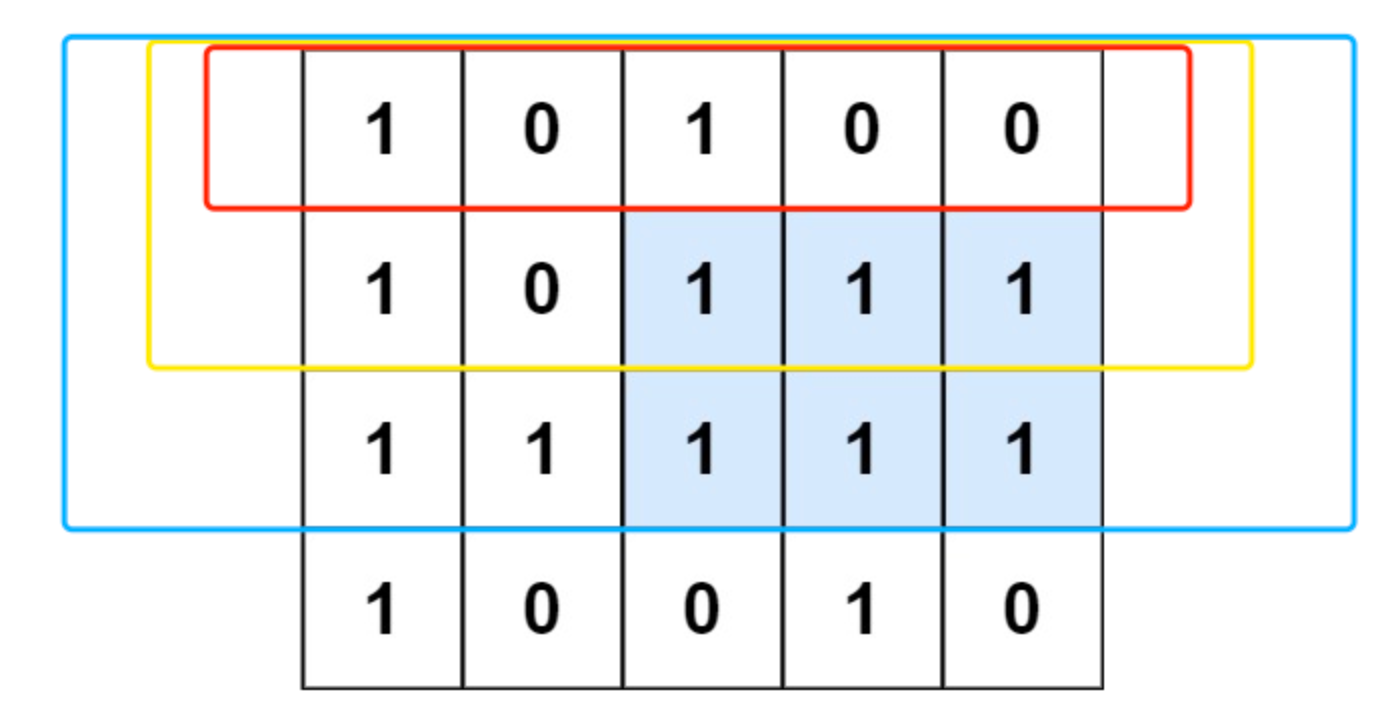
- 杨辉三角是二项式系数的典型应用
- 当 n 较大,且需要取模时,二项式系数有两种计算方法:
- 一:递推公式,
- 二:逆
方法一:用递推公式计算二项式系数
public class BinomialCoefficient {
public static int calculate(int n, int k) {
if (k > n) {
return 0; // 如果 k 大于 n,则二项式系数为 0
}
int[][] dp = new int[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Math.min(i, k); j++) {
if (j == 0 || j == i) {
dp[i][j] = 1; // 当 j 为 0 或者 j 和 i 相等时,二项式系数为 1
} else {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; // 使用递推公式计算二项式系数
}
}
}
return dp[n][k];
}
public static void main(String[] args) {
int n = 5;
int k = 2;
int coefficient = calculate(n, k);
System.out.println("Binomial Coefficient C(" + n + ", " + k + ") = " + coefficient);
}
}
方法二:用逆计算二项式系数
public class InverseBinomialCoefficient {
public static int calculate(int coefficient, int n) {
for (int k = 0; k <= n; k++) {
if (binomialCoefficient(n, k) == coefficient) {
return k; // 找到与给定系数相符的 k 值,返回结果
}
}
return -1; // 如果没有找到匹配的 k 值,返回 -1 表示未找到
}
// 计算二项式系数的方法,与前面提到的计算方法类似
public static int binomialCoefficient(int n, int k) {
if (k > n) {
return 0;
}
int[][] dp = new int[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Math.min(i, k); j++) {
if (j == 0 || j == i) {
dp[i][j] = 1;
} else {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
}
}
return dp[n][k];
}
public static void main(String[] args) {
int coefficient = 10;
int n = 5;
int k = calculate(coefficient, n);
if (k != -1) {
System.out.println("For binomial coefficient C(" + n + ", x) = " + coefficient + ", x = " + k);
} else {
System.out.println("No matching value of k found for coefficient " + coefficient);
}
}
}
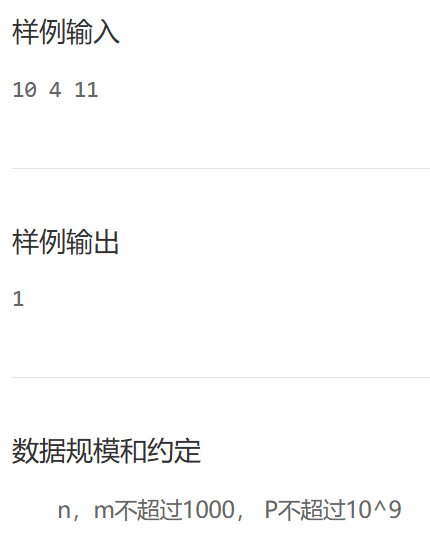
一、试题 算法训练 组合数取模
分析:
- 组合数简单理解为从装有 n 个不同球的盒子里抽 m 个球,有多少种情况(顺序不要求)
- 使用递推公式计算,
- 套用代码,再取余
- 特殊情况:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n=scanner.nextInt();
int m=scanner.nextInt();
int p=scanner.nextInt();
int coefficient=calculate(n,m,p);
System.out.println(coefficient);
}
public static int calculate(int n, int m,int p) {
if (m > n) {
return 0; // 如果 m 大于 n,则二项式系数为 0
}
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Math.min(i, m); j++) {
if (j == 0 || j == i) {
dp[i][j] = 1; // 当 j 为 0 或者 j 和 i 相等时,二项式系数为 1
} else {
dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j])%p; // 使用递推公式计算二项式系数
}
}
}
return dp[n][m];
}
}
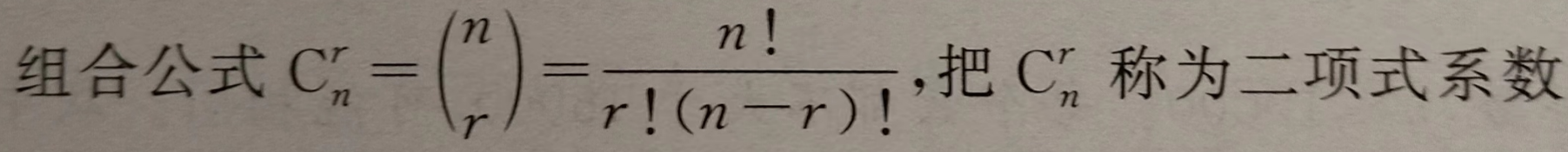
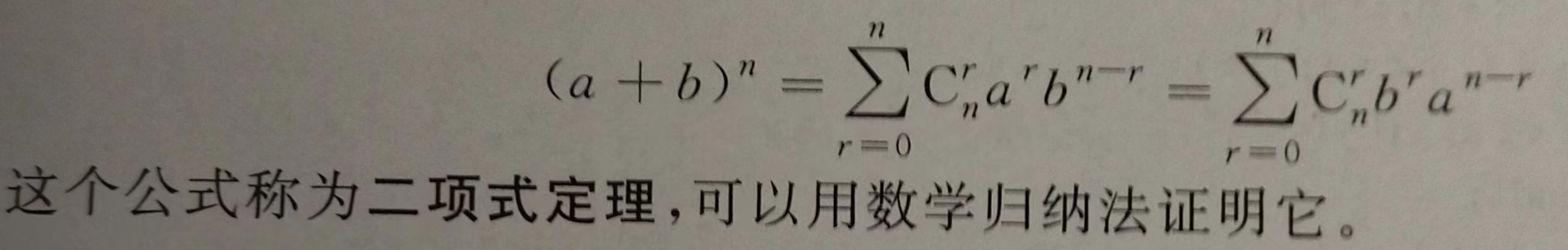






![[01] Vue2学习准备](https://img-blog.csdnimg.cn/direct/eb8c749700cc493b96ad7446db10b40b.png)