题解37-42

101. 对称二叉树 - 力扣（LeetCode）

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

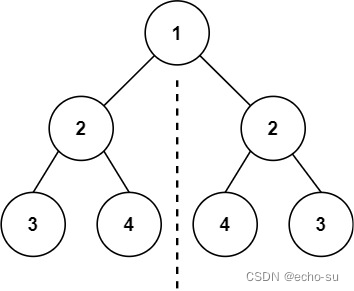
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

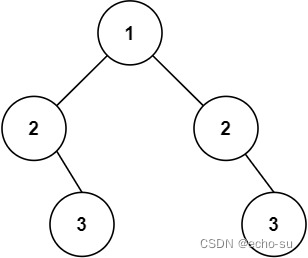
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

思路:

运用递归来判断,我们只需要判断一个子结构就行,对于一个子结构的判断逻辑

如果当前节点p和q,有一个为nullptr,只有两个都为nullptr才行
递归判断只有当前p和q的val相等,并且对应相等才行

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool dfs(TreeNode *left, TreeNode *right)
    {
        if(left == nullptr || right == nullptr)
            return left == right;
        return left->val == right->val && dfs(left->right, right->left) && dfs(left->left, right->right);
    }
    bool isSymmetric(TreeNode* root) {
        return dfs(root->left, root->right);
    }
};

102. 二叉树的层序遍历 - 力扣（LeetCode）

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

示例 1：

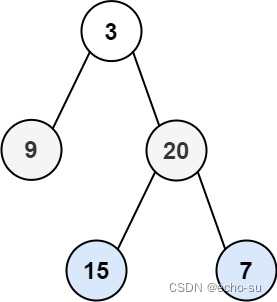
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000

思路:

宽度优先搜索,我们只需要对队列不断遍历即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        queue<TreeNode*> q;
        if(root == nullptr)
            return {};
        q.push(root);
        while(q.size())
        {
            vector<int> level;
            int n = q.size();
            while(n --)
            {
                auto p = q.front();
                level.push_back(p->val);
                q.pop();
                if(p->left)
                    q.push(p->left);
                if(p->right)
                    q.push(p->right);
            }
            res.push_back(level);

        }
        return res;
    }
};

104. 二叉树的最大深度 - 力扣（LeetCode）

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

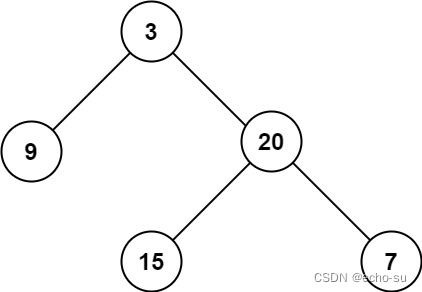
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

树中节点的数量在 [0, 104] 区间内。
-100 <= Node.val <= 100

思路:

这道题也是通过递归来实现,我这里参考了灵神的两种写法,分别是全局的答案和局部的答案

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = 0;
    void dfs(TreeNode *node, int cnt)
    {
        if(node == nullptr)
            return;
        cnt ++;
        ans = max(ans, cnt);
        dfs(node->left, cnt);
        dfs(node->right, cnt);
    }
    int maxDepth(TreeNode* root) {
        dfs(root, 0);
        return ans;
    }
};

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

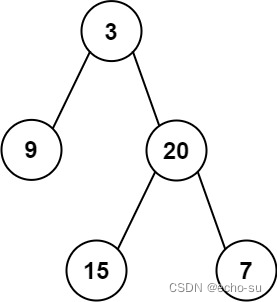
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

思路:

递归的思路,我们先通过前序遍历找到根节点,然后根据前序遍历在中序遍历中的位置确定左子树的长度,然后再确定右子树的长度,下面的参数做一下说明 $pl 和 p r$ 表示先序遍历的 $l e f t$ 和 $r i g h t$ ,然后哈希表是用来找出先序遍历在中序遍历中的下标,用于我们定义长度用的,注意一下数的长度就行

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> pos;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        for(int i = 0; i < inorder.size(); i ++)
            pos[inorder[i]] = i;
        return build(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
    }
    TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pl, int pr, int il, int ir)
    {
        if(pl > pr) return nullptr;
        
        auto root = new TreeNode(preorder[pl]);
        int k = pos[root->val];//找出映射位置前序第一个对应中序的下标为k,左子树就是
        root->left = build(preorder, inorder, pl + 1, pl + 1 + k - 1 - il, il, k - 1);
        root->right = build(preorder, inorder, pl + 1 + k - 1 - il + 1, pr, k + 1, ir);
        return root;

    }
};

114. 二叉树展开为链表 - 力扣（LeetCode）

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

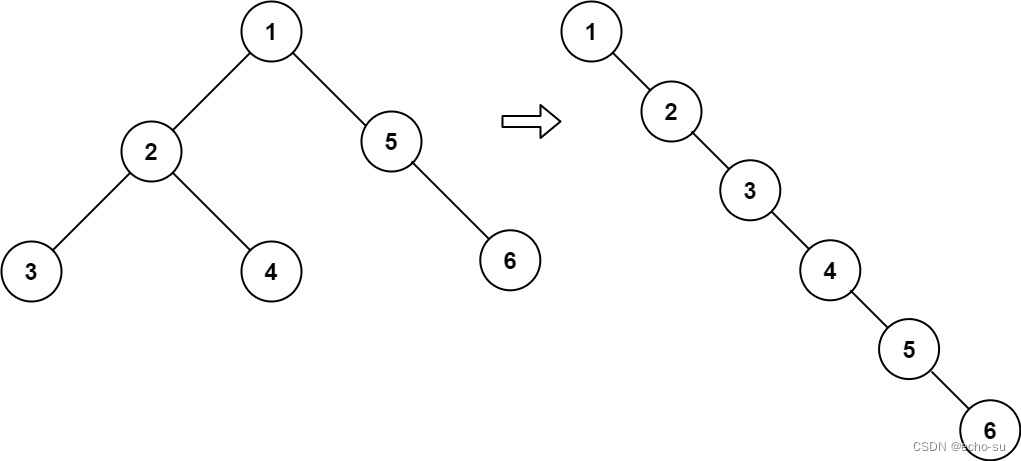
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

**进阶：**你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

这道题目考察了对树和链表的操作。

思路:

我们先定义右链：指一棵子树最右侧的路径。
我们从根节点开始迭代，每次将当前节点的左子树的右链，插入当前节点的右链，如下所示：

1
/
2 5
/ \
3 4 6
1

2
/
3 4

5

6
1

2

3

4

5

6

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        auto now = root;
        while(now)
        {
            if(now->left)
            {
                TreeNode *p = now->left;
                while(p->right) p = p->right;
                p->right = now->right;
                now->right = now->left;
                now->left = nullptr;
            }
            now = now->right;
        }
    }
};

121. 买卖股票的最佳时机 - 力扣（LeetCode）

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 105
0 <= prices[i] <= 104

思路:

这道题思路就是遍历,第一个 $_ min\_$ 是为了解决第一天的特判问题

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        int res = 0;
        for(int i = 0, min_ = INT_MAX; i < n; i ++)
        {
            res = max(res, prices[i] - min_);
            min_ = min(min_, prices[i]);
        }
        return res;
    }
};