C# CAD2016 判断多边形的方向正时针或逆时针旋转

news2024/11/26 21:52:49

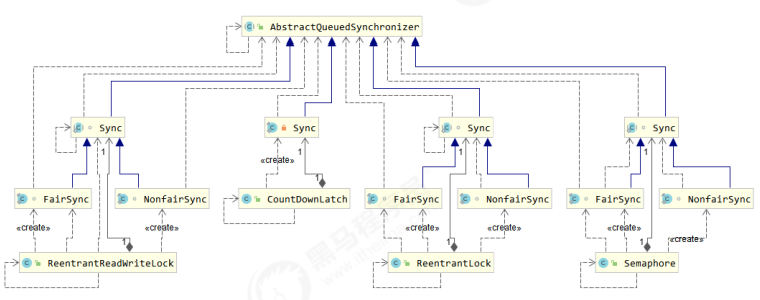
方法一：基于相邻顶点相对位置判断顺时针排列

// 计算当前子序列是否为顺时针排列
for (int i = 1; i < outerPoints.Count; i++)
{
    int index = (startVertexIndex + i) % outerPoints.Count;
    int prevIndex = (startVertexIndex + i - 1) % outerPoints.Count;

    Point2d currentPoint = outerPoints[index];
    Point2d prevPoint = outerPoints[prevIndex];

    // 判断当前顶点是否位于前一个顶点的顺时针方向（右侧和下方）
    if (currentPoint.X <= prevPoint.X || (currentPoint.X == prevPoint.X && currentPoint.Y <= prevPoint.Y))
    {
        isClockwiseFromNorthwest = false;
        break;
    }
}

此方法通过检查每个顶点与其前一个顶点的关系，逐个确定多边形顶点是否按顺时针顺序排列。但这种方法只适用于局部判断，并且依赖于已知的起始顶点是西北角。

方法二：利用Shoelace公式计算有符号面积判断顺时针排列

int j = outerPoints.Count - 1;
double sum = 0;

for (int i = 0; i < outerPoints.Count; i++)
{
    sum += (outerPoints[j].X - outerPoints[i].X) * (outerPoints[j + 1].Y + outerPoints[i].Y);
    j = i;
}

if (sum > 0)
{
    isClockwiseFromNorthwest = false;
}
else
{
    isClockwiseFromNorthwest = true;
}

此方法通过Shoelace公式计算整个多边形的有符号面积来判断其方向，对于凸/凹多边形都适用，不依赖于特定的起始顶点信息。不过要注意，在实际应用中可能需要额外处理边界情况和特殊情况，如所有点共线等情况。