A. Sasha and the Beautiful Array

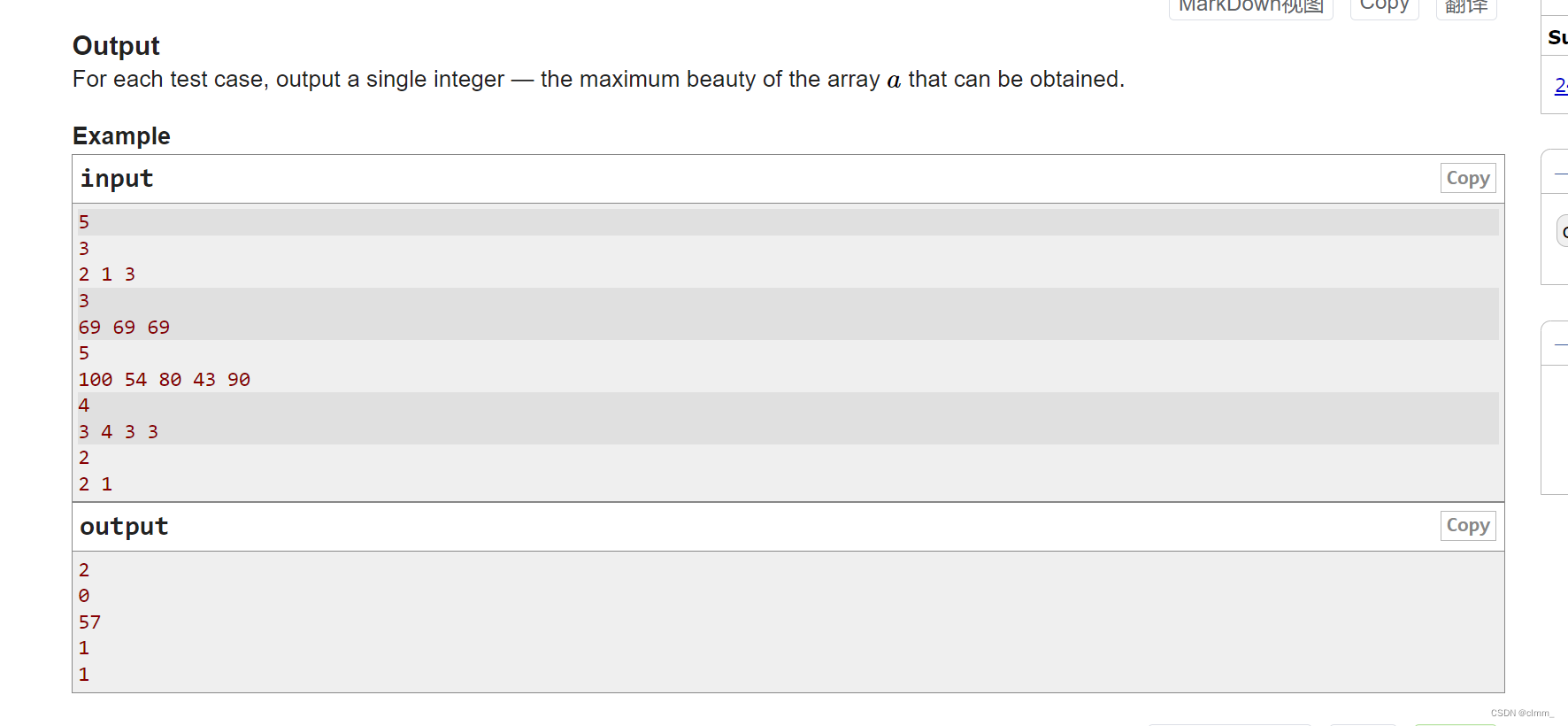
分析:说实话,打比赛的时候看到这题没多想,过了一下样例发现将数组排序一下就行,交了就过了。刚刚写题解反应过来,a2-a1+a3-a2.....an-a(n-1) = an - a1,所以最后结果只取决于最大和最小的差。
int a[N];
void solve() {
int n; cin >> n;
rep(i, 1, n) cin >> a[i];
sort(a + 1, a + 1 + n);
int ans = 0;
rep(i, 2, n) {
ans += a[i] - a[i - 1];
}
cout << ans << endl;
}B. Sasha and the Drawing


分析:同样是过了第三个样例发现,只需要涂第一排和最后一排就行了,而且(1,1)和(1,n)要放在最后涂,因为先把别的格子涂满,每涂一个格子贡献+2,最后(1,1)和(1,n)这两个格子,每格贡献+1。
void solve() {
int n, k; cin >> n >> k;
int cnt = 4 * n - 2 - 2;
int d = k - cnt;
//tans;
if (d <= 0) {
if (k % 2) k++;
cout << k / 2 << endl;
}
else {
cout << cnt / 2 + d << endl;
}
}C. Sasha and the Casino


题意:每次下注y元,输了失去y元,赢了得到y*k元(也就是增加y*(k-1)元,如果加上下注的本金就算y*k元了)。
sasha不会连续输x次,也就是说如果连输x次,第x+1次必赢。
最后问,sasha能不能依靠赌博,来无限赢钱。
反思:做题的时候陷入一个误区,我前x场都输掉,然后第x+1场把剩下的钱全下注了,那么只要本金足够,这样不是很好赢钱吗?其实不是的,因为赌场不会一直让你前x场全输的,可能会在第x-1场让你赢一下,“刷新”一下你输的场数。还有一个很需要反思的事情,明明之前一直提醒自己,做题要勤列公式,可是当时脑抽了一直在钻牛角尖没列公式。。。
分析:
我们要保证每一轮赢的钱>输的钱,这样我们才能赢到无限的钱。一轮的结尾是赢的那一把,因为我们一旦赢了,就“刷新”了我们输的场数。
上面说了,在第1~x场,赌场可能会让你赢一场,而如果1~x场全输了,第x+1场必赢。
我们可以得出一个结论:1~x+1场,我们必赢一场!这是重点
一轮中,当我们在第i场(1<=i<=x+1)赢了,说明第1 ~ i-1场是输的,因此我们在第i场赢的前要大于前i-1场输的钱。
可以得到公式
有
,yi表示第i场下注的金额
sum =
,sum表示输的金额
win = yi*(k-1),win表示在第i场赢的金额
win - sum > 0
yi > sum / (k-1)
说明,我们第i场的下注金额yi至少是 sum/(k-1)+1。
而到了第i场我们还剩下 a-sum元,
因此得到了不等式,sum/(k-1) + 1 <= a-sum
int k, x, a;
void solve() {
cin >> k >> x >> a;
int sum = 0;
int f = 1;
rep(i, 1, x + 1) {
int y = sum / (k - 1) + 1;
if (y <= a - sum) {
//有钱下注。然后我们要假设输掉这场
sum += y;
}
else {
//没钱下注,就算赢了也没用
f = 0;
break;
}
}
//tans;
if (!f) cout << "NO" << endl;
else cout << "YES" << endl;
}