今天总结一下回溯法以来做过的这些题,我又发现一个困扰了我的问题,就是在491. 非递减子序列、46. 全排列、47. 全排列 II中都有涉及到用哈希法,去记录曾经用过的元素,下面来总结一下吧。
首先得知道,为什么会用到哈希法?
为什么会用到哈希法?
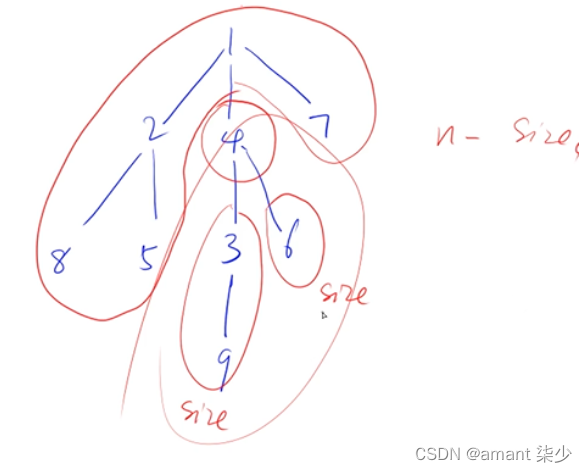
在491. 非递减子序列问题中,是因为集合中有相同的元素,而结果又不能出现相同的组合,如本题的示例1 [4,6,7,7]中,当4与倒数第二个7组合时,一个答案为[4,7],而下一个,与倒数第一个7则不能再组合了,即不能出现两个[4,7],借代码随想录里的图来理解,就是同一层不能重复使用相同的数字,如图: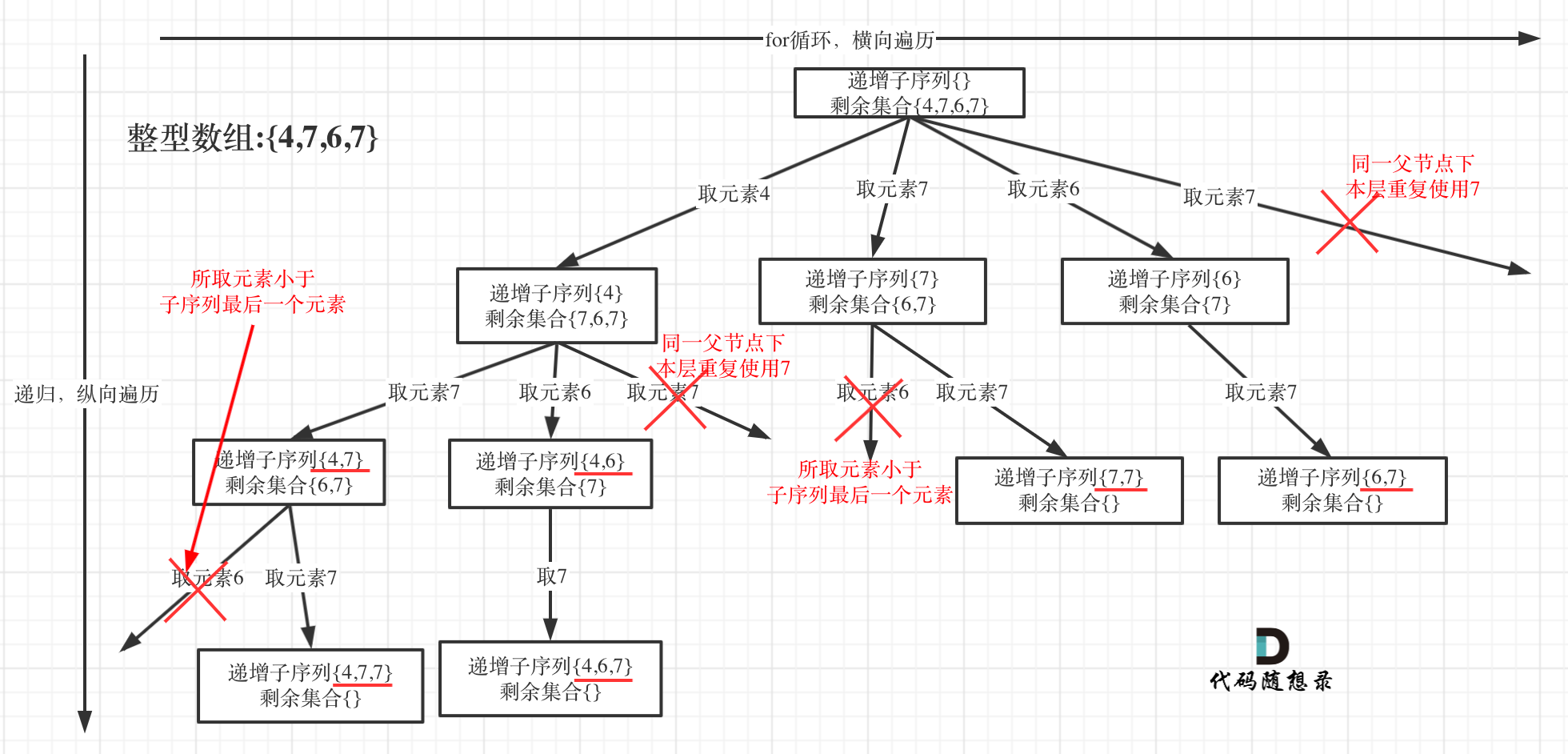
而这时,就可以利用一个哈希表,来保存每一层使用过哪些元素,注意这里的每一层这个要求,结合下面的代码理解一下:
非递减子序列代码:
public void backtracking(int[] nums, int startIndex) {
if(temp.size() >= 2) {
result.add(new ArrayList<>(temp));
}
Set<Integer> set = new HashSet<>(); // 在每一层递归中,设置一个Set哈希表,记录这一层使用过哪些元素
for(int i = startIndex; i < nums.length; i++) {
// 解决递增以及重复的问题
if(!temp.isEmpty() && (nums[i] < temp.get(temp.size() - 1)) || set.contains(nums[i])) {
continue;
}
temp.add(nums[i]);
set.add(nums[i]);
backtracking(nums, i + 1);
temp.remove(temp.size() - 1);
}
}
而在全排列问题中,则不是记录每一层,而是记录某条树枝上(即整个递归中)哪些元素使用过,例如46. 全排列中的示例1的数据[1,2,3],由于排列的特点,for循环每次都从0开始,但是要保证不能重复选某个元素,所以要用哈希表来记录,哪些数字用了,哪些没有,下面是代码,重在理解“某条树枝上(即整个递归中)哪些元素使用过”。
全排列代码:
class Solution {
List<Integer> temp = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
boolean[] table = new boolean[21]; // 哈希表,记录整个递归中使用过的元素
public List<List<Integer>> permute(int[] nums) {
backtracking(nums);
return result;
}
public void backtracking(int[] nums) {
if(temp.size() == nums.length) {
result.add(new ArrayList<>(temp));
return;
}
for(int i = 0; i < nums.length; i++) {
// 去重操作
if(!temp.isEmpty() && table[nums[i] + 10]) {
continue;
}
temp.add(nums[i]);
table[nums[i] + 10] = true; // 设置哈希表,使用过的元素记录
backtracking(nums);
temp.remove(temp.size() - 1); // 回溯
table[nums[i] + 10] = false; // 回溯之后,使用过的记录也清空
}
}
}
而这道题的升级版:47. 全排列 II,由于出现了重复元素,为了还能全排列,设计哈希表时,就不是记录值而是记录使用过的元素的位置了,因为排列时,使用的数字位置不同,排列也是不同的,所以对于全排列 II,哈希表记录的是整个递归中,使用的是哪个位置的元素,下面是代码:
全排列 II代码:
class Solution {
List<Integer> temp = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);// 排序是为了后面的组间去重
boolean[] used = new boolean[nums.length]; // 其实这个放在全局变量也行
backtracking(nums, used);
return result;
}
public void backtracking(int[] nums, boolean[] used) {
if(temp.size() == nums.length) {
result.add(new ArrayList<>(temp));
return;
}
for(int i = 0; i < nums.length; i++) {
if(used[i]) { // 判断当前这个位置的元素是否在前面的递归中使用过,如果使用过,则排列下面的元素
continue;
}
temp.add(nums[i]);
used[i] = true;
backtracking(nums, used);
temp.remove(temp.size() - 1);
used[i] = false; // 回溯不要忘了把丢弃的元素也设置为“未使用”
while(i + 1 < nums.length && nums[i +1] == nums[i]) {// 去重操作
i++;
}
}
}
}
总结
可以看出来,其实用上哈希法,就是两种情况,要么是要判断同一层是否使用过,要么是要判断整个递归中是否使用过,对应就是哈希表定义的地方不同,要判断同一层是否使用过,哈希表定义在递归函数里;要判断整个递归中是否使用过,哈希表定义在全局变量中或者定义在递归函数之外。