朋友们、伙计们,我们又见面了,本期来给大家解读一下位图、布隆过滤器、哈希分割,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成!
C 语 言 专 栏:C语言:从入门到精通
数据结构专栏:数据结构
个 人 主 页 :stackY、
C + + 专 栏 :C++
Linux 专 栏 :Linux

目录
1. 位图
1.1 概念
1.2 简单实现
1.3 应用
2. 布隆过滤器
2.1 布隆过滤器的提出
2.2 布隆过滤器的概念
2.3 布隆过滤器的插入
2.4 布隆过滤器的查找
2.5 布隆过滤器的删除
2.6 布隆过滤器的优缺点
3. 哈希分割
3.1 哈希分割的应用
4. 布隆过滤器的应用
1. 位图
1.1 概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用
来判断某个数据存不存在的。位图参考文档
1.2 简单实现
【题目】:给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中?
解决该题有以下三种方法:
1. 暴力求解(O(N))
2. 排序(O(N*logN)) + 二分(logN)
3. 位图解决
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。
首先我们得找到key在位图中对应的位置,那么这个位置与key的映射关系是怎么样的呢?
首先我们得找到key在第几个整型中,所以需要用key/32获取在第几个整型中,用i来表示。然后还需要知道在整型中的第几个比特位,所以需要用key%32,用j来表示。然后根据对应比特位的值是0还是1来判断在不在。
如果我们要向位图中进行插入,那么需要找到key对应的比特位,然后将1左移j位,然后与该位置按位或,即可将对应的比特位改为1。
如果需要删除,那么就将1左移j位后的值按位取反,然后与对应的位置按位与,即可将对应的比特位改为0。
代码实现:
#pragma once #include <vector> namespace ywh { //位图 //N是需要多少比特位 template<size_t N> class bit_set { public: bit_set() { _bits.resize(N / 32 + 1, 0); } //插入 void set(size_t x) { size_t i = x / 32; //第几个整型 size_t j = x % 32; //第几个比特位 _bits[i] |= (1 << j); //对应的比特位改为1 } //删除 void reset(size_t x) { size_t i = x / 32; //第几个整型 size_t j = x % 32; //第几个比特位 _bits[i] &= (~(1 << j)); //对应的比特位改为0 } //判断 bool test(size_t x) { size_t i = x / 32; //第几个整型 size_t j = x % 32; //第几个比特位 return _bits[i] & (1 << j); } private: vector<int> _bits; }; }
1.3 应用
1. 给定100亿个整数,设计算法找到只出现一次的整数?
在位图中我们表示一个数存在,则对应的比特位是1,那么我们可以使用两个比特位表示一个数出现的次数:
出现0次 -> 00
出现1次 -> 01
出现2次及以上 -> 10
那么在插入中就需要做一改进
在插入时对应的是00,那么就改为01,如果是01,就改为10。
代码实现:
namespace count_num { template<size_t N> class Oncebitset { public: //插入 void set(size_t x) { size_t i = x / 32; //第几个整型 size_t j = x % 32; //第几个比特位 if (_bs1[x] == false && _bs2[x] == false) //00 { _bs2.set(x); //对应的比特位改为1 //01 } else if (_bs1[x] == false && _bs2[x] == true) //01 { _bs1.set(x); //对应的比特位改为1 _bs2.reset(x); //对应的比特位改为0 //10 } } void PrintOnce() { for (size_t i = 0; i < N; i++) { if (_bs1.test(i) == false && _bs2.test(i) == true) { cout << i << endl; } } cout << endl; } private: bitset<N> _bs1; bitset<N> _bs2; }; }
2. 给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?将这两个文件分别映射到位图中,若一个值在这两个位图中都存在,那么便是交集。
3. 位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数同样的还是使用两个比特位来表示一个数出现的次数:
出现0次 -> 00
出现1次 -> 01
出现2次 -> 10
出现3次及以上 -> 11
2. 布隆过滤器
2.1 布隆过滤器的提出
1. 用哈希表存储用户记录,缺点:浪费空间。
2. 用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理了。
3. 将哈希与位图结合,即布隆过滤器
2.2 布隆过滤器的概念
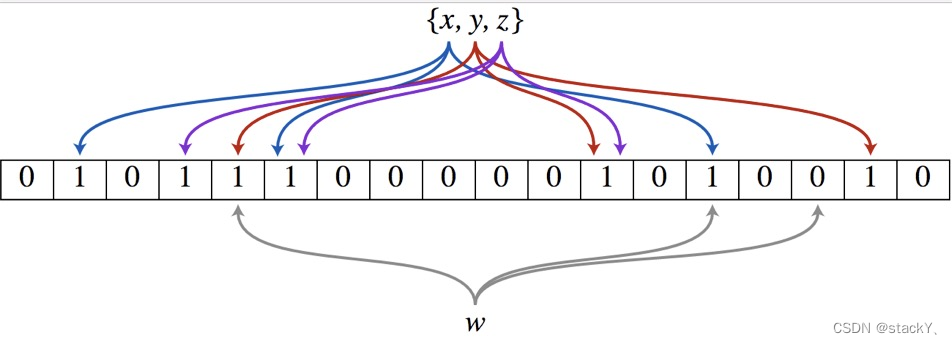
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”。它是用多个哈希函数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
从上图也不难看出布隆过滤器存在一定的误判,例如:x和w映射的其中一个位置冲突,y和w映射的其中一个位置也冲突。因此布隆过滤器判断一个值不存在是准确的,判断一个数存在是不准确的。
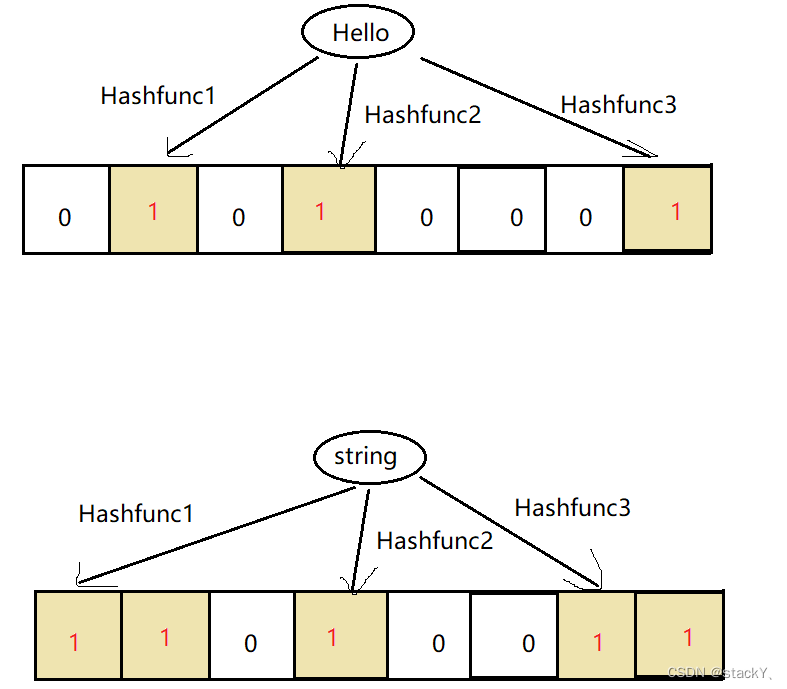
2.3 布隆过滤器的插入
布隆过滤器的目的就是为了在位图的基础上处理一些非整型的数据,那么根据三种对应的映射关系将对应位置的比特位改为1即可。
//三种对应的映射关系 struct BKDRHash { size_t operator()(const string& key) { size_t hash = 0; for (auto e : key) { hash *= 31; hash += e; } return hash; } }; struct APHash { size_t operator()(const string& key) { size_t hash = 0; for (size_t i = 0; i < key.size(); i++) { char ch = key[i]; if ((i & 1) == 0) { hash ^= ((hash << 7) ^ ch ^ (hash >> 3)); } else { hash ^= (~((hash << 11) ^ ch ^ (hash >> 5))); } } return hash; } }; struct DJBHash { size_t operator()(const string& key) { size_t hash = 5381; for (auto ch : key) { hash += (hash << 5) + ch; } return hash; } }; //布隆过滤器 template<size_t N, class K = string, class Hashfunc1 = BKDRHash(), class Hashfunc2 = APHash(), class Hashfunc3 = DJBHash()> class Bloom_filter { public: //插入 void Set(const K& key) { size_t hash1 = BKDRHash()(key) % N; size_t hash2 = APHash()(key) % N; size_t hash3 = DJBHash()(key) % N; _bits.set(hash1); _bits.set(hash2); _bits.set(hash3); } private: bitset<N> _bits; };
2.4 布隆过滤器的查找
查找这里就存在误判了,如果判断这个值不存在,那么对应的映射位置的比特位为0,如果判断一个值存在,那么对应的位置的比特位为1,但是这些对应位置是一对多的关系,所以就会出现误判。
//判断 bool Test(const K& key) { size_t hash1 = BKDRHash()(key) % N; if (_bits.test(hash1) == false) return false; size_t hash2 = APHash()(key) % N; if (_bits.test(hash2) == false) return false; size_t hash3 = DJBHash()(key) % N; if (_bits.test(hash2) == false) return false; //存在误判 return true; }
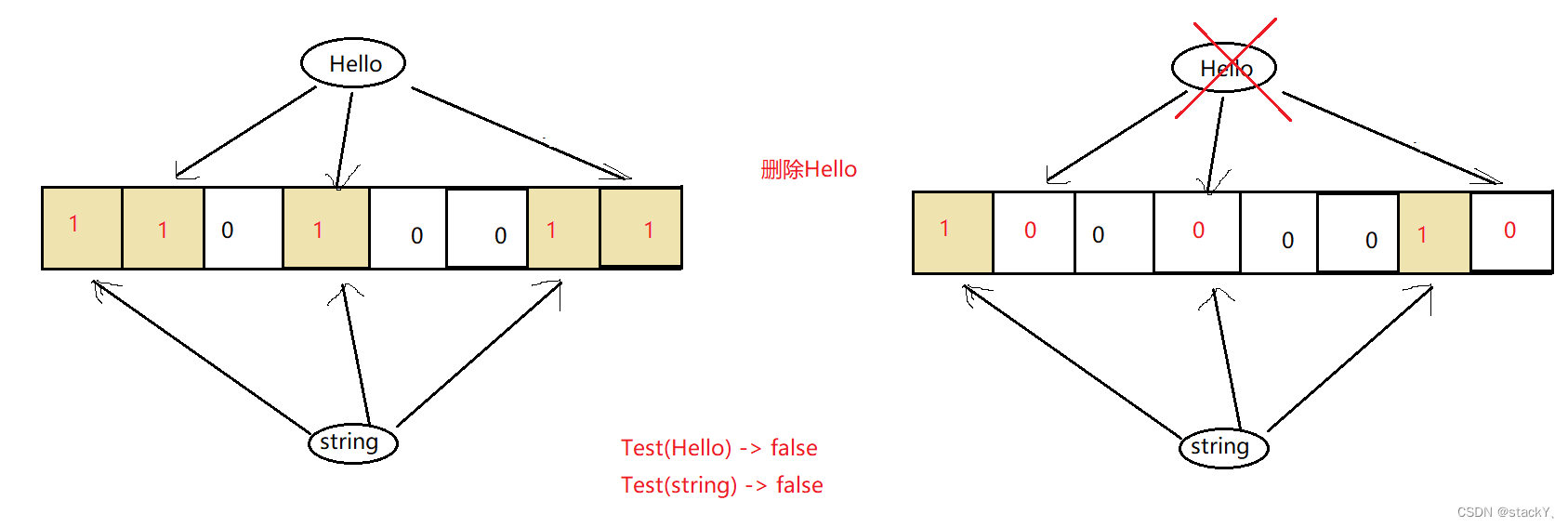
2.5 布隆过滤器的删除
布隆过滤器其是不支持删除的,因为映射对应的比特位并不是一对一的关系,很有可能两个key对应位置其中一个或两个比特位是一样的,那么你要删除其中一个值,肯定要将这个值对应的比特位全部置为0,此时就会出现问题,另外一个值指向的比特位也被置为了0,也会被删除掉。但是可以通过引用计数的方式来实现一个删除的接口,记录映射在该比特位上key的个数,如果只有一个可以直接置为0,如果有多个不能置为0。
2.6 布隆过滤器的优缺点
优点:
1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
2. 哈希函数相互之间没有关系,方便硬件并行运算
3. 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
4. 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
5. 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
缺点:
1. 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
2. 不能获取元素本身
3. 一般情况下不能从布隆过滤器中删除元素
4. 如果采用计数方式删除,可能会存在计数回绕问题
3. 哈希分割
哈希分割也叫哈希切分,所谓的哈希分割就是通过哈希思想,将大量的数据划分为具有类似属性的小块数据,例如:将一整个大的文件分成具有不同属性的若干个小文件,然后对这些小文件进行操作。
3.1 哈希分割的应用
例:给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址?
首先可以肯定的是这个文件是不能加载到内存中的,那么就可以根据哈希切分将这100G的大文件划分为100个小文件,然后加载到内存中进行操作:
① 通过哈希算法将每一个IP地址转化为一个整数i,然后取模100,存放到对应的i号文件中。
② 通过哈希切分之后的这些若干个小文件就可以加载到内存中,通过容器map来进行统计次数,从而找到出现次数最多的IP地址。
4. 布隆过滤器的应用
布隆过滤器适合处理一些非整形的数据,那么在一些情况下,布隆过滤器的作用还是很明显的:
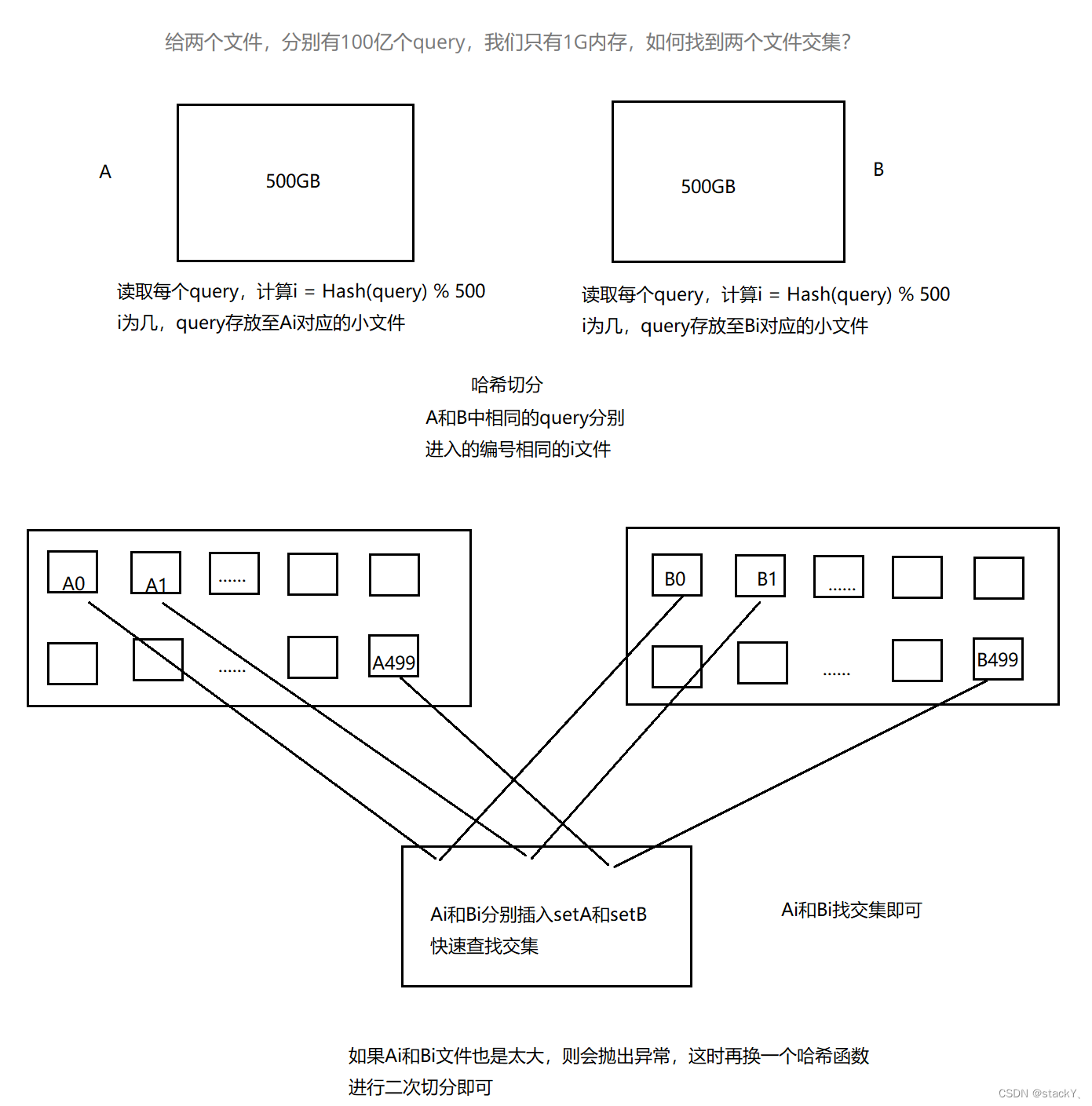
例:给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?
首先有100亿个query,假设一个query大小为50字节1GB 约等于 10亿字节
100亿个query的大小就是5000亿字节 约等于 500GB
有两个文件,总共1000GB的大小。
那么内存肯定是存不下的,所以我们首先想到的就是哈希切分:
① 通过哈希算法分别将这两个文件中的每一个query转化为一个整数i,然后取模500,存放到对应的Ai号文件和Bi号文件中。
② 通过哈希切分之后的这些若干个小文件就可以加载到内存中,然后将Ai文件对应的Bi文件加载到内存,分别插入到一个setA和setB中,再找交集。
注意:可能存在切分之后的这些小文件大小还是不足以放到内存中,那么可以再对这个小文件换一种哈希算法再次分割
朋友们、伙计们,美好的时光总是短暂的,我们本期的的分享就到此结束,欲知后事如何,请听下回分解~,最后看完别忘了留下你们弥足珍贵的三连喔,感谢大家的支持!