1.题目

给定一颗树，树中包含 $n$ 个结点（编号 $1\sim n$）和 $n-1$ 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式
第一行包含整数 $n$，表示树的结点数。

接下来 $n-1$ 行，每行包含两个整数 $a$ 和 $b$，表示点 $a$ 和点 $b$ 之间存在一条边。

输出格式
输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值

数据范围
$1\le n\le 10^5$

输入样例：

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

2.基本思想

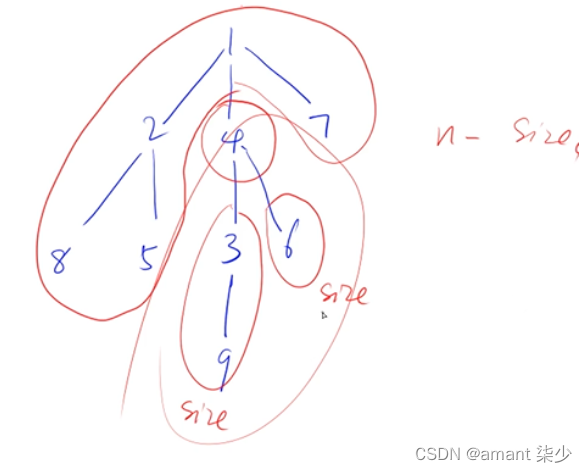
（数组建立邻接表） 树的dfs

//邻接表
int h[N], e[N * 2], ne[N * 2], idx;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

树的bfs模板

// 需要标记数组st[N],  遍历节点的每个相邻的便
void dfs(int u) {
    st[u] = true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!st[j]) {
            dfs(j);
        }
    }
}

• 本题的本质是树的dfs， 每次dfs可以确定以u为重心的最大连通块的节点数，并且更新一下ans。

也就是说，dfs并不直接返回答案，而是在每次更新中迭代一次答案。

• 在本题的邻接表存储结构中，有两个容易混淆的地方，一个是节点的编号，一个是节点的下标。
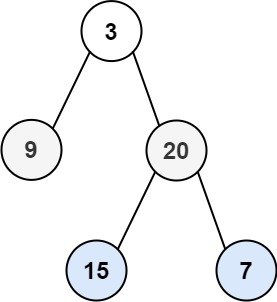
  节点的编号是指上图所画的树中节点的值，范围是从1~n。在本题中，每次输入的a和b就是节点的编号，编号用e[i]数组存储。
  节点的下标指节点在数组中的位置索引，数组之间的关系就是通过下标来建立连接，下标用idx来记录。idx范围从0开始，如果idx==-1表示空。
  e[i]的值是编号，是下标为i节点的编号。
  ne[i]的值是下标，是下标为i的节点的next节点的下标。
  h[i]存储的是下标，是编号为i的节点的next节点的下标，比如编号为1的节点的下一个节点是4，那么我输出e[h[1]]就是4。

3.代码实现

import java.util.Scanner;

public class Main {
    static int N = 100010;
    static boolean st[] = new boolean[N];
    static int[] h = new int[N], e = new int[N*2], ne = new int[N*2];
    static int n, idx, ans = N;

   static void init() {
        for (int i = 0; i < N; i++) h[i] = -1;
    }

    static private void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }

    //返回以 u 为根的子树的点的数量
    private static int dfs(int u) {
        st[u] = true;
        int sum = 1, res = 0;// res:删除根后 每个连通块的最大值
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (!st[j] ) {
                int s = dfs(j);//当前子树大小
                res = Math.max(res, s);
                sum += s;
            }
        }
        res = Math.max(res, n - sum);
        ans=Math.min(ans,res);
        return sum;
    }

    public static void main(String[] args) {
       init();
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        for (int i = 0; i < n-1; i++) {
            int a = sc.nextInt(), b = sc.nextInt();
            add(a, b);
            add(b, a);
        }
        dfs(1);
        System.out.println(ans);
    }
}