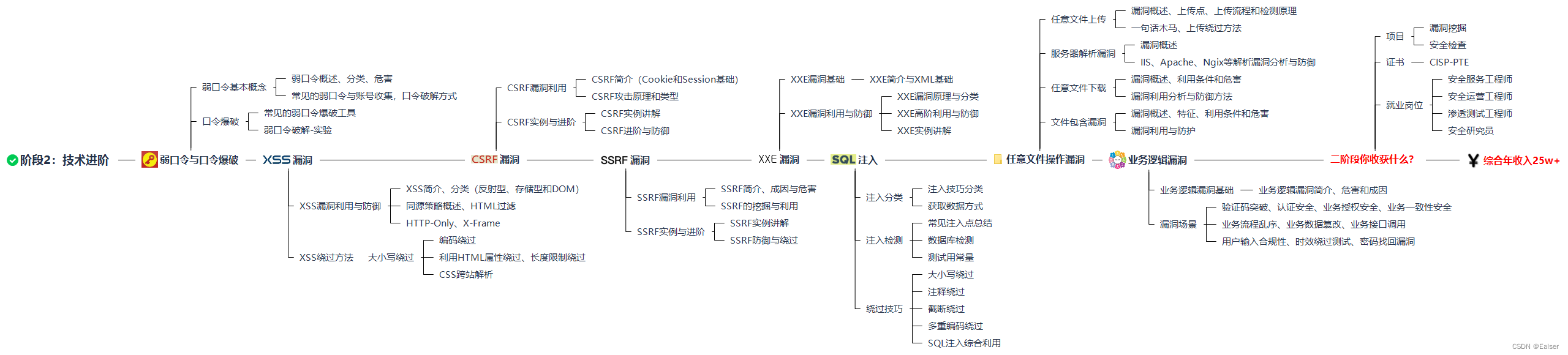
梯形积分

设f(x)在[a,b]上连续，若要计算其积分，则
$${\int }_a^{b}f(x)dx=F(b)-F(a)$$
其中F(x)为f(x)的原函数，但是计算机直接计算出该积分函数比较困难，因此需要近似求解。梯形积分使用函数的区间边界点作梯形进行计算，即
$${\int }_a^{b}f(x)dx\approx \frac{(f(a)+f(b))(b-a)}{2}$$
当[a,b]区间比较小时，这个误差就比较小，对于[a,b]区间比较大的情况，普通的梯形积分就不再适用，需要对梯形积分进行复化。

复化梯形积分

复化梯形积分就是在区间[a,b]上进行m次划分，每次划分得到n个子区间，然后计算每个子区间的梯形积分，最后将这m个梯形积分相加，得到整个区间的梯形积分。
假设[a,b]区间被划分为n个区间，h=(b-a)/n，$x_k=a+kh(k=0,\cdots ,n)$
$$\begin{gathered} {\int }_a^{b}f(x)dx\approx \sum _{k=1}^n\frac{h}{2}[f(x_{k-1}+f(x_k))] \\ =\frac{h}{2}[f(a)+2\sum _{k=1}^{n-1}f(x_k)+f(b)] \end{gathered}$$

误差分析

复化梯形积分要划分为多少个区间才合适呢？显然需要做一个误差控制，但是问题就在于如何判断复化梯形积分与实际积分值的误差，使用梯形积分的原因就是因为原本的积分不容易求出来，所以直接比较是不可以的，此处需要使用到事后误差分析，即区间继续增加划分数量时，积分值变化小于某个值时即可认为此时的积分与实际的误差小于一定范围。
复化梯形积分的余项可以表示为:
$$\begin{gathered} R[f]=\sum _{k=1}^n[-\frac{h^3}{12}{f}^{\prime \prime }({\xi }_k)] \\ =-\frac{h^2}{12}(b-a)\frac{{\sum }_{k=1}^n{f}^{\prime \prime }({\xi }_k)}{n} \\ =-\frac{h^2}{12}(b-a)f^{\prime \prime }(\xi )(\xi \in (a,b)) \\ =-\frac{(b-a{)}^3}{12n^2}{f}^{\prime \prime }(\xi )(\xi \in [a,b]) \end{gathered}$$
因此，要求梯形积分与实际积分值小于$ϵ$，则其余项小于$ϵ$：
$$\begin{gathered} I(f)-T_n(f)=-\frac{b-a}{12}{h}^2{f}^{\prime \prime }(\xi ) \\ I(f)-T_{2n}(f)=-\frac{b-a}{12}(h/2{)}^2{f}^{\prime \prime }(\eta ) \end{gathered}$$
两者可以近似为：
$$I(f)-T_n(f)\approx 4[I(f)-T_{2n}(f)]$$
因此若有
$$T_{2n}(f)-T_n(f)<3ϵ$$
即可等价为
$$I(f)-T_{2n}(f)<ϵ$$

代码实现

#include<iostream>
#include<cmath>
#include<iomanip>//这个头文件仅仅是用来设置cout的输出精度
#define abs(x) (x>0?x:-x)
using namespace std;
//梯形积分，传入参数为分段的n，积分下限a，积分上限b，对应的积分函数
double trapezium(int n,double a,double b,float(*f)(float x))
{
    double f_x=0.0f;
    double h=(b-a)/n;
    for (int i = 1; i < n; i++)
    {
        f_x+=f(a+i*h);//梯形公式的f(x_k)的累加和
    }
    f_x*=h;
    f_x+=(f(a)+f(b))*h/2;//根据n算出对应的复化梯形积分
    return f_x;
}
//直接在这里换函数，函数为sin(x)/x
float fx(float x)
{
    float result;
    float x_temp=((x==0)?1e-15:x);
    result=sin(x_temp)/x_temp;
    return result;
}
int main()
{
    double error=1e-6;//表示误差小于10^-6次方
    double a=0.0,b=2.0;//积分上下限
    int n=1;
    double f_x_n=(fx(a)+fx(b))*(b-a)/2;
    double f_x_2n;
    //可以在此处添加循环次数控制，防止误差无法缩小的情况出现
    while(true)
    {
        f_x_2n=trapezium(n*2,a,b,fx);//算T2n
        if(fabs(f_x_n-f_x_2n)<(error*3))
        {
            //cout<<n<<":trapezium error="<<fabs(f_x_n-f_x_2n)<<endl;
            cout << "梯形积分的误差为：" << fabs(f_x_n - f_x_2n) << endl;
            n*=2;
            break;
        }
        n+=1;
        f_x_n=trapezium(n,a,b,fx);//算Tn
    }
    cout<<"区间划分数量:n="<<n<<"，积分值为："<<std::setprecision(10)<<f_x_2n<<endl;
    return 0;
}

结果分析

运行程序后，被积函数为sin(x)/x，积分区间为[0,2]，为了达到$I(f)-T_{2n}(f)<10^{-6}$，需要将区间划分为382个小区间，此时采用事后误差估计法求得的$T_{2n}(f)-T_n(f)=2.98242\times 10^{-6}$。

为了验证事后误差估计法，采用Matlab进行计算，$I(f)$如下：

计算$T_{2n}(f)-I(f)$如下：

可以看出事后误差估计得到的结果符合期望。