前言

okey，欢迎来到2023年，那么在这里预祝各位在新的一年里面能够达到自己的预期。那么本篇博文也是作为我最近复习算法带来的一篇博文，那么这篇博文主要是针对图的那些基本算法，当然还是偏向竞赛方面。 (当然有些C++ 和 Python相差不大的代码统一给出C++的代码，看得懂，就没有切换语言了）当然这篇博文稍微有点长，大概2W个字左右吧，以后“水文”就不写了，要写就写详细一点的，长一点的。没办法，人都这么长，这个博文也也得长一点。

那么本篇博文一共有9个算法，一个常用套路。当然对于比较抽象的点，还是会有题目进行举例的。

同时先声明一下，文中提到的n,m分别是指带图中节点的个数和边的个数。并且我们对于节点的编号都是1~n,这个统一一下。同时g是图的意思，因为graph嘛

图的表示

邻接矩阵

关于咱们这个图的话，我们有两种方案进行存储，一个就是非常传统的方案，就是这个使用邻接矩阵，这个的话非常简单，没什么好说的。然后存有相无相图，都是一样的。

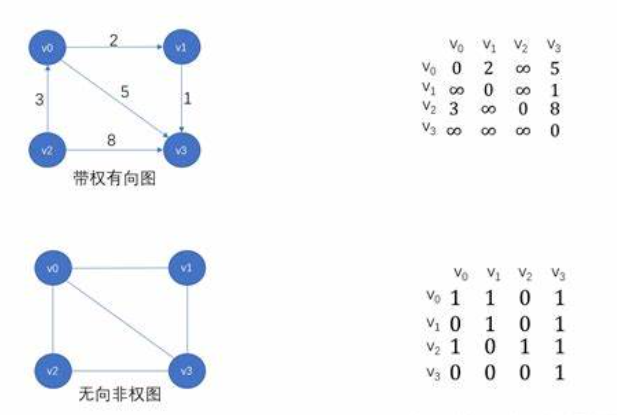
邻接表

之后的是我们第二种方式进行存储，也就是使用到咱们的这个邻接表。当然使用这个邻接表的话也是有非常多的一种方案。
但是总体的意思呢就是这样的：

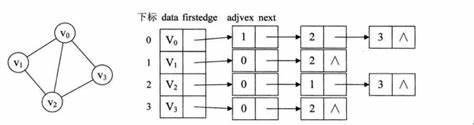
那么在这里的话，那么对于这个的话，我们也是有一个不错的，也在用的一个模板，只要维护三个数组就好了。当然你选择别的模板，如果是Python，Java，C++ 之类的，你直接用一个大数组，然后数组里面的每一个元素是这个表示边节点的一个数组也是可以的。按照图中的也可以，我们待会儿的模板是按照这个来的。

结构

okey，那么我们这边提供的模板，其实就是先前提到的用数组模拟链表，现在再用这个链表来串成一个图，仅此而已。那么好处的话，就是修改一些边方便，因为模拟的链表它具备，查询和修改的优势嘛。

int N = 100000;
int idx;
int e[N]; 
int w[N];
int ne[N]; 
int h[N] 初始化的值为-1

我们定义这几玩意来存储我们的一个图，那么接下来我来简单解释一下这几个数组的含义，这些数组数组的含义,以及这个idx的含义。

idx：表示的是我们对于这个图的节点进行一个编号，就是存储的时候，我们自己对这个存进去的节点进行一个简单的编号。
e[i]: 表示的是，我们自己定义的小标i,所对于图中那个节点的标号是啥。例如e[1]=5，表示我们这里面，定义的序号为1的玩意，对应的节点的编号为5.说白了，我们存进去的时候，是按照题目的输入存的顺序存储的，这个i就是idx。
ne[i]: 表示的是，当前我们定义的下标i,和他相连的下一个节点的下标（这个也是我们定义的）。假设，你想知道我们这边定义的下标为i的节点相连的那个节点在图中的序号，那么你就这样e[ne[i]]。
h[j]: 表示的是，在图中这个序号为j的节点，在我们这边定义的下标是多少，相当于存储头结点的数组。初始化的值为-1.
w[i]: 表示的就是我们这边编号为i的边的权重是多少，就是边权，然后的比较有意思的就是，假设i = h[j] ,i 是咱们图中j号节点在我们这边的下标，那么和他相连的第一个节点就是 k = e[ne[i]],然后这个w[i]的值，其实就是图中编号为j和k两个家伙之间的边的权重。原因的话看到下面咱们这个存储。

存储

明白了咱们上面的定义，那么咱们马上来看到如何去存储，加入这个边。
我们假设输入是这样的：

a b c
前面两个表示，图中的两个节点，c表示他们之间边权

这里使用的是头插法

void add(int a,int b,int c)
{
	e[idx] = b;
	w[idx] = c;
	ne[idx] = h[a];
	h[a] = idx++;
}

如果是无向图的话，那么在加入的时候就加入两次呗。

add(a,b,c);
add(b,a,c);

用这种结构的话，对于边的修改要快一点。当然一般可能也不会去动。

遍历

之后的话就是遍历，我们去通过我们刚刚的那个结构，去遍历出当前图中的每一个节点。如果要遍历的话我们就这样，当然这里有两个方法，一个是DFS，还有一个是BFS。

首先是DFS：
思路是一路走到底：
那么在这里还需要一个额外的数组这个是bool类型的

bool visited[N]

void dfs(int u)
{
	visited[u]=true;
	printf("%d",u);
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int j = e[i];
		if(!visited[j])
		{
			//遍历当前和这个节点相连的节点相连的节点
			dfs(j);
		}
	}
}

当然咱们还有这个BFS，那么对于这个BFS的话我们还需要一个队列，当然思路其实也是一样的。

bool visited[N]
queue<int> q;
void bfs(int u)
{
	q.push(u);
	visited[u]=true;
	while(q.size())
	{
		int t = q.front();
		printf("%d",t);
		for(int i=h[t];i!=-1;i=ne[i])
		//遍历和当前这个节点直接相连接的点
		{
			int j = e[i];
			if(!visited[j])
			{
				visited[j] = true;
				q.push(j);
			}
		}
	}
}

之后就是调用，因为我们这边编号是从1开始的，因此的话，调用就是：

bfs(1);
//dfs(1);

同样的如果你是想要确定图中a,b序号的点是不是联通的，那么对应dfs的话这样：

bool find_dfs(int a, int b)
{
	visited[a]=true;
	for(int i=h[a];i!=-1;i=ne[i])
	{
		int j = e[i]
		if(j==b) return true
		if(!visited[j]) return find(j,b)
	}
	return false;
}

那么Python的话由于不太支持这种写法，那么就这样写：

def find_dfs(a,b):
    visited[a]=True
    i = h[a]
    while(i!=-1):
        j = e[i]
        if (j == b):
            return True
        if(not visited[j]):
            return find_dfs(j,b)
        i = ne[i]
    return False

这样的话就可以了，同样的，我们的这个用BFS的话，也简单

bool visited[N]
queue<int> q;
void find_bfs(int a,int b)
{
	q.push(a);
	visited[a]=true;
	while(q.size())
	{
		int t = q.front();
		if(t==b) return true;
		for(int i=h[t];i!=-1;i=ne[i])
		//遍历和当前这个节点直接相连接的点
		{
			int j = e[i];
			if(!visited[j])
			{
				visited[j] = true;
				q.push(j);
			}
		}
	}
	return false;
}

python的话也就是那个循环再改一下就好了。然后的话，这里我们python如果使用队列的话请使用这个：

import collections
q = collections.deque()

如果使用list的话，那么时间复杂度是O（n）。当然使用list然后搞个双指针去模拟队列的话那个也是O(1)。用法的话和list其实差不多，list主要是pop和insert这个操作的时间复杂度太高了。不想用这个的话，建议模拟队列。

路径搜索

okey，这里我们先进入第二个模块，就是咱们关于图的路径搜索。在这里我们将实现基本的路径搜索算法，以及对这些算法的一些优化，在什么时候使用这些算法都进行说明。同时对这些代码的模板进行一个说明，当然这些模板是需要记忆背诵的~这不仅仅针对算法竞赛，针对面试也是有帮助的。

那么我们先由简到难吧，我们先来两个比较简单的算法，也就是直接使用到咱们的领接矩阵去做的一个算法。也就是咱们的Floyd算法，还有朴素版本的DijKstra算法，分别针对多源最短路径和，单源最短路径。只得一提的是，咱们关于路径搜索的算法有5个算法，其中4个是单源最短路径算法，只有一个是多源的。所以可以发现在使用我们先介绍的Floyd算法和朴素版本的DijKstra的情况是比较“无助”的情况，也就是比较极端的情况。必须解决多源最短路径的时候只能上Floyd，当题目为稠密图，并且节点个数n的平方,和边的个数m相似的时候，最好的办法就只有朴素DijKstra算法了，其他的算法SPFA，Bellman-Ford,以及优化后的Dijkstra,算法的时间复杂度分别是O(m)(最坏O(m*n),O(m*n),O(mlogn)。但是同时他们最简单，那么我们开始吧。

多源最短路问题

OK，我们来到第一个版块，就是多源最短路的问题。

问题描述

那么首先的话我们需要知道什么是多源的最短路径，这个说白了就是给定一个图，然后这个图上有很多的节点，我们需要知道图上面任意两个点之间的一个最短距离。那么这个就是多源的一个最短路径问题。

Floyd实现模板

okey，我们在这里再看一下如何实现这个东西，原理的话简单描述一下其实就是这样的（这个部分的原理其实类似的）
假设一个图，有A，B，C，D四个节点，并且节点之间是连同的。这个时候想要知道A->B 的距离，那么我们会看一下如果中间经过C点的距离会不短一点，也就是说求得 distance[A][B] 和 distance[A][C]+distance[C][B] 之间有没有更短，之后假设有更短，更新一下，这个时候distance[A][B] 表示的就是经过了中转站C的时候A到B的距离，之后，我还不满足，于是我再查看一下在刚刚的基础上，我再经过中转D会不会更短一点，如果有在更新，如果更新了，那么distance[A][B] 表示的就是从A到B经过C，D中转之后的距离，同时也是最短的。

原理的话其实就是这样，非常的朴实无华的一个思想，因此实现也是非常的朴实无华，时间复杂度是N三次幂。

使用邻接矩阵的写法：
当然不能有负回路，可以有负的权边哈。

for(int k=1;k<=n;k++)
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			g[i][j] = min(g[i][k],g[k][j]);	
		}
	}
}

那么在这里比较难受就是，在存储距离的时候的话，我们还是要使用到这个二维表，原来存的是边，而且存的是相互相邻的边，所以没办法存多源的路径的时候还是要用到二维表，所以这个算法的话，没必要那啥。

单源最短路径问题

okey，我们接下来还有在这方面的三个算法，一个算法的优化，大概算是4个算法吧。那么这些算法解决的都是咱们的单源最短路的问题，也就是说以某一个节点出发，这个节点A到其他节点的最短路径的距离。虽然这边有大概4个算法，但是实际上需要掌握常用的算法其实就三个，两个很无奈的情况下的算法和一个比较通吃的算法。

Dijkstra算法

okey，我们先来简单朴素一点的算法。就是这个算法，算法原理其实是和咱们提到的多源最短路径的原理是类似的，只是说现在更新的只有一个点A。那么同样的我们假设我们使用的是邻接矩阵进行存储的一个东西，此时我们定义这几个东西：

int N = 10000;
bool st[N];
int dist[N];
int g[N][N];

dist 这个玩存储的意思是，1号点到其他点的最短距离。如果你要算的是2号点，那么你就初始化的时候先初始化2号点。
st[i] 表示1号点到i号点的最短距离已经确定了

朴素版本

那么这个的话，其实就是这个算法的核心，那么接下来就是编写代码了。

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra(int u)
{
    memset(dist, 0x3f, sizeof dist);
    //如果求2，那就dist[2]=0
    dist[1]=0;
    for(int i=0;i<n-1;i++)
    {
		int t = -1;
		//这一步是在dist数组当中找到没有确定最小距离的点当中，距离最小的节点。
		for(int j=1;j<=n;j++)
		{
			if(!st[j]&&(t==-1||dist[t]>dist[j])
			{
				t = j;
			}
		}
		//用t来对距离进行更新
		for(int j=1;j<=n;j++)
		{
			dist[j] = min(dist[j], dist[t] + g[t][j]);
		}
		st[t] = true;
	}
	if(dist[u] == 0x3f3f3f3f) return -1;
	return dist[u];
    
}

python的写法的话和这个大差不差，难受的就是python不支持这种循环，需要使用到while循环进行代替，但是看模板的话建议还是这个模板好看。

堆优化

之后的话，我们来到一个优化版本。这个优化的话其实非常简单，就是把那个在dist当中找没有被用过的最小的那个节点的时候进行一个优化，就是用小顶堆，把这个给优化了一下。我们直接看到代码。

typedef pair<int, int> PII;
int dist[N];     
bool st[N];     
int g[N][N];
// 求1号点到n号点的最短距离，如果不存在，则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    //0表示距离，1表示当前的节点，如果要2号节点那么就0,2
    heap.push({0, 1});  

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;

        if (st[ver]) continue;
        st[ver] = true;

        for (int j=1;j<=n;j++)
        {
            if (dist[j] > distance + g[ver][j])
            {
                dist[j] = distance + g[ver][j];
                heap.push({dist[j], j});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

邻接表

那么之后的话，咱们肯定还是要使用到咱们的邻接表去做一些存储，那么代码的话，其实改动不大，就是遍历的结构换一下。这个是我们堆优化版本的，那么朴素版本的修改也是一样的，只需要吧遍历节点的代码改成使用咱们给的这个数据结构的边即可。

typedef pair<int, int> PII;
int n;    
int h[N], w[N], e[N], ne[N], idx;      
int dist[N];     
bool st[N];     
// 求1号点到n号点的最短距离，如果不存在，则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    //0表示距离，1表示当前的节点，如果要2号节点那么就0,2
    heap.push({0, 1});  

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;

        if (st[ver]) continue;
        st[ver] = true;

        for (int i=h[ver];i!=-1;i++)
        {
        	int j = e[i];
            if (dist[j] > distance + w[i])
            {
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

那么关于这个时间复杂度的话，如果选择使用邻接表来的话，那么复杂度大概是： O(mlogn)。但是还是那个矩阵的话，那么那就是还是提升不大。所以如果要用堆优化的话，那么建议使用邻接表法，但是和接下来要提到算法来说，这个就low了，所以这个的话，记住朴素版本的Dijikstra算法就好了，这个你看着办，为什么的话，我们介绍完这个路径搜索的部分后，有个小结，我们到时候来简单分析一下。

python实现

那么之后的话是关于python的一个实现，首先朴素的实现我就不给了，因为这个python改一下循环就好了。那么就是优化之后的版本的话使用到了这个堆，那么这里的话我们也是使用实现好的，python标准库实现好了的headp来实现即可。

import heapq
def Djikstra_q(n:int):

    dist[1] = 0
    #定义一个用来存储的list
    heap = []
    #默认就是小顶堆
    heapq.heappush(heap,(0,1))
    while(len(heap)):
        t = heapq.heappop(heap)
        distance,ver = t[0],t[1]
        if(st[ver]):
            continue
        st[ver] = True
        i = h[ver]
        while(i!=-1):
            j = e[i]
            if(dist[j]>dist[ver]+w[i]):
                dist[j] = dist[ver]+w[i]
                if(not st[j]):
                      heapq.heappush(heap,(dist[j],j))
            i = ne[i]

    if (dist[n] == float("inf")):
        return -1
    return dist[n]

Bellman-Ford 算法

接下来就是这个，刚刚我们提到的Dijkstra算法呢，针对的是正权边，但是在针对负的权边的时候，就用不了了，那么这个是时候的话，这个算法就出来了，而且这个算法的实现其实非常简单，同时它的时间复杂度在O(mn)，并且它是有特殊含义的，在针对带有约束问题的时候，这个算法可能是唯一的解。

它的原理话非常直接，就是直接遍历全部的边，然后找到最短的边就好了。

实现

int n, m;     
int dist[N];    

struct Edge    
{
    int a, b, w;
}edges[M];

// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;


    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            if (dist[b] > dist[a] + w)
                dist[b] = dist[a] + w;
        }
    }

    if (dist[n] >= 0x3f3f3f3f / 2) return -1;
    return dist[n];
}

用这个算法的话，我们可以直接使用结构体来进行存储，同时这个算法第一个for循环的含义是，最多经过n个点，它的dist可以得到的最短距离。同时用这个算法可以用来判断是否存在负权回路。判断原理就是多循环一次，如果多循环一次之后dist[n]的值有变小，说明存在。
原因的话因为这个for循环的含义，他表示的是最多经过n个点进行中转之后的最短距离，如果存在负的回路的话，再走一次中转，那么肯定会变小。

SPFA 算法

OK，那么接下来的话，就到了咱们基本上可以通杀的算法了，每次就是这个算法，这个算法的话基本上都能用，如果有限制，中转的点不能超过K个，那么没办法就用Bellman,但是如果没有限制，那么的话可以直接先考虑这个算法，如果这个算法过不了，那么有可能是因为他是个稠密图，并且n~m^2 去了，那么这个时候那就只能走朴素版本的Djikstra算法了。因为它的时间复杂度是O(m) 最糟糕是 nm.

那么之后的话是这个算法的实现，这个算法的话其实和堆优化的算法有点相似，但原理的话是在Bellman的基础上进行改进，用队列进行优化，因为有些点存在重复计算的问题。

实现

OK，我们来直接看到实现。同样的我们这里采用邻接表来进行实现。那么既然使用到了这个，那么我们必不可少的是需要几个辅助的数组。
这里的话这个st数组的含义要变一下，其他的一样。

int n;    
int h[N], w[N], e[N], ne[N], idx;      
int dist[N];    
bool st[N];// 存储每个点是否在队列中

// 求1号点到n号点的最短路距离，如果从1号点无法走到n号点则返回-1
int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    queue<int> q;
    q.push(1);
    st[1] = true;
    while(q.size())
    {
 		auto t = q.front();
        q.pop();
        st[t] = false;
        for(int i = h[t];i!=-1;i=ne[i])
        {
        	int j = e[i];
			if(dist[j]>dist[t]+w[i])
			{
				dist[j] = dist[t]+w[i];
				if(!st[j])
				{
					q.push(j);
				    st[j] = true;
				}
			}
		}
	}
	if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

python 版本

之后的话又到了，万人瞩目的Python版本的实现，那么在这里的话，就是说咱们要使用到collections当中的这个队列就好了。

import collections
q = collections.deque()
def spfa():

    #1号节点开始
    q.append(1)
    st[1] = True
    while(len(q)):
        t = q.pop()
        st[t] = False

        i = h[t]
        while(i!=-1):
            j = e[i]
            if(dist[j]>dist[t]+w[i]):
                dist[j] = dist[t] + w[i]
                if(not st[j]):
                    q.append(j)
                    st[j]=True
            i = ne[i]
        if (dist[n] == float("inf")):
            return -1
        return dist[n]

其他的含义是一样的，动都没得。

判断负环

之后的话，我们这个spfa,算法还有一个非常光荣的任务，就是判断当前的这个图当中是不是存在负的环（当然题目当中如果可以直接使用到这些算法当然是不存在的，但是有些题目或者需求，可能就是需要你去判断一下图当中有没有负的环，那么的话就是需要使用到这个算法了）

这里的话也是使用到了抽屉原理进行一个判断，但是无所谓，我们只要把这个代码稍微改动一下就好了。

int n; 
int h[N], w[N], e[N], ne[N], idx;  
int dist[N], cnt[N]; //cnt[x]存储1到x的最短路中经过的点数    
bool st[N];   
// 如果存在负环，则返回true，否则返回false。
bool spfa()
{
    queue<int> q;
    for (int i = 1; i <= n; i ++ )
    {
        q.push(i);
        st[i] = true;
    }

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;  
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

同样的如果你想要搞Python版本的话，改一下就好了，改动不是特别大。

小结

okey，这里的话介绍了几个这方面的算法，那么上半部分算是结束了。那么现在的话我们来稍微小结一下这部分的内容。那么这里的话我们大概的话其实是有5个算法在这里，并且针对了两大类问题。一个是单源的最短路径问题，然后是多源的最短路径问题。大概就是这样的导图：

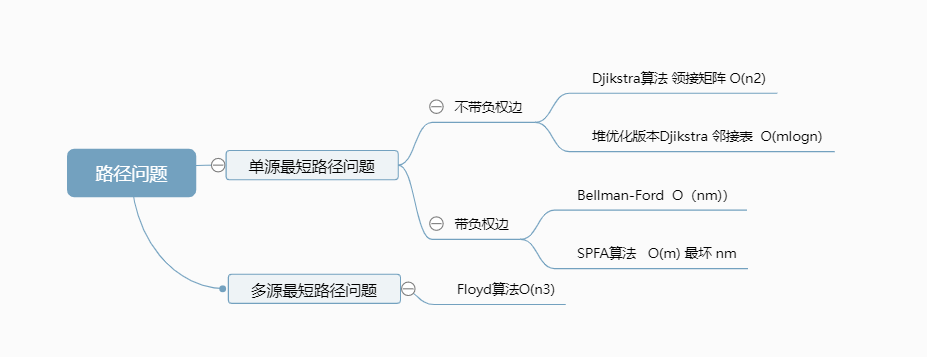
然后结合他们的特点，基本上，如果spfa解决不了，那么说明被卡了，那这个时候尝试Djikstra.如果是有其他要求，那么结合上面的正对问题，再去使用特定算法。

最小生成树

okey, 那么接下来我们进入另一个关于图的版块。那就是最小生成树。

一个连通图可以有多个生成树；
一个连通图的所有生成树都包含相同的顶点个数和边数； 生成树当中不存在环；
移除生成树中的任意一条边都会导致图的不连通， 生成树的边最少特性；
在生成树中添加一条边会构成环。
对于包含n个顶点的连通图，生成树包含n个顶点和n-1条边；
对于包含n个顶点的无向完全图最多包含 颗生成树。

说人话就是，找到一个图当中，能够连通，并且距离最小的路径。当然我们这边这个时候，从1号节点出发就可以了。

同样的，我们这里面其实也是有两种算法，一个是适用于稠密图的Prim算法，还有就是适用于稀疏图的Kruskal算法。

这两个算法的话比较简单，也是比较经典的算法。

Prim算法

这个算法的原理和Djikstra算法代码的实现其实很像。
当然这里的话是找点，给定一个图，我先选择一个点，加入到咱们的生成树当中，然后，找到第二个点，离我们的生成树距离最近的点，然后加入到我们的集合，直到我们把这个全部的点都加入到了生成树当中。

int n;      // n表示点数
int g[N][N];      
int dist[N];        // 存储其他点到当前最小生成树的距离
bool st[N];     // 存储每个点是否已经在生成树中

int prim()
{
	//统计距离
	int res = 0;
	memset(dist, 0x3f, sizeof dist);
	for(int i=0;i<n;i++)
	{
		int t = -1;
		//找到不在生成树当中的点，距离咱们生成树距离最短的点
		for(int j=1;j<=n;j++)
		{
			if(!st[j] && (t==-1||dist[t]>dist[j])
			{
				t = j;
			}
		}
		
		if (i && dist[t] == INF) return INF; //此时说明不是连通的图
		//找到了这个点，我们开始加入边,第一个点不是边，而且第一个点的编号其实就是1
		if(i)
		{
			//这个t就是我们选择的节点
			res+=dist[t];
		}
		//之后更新一下，其他点到生成树的距离
		for(int j=1;j<=n;j++)
		{
			dist[j] = min(dist[j],g[t][j]);
		}
	}

}

同样的，由于这个，我们发现就是找这个t时候时间复杂度比较高，那么这个时候我们也可以使用堆进行优化，但是堆优化的问题在于，如果想要达到合适的时间复杂度的话，需要考虑到使用邻接表，那么问题来了，使用邻接表的话我们有别的算法，就是这个Kruskra算法。时间复杂度也类似，当然这个Krushra 的时间复杂度主要集中在这个排序当中。

Kruskra算法

OK，我们来看看这个算法，这个算法的话核心，很简单，就是把所有的边进行排序，然后排序完毕之后的话，我们按照这个边进行组装成树就好了。并且我们使用到并查集进行一个合并，这里的时间复杂可以达到O（1）。

这里的话，我们会给出Python版本的一个模板。

实现

OK，我们先来看到这个是大概怎么做的，需要那些东西。

int n, m;       // n是点数，m是边数
int p[N];       // 并查集的父节点数组

struct Edge     
{
    int a, b, w;

    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)    
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

首先的话，我们就是需要这个，然后这个Edge是我们的一个边，并且写了一个可比较的玩意。

int kruskal()
{
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b)     // 如果两个连通块不连通，则将这两个连通块合并
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF;
    return res;
}

这部分的代码就非常的清晰了，当然这个cnt是指加入的边，按照我们的性质就是，最后的边的个数是n-1的，因为这样才能连通。

python版本

那么同样的，这个时候我们来看到这个Python版本的一个代码实现。这个Python版本的话更简单。
首先的话，我们同样是需要这个p数组的，因为我们需要使用到并查集嘛，当然Python的选择是非常多的，直接使用set来做也是可以的。没办法，不得不承认，Python有时候就是流氓。

首先的话，我们这样，同样我们存边，但是我们是这样的。我们的边直接用list存储。

edges = [(a,b,c)]

这个a,b 表示边，c表示边长

其实可以注意到，这个并查集在找到过程当中，实现了这个路径压缩的一个效果。

def find(a):
	if(p[a]!=a):
		p[a] = find(p[a])
	return p[a]

def Kruskal():
	 res = 0
	 cnt = 0
	 sorted(edgs,lambda x:x[2])
	 for i in range(1,n+1):
	 	p[i] = i
	 
	 for i in range(m):
	 	a,b,c = edges[i]
		#看看这两货有没合在一起，没有合在一起
	 	a = find(a)
	 	b = find(b)
	 	if(a!=b):
	 		p[a] = b; 
	 		res+=c
	 		cnt+=1
	 if(cnt<n-1):
	 	return float("inf")
	 		

二分图

之后的话就是二分图了，这个玩意是图里面比较抽象的东西，因为一般情况下都是抽象建模成一个二分图来做的。然后这一类题目比较灵活。

二分图性质

首先我们来看到什么是二分图。
形如这样的图：

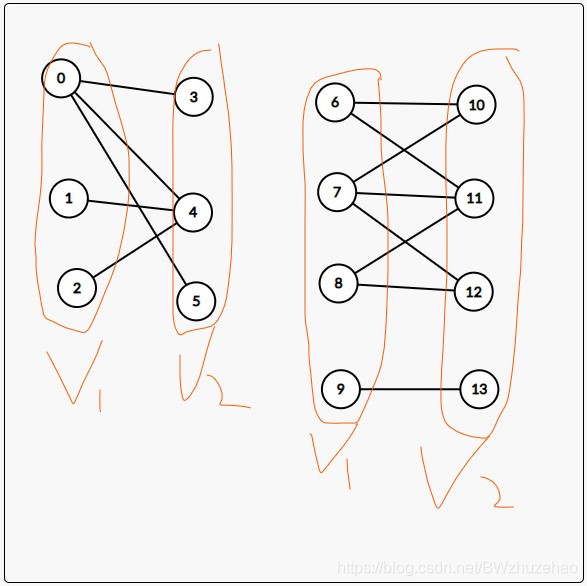
就叫做二分图，并且是无向的，这个图有什么特点呢，第一在图中，我们发点集能分成两个独立的点集。那么这个的话其实就是一个二分图，然后的话，他的重要的充要条件就是：无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。
同时这里注意的是：需要注意的是，二分图不一定要连通，比如上面的右边这张图，并不连通，但是其仍然是一张二分图

反正大概的话，一个二分图大概是长这样的。那么我们在这里需要做的有两个点，第一个是解决如何判断这个图是一个二分图，之后第二个点，是解决知道了这个是二分图的情况下，找出这个二分图的最大匹配。那么第二点的话，我们待会再说，我们先来看到如何去判断一个图是不是二分图。

染色法

原理

OK，我们先来解决第一个问题，就是这个如何判断是不是一个二分图，这里比较常用的做法就是使用染色法来进行一个判断，判断这个图是不是二分图。因为我们知道我们的这个图有一个性质，就是说可以把全部点分成两个不同的集合。就如上面那张图，所以这个时候，我们可以这样把左边的染成黑色，右边的染成白色。换一句话说，如果一个图，我可以把他们进行染色，并且可以用两种颜色就进行划分，那么这个图的话就是一个二分图。

并且我们拿到这个图为例：

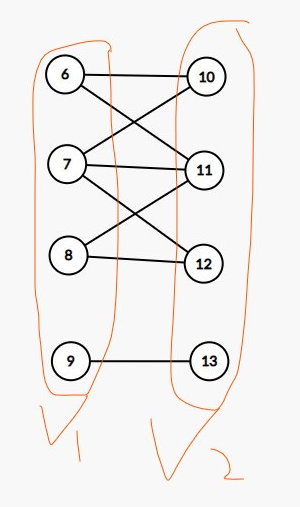
我们发现就是说，6号点和10,11号点相连，同时我们染色的话， 6,10,11号当中，6号点的演示是不同于10,11号的。并且观察其他的点，我们发现一个规律就是，如果要上色的话，我们把这个点和他直接相连接的点进行染色成相反的颜色就可以了。那么染色法的话，大概就是基于这个原理来的。

实现

然后我们直接看到实现，同样的，这里的话，我们是存入这个边，也就是用那个来做的，当然在这个版块的话，你用啥其实都可以，你怎么舒服怎么来，但是算法的模板要记住，知道它的一个含义就好。
首先我们还是老三样，我们用邻接表法。

int n;    
int h[N], e[M], ne[M], idx;     
int color[N];  //给当前节点上色，-1表示没有上色，0表示白色，1表示黑色。初始化的时候全部为-1
bool upcolor(int a,int c)
{
	//对当前点进行染色
	color[a] = c;
	for(int i=h[a];i!=-1;i=ne[i])
	{
		//看看当前和这个点相连的点有没有被染色，如果没有
		//染上相反的颜色，看看能不能染，不能染说明不行
		int j = e[i]
		if(color[j]==-1)
		{
			if(!upcolor(j,!c))return false;
			//可以染，但是颜色和当前的点一样说明有冲突也不行
			else if (color[j] == c) return false;
		}
	}
	return true;
}

bool check()
{
	for(int j=1;j<=n;j++)
	{
		//看看当前点有没有被染色，没有就去染色
		if(color[j]==-1)
		{
			if(!upcolor(j,0))
			{
				return false;
			}
		}
	}
	return true;
}

那么这个代码的话转化为python代码也比较简单，那么这个的话就不给出python代码了。

例题

https://leetcode-cn.com/problems/possible-bipartition
之后的话我们还是来看到相关的题目来，比较好理解，这个题目的话也很简单，直接套用这个模板就可以做了。

给定一组 N 人（编号为 1, 2, …, N）， 我们想把每个人分进任意大小的两组。

每个人都可能不喜欢其他人，那么他们不应该属于同一组。

形式上，如果 dislikes[i] = [a, b]，表示不允许将编号为 a 和 b 的人归入同一组。

当可以用这种方法将每个人分进两组时，返回 true；否则返回 false。

示例 1：
输入：N = 4, dislikes = [[1,2],[1,3],[2,4]]
输出：true
解释：group1 [1,4], group2 [2,3]

示例 2：
输入：N = 3, dislikes = [[1,2],[1,3],[2,3]]
输出：false

示例 3：
输入：N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
输出：false

这个题目的话，乍一看应该是比较抽象的（题解的话，这个我就不写了，套模板即可，文章篇幅太长了，顺便带点思考看本文~，绝对不是因为博主偷懒！！！）

okey，我们直接来看吧，首先的话，我们的二分图有个特点，就是说，可以把点分为两个集合u,v,并且在不同的集合当中，是没有直接相连的点的，对吧。那么如果我们划分人，去分组，那么分好组之后，是不是每个分组之间的人，都是不讨厌的，如果我们把讨厌关系看做是边，那么如果我们把 a,b两个人看做节点，相互讨厌看做是一条边，那么这不是建立了一个图吗。我只需要这个图是不是二分图不就完了吗。

okey，这个就是思路。

匈牙利算法

嗯，这个算法算是老朋友，大一数据建模的时候就学习到了这个算法，时间飞逝，一眨眼我就变成老油条了，咳。那么这个东西，在图当中，在这个二分图当中解决的是什么问题呢，就是匹配问题。那么我们先来看一下什么是匹配问题。

匹配

这个的话直接看到我们待会对应匈牙利算法的一个解释的时候也可以，这样的话会更明朗一点儿。
我们先来看到这个例子吧：
指在当前已完成的匹配下无法再通过增加未完成匹配的边的方式来增加匹配的边数
给定一个二分图G(X,E,Y)，F为边集E的一个子集。如果F中任意两条边都没有公共端点，则称F是图G的一个匹配。

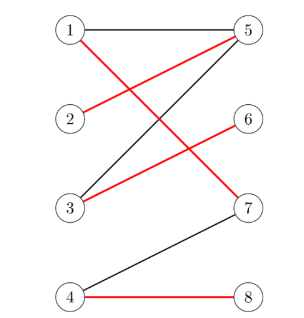
极大匹配(Maximal Matching)是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。
如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。
求二分图最大匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm)。

算法原理

首先明确一点，就是我们用这个算法的时候，条件是我们已经知道了这个图，或者说我们构建的这个图是一个二分图。这个是前提，然后再去做匹配。并且在做匹配之前，已经有了一些连接，或者说是前置条件。什么是已有连接呢，这个我们待会解释。

我们先拿一个案例来介绍这个匈牙利算法。这个匈牙利算法呢，又可以叫做“相亲算法”，“找老婆算法”。当然这个是戏称，因为有一个非常经典的案例，就是这个给定这样的一个任务：叫你当月老（财神爷）。

现在有这样一群男女嘉宾：

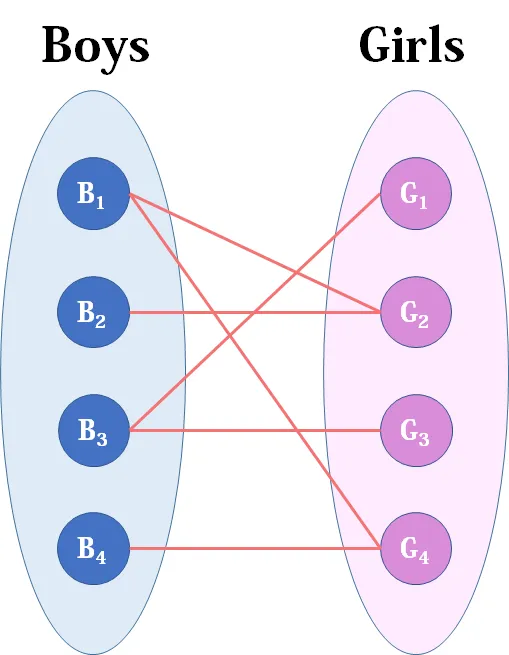
然后捏，现在呢，我们通过一段时间的认识，有一些男女嘉宾互相看上了眼，这些连线就表示，嘉宾之间看上了眼。例如：B1,连接G2,G4。就是说，男一号看上了女2,4号。同样的看女二号，她和B1，B2连接了，也就是，女二号也看上了男1号和2号。此时你是月老，或者说你是相亲大会的主持人。你现在需要根据这个情况，去给这些男女去配对。争取让每一个男的都可以和对话心仪的女孩子配对。之所以需要我们安排配对呢原因很简单，因为有个别女的或者男滴，同时看上了好几对象，然后有些男滴A可能只是看上了一个对象，并且那个女的B已经配对上了一个男滴C，但是那个男滴C是吾辈楷模，他还有个备胎，并且愿意和备胎搞，那么这个时候女B就可以空闲出来了（当然那个女的B也是看上了,同时也看上了C，只是先和C配对了）所以这样的话，就给我们操作空间了。没办法双方的备胎都挺多的，给那些看起来稍微“老实一点人”机会。当然这个只是一个例子，请勿对号入座！

那么我们的这算法就是完成这个任务，那么如何完成呢，其实很简单，就是咱们刚刚说的。来举个例子：现在A看上了B,C这两个女嘉宾。现在假设我们让A和B进行配对。之后我们对D这个男嘉宾进行配对，假设男嘉宾D，他只看上了女嘉宾B，（女嘉宾同时看上了男嘉宾A,D，现在和男嘉宾A进行配对中）。这个时候就会去找到男嘉宾A，发现男嘉宾A还看上了女嘉宾K，并且愿意和K再配对。那么这个时候我们就让A和K配对，然后把D和B配对。但是如果男嘉宾A也只看上了B，那么没办法谁让人家先来呢，那么这个时候真没法配对了，就算了。

OK，这个的话就是我们的一个流程，那么代码的话其实也很好写，难的是怎么用。

实现

现在我们假设，我们已经准备好了两个集合，也就是说一个图，我们已经划分好了，或者说这个二分图我们已经搭建好了哈。

现在继续我们当相亲大赛主持人的身份。

int n1, n2;     // 男女嘉宾的编号
int h[N], e[M], ne[M], idx;    
int match[N];       // 女嘉宾和那个男滴在配对
bool st[N];     // 女嘉宾有没有最终确定配对
bool find(int a)
{
	//男嘉宾a上场
	for(int i=h[a];i!=-1;i=ne[i])
	{
		//查看男嘉宾看上的女嘉宾有没有配对
		int j = e[i];
		//没有配对，我们去配对
		if(!st[j])
		{
			st[j] = true;
			if(match[j]==0||find(match[j])
			{
				//如果match=0此时这个女嘉宾还没有匹配，那么此时双方匹配
				//如果已经配对了，那么看看和当前女嘉宾配对的男嘉宾能不能再配对
				match[j] = a;
				return true;
			}
		}
	}
	return false;

}

那么这个的话就是我们寻找配对的过程，当然我们现在只是给一个男嘉宾a进行了配对，我们接下来需要对所有的男嘉宾进行配对：

int res = 0; //配对了多少个
for (int i = 1; i <= n1; i ++ )
{
    memset(st, false, sizeof st);//每次都需要清空st数组，因为匹配好的一对可能会有下家
    if (find(i)) res ++ ;
}

当然这些都是很灵活的，不一样的是邻接表来写也是可以的。口诀的就是：

1. 来两个东西，记录匹配的边和记录一个东西也没有确定被匹配
2. 拿过来一个节点，看一看能够和这个节点匹配的节点。然后按照咱们的“相亲”规则进行判断
3. 全部“男嘉宾”进行处理，也就是另一半集合。

案例

我们来一个实际的题目吧：
https://ac.nowcoder.com/acm/contest/1062/B

给定一个N行N列的棋盘，已知某些格子禁止放置。求最多能往棋盘上放多少块的长度为2、宽度为1的骨牌。骨牌的边界与格线重合(骨牌占用两个格子),并且任意两张骨牌都不重叠。N,M≤100。

第一行为n，m（表示有m个删除的格子）
第二行到m+1行为x,y，分别表示删除格子所在的位置
x为第x行
y为第y列

输入
8 0

输出
32

题目大概就是这个样子。

提示是用二分图去做，并且解压转换为最大匹配问题，然后使用到匈牙利算法去解决这个问题。

二分图匹配的模型有两个要素：

1.节点能分成两个独立的集合，每个集合内部没有边互相连接。

2.每一个节点只能与另一个集合有一条匹配边相连

那么我们仔细看到题目的描述，描述怎么说的，在里面，有一个任意两张骨牌都不重叠，并且一个骨牌，占了两个小格子。好，第一个问题，如果重合了会发生什么明显的现象，因为骨牌占了两个格子，我们假设骨牌有头部和尾部组成，头部和尾部各占一个格子。那么如果这两个重合了，那么必然就是存在两个骨牌或者多个骨牌，他们的头部和头部重合了，或者头部和尾部重合了。那么如果要避免重合，那么首先就要保证，所有骨牌的头部和尾部在棋盘上面对应的小格子不能有重复。也就是说对应骨牌头部的格子和对于骨牌尾部的格子，不能在同一个集合，那么这里恰好划分了两个集合出来。并且两个集合当中的格子，通过同一块骨牌可以连起来。

OK，这个时候，好像已经符合了二分图的特点。那么问题来了，如何保证这个集合不会重复，或者说，我隐约感觉到了可以这样做，但是怎么做，这个二分图如何建立。

骨牌不能对角线放置对吧，并且我们的头部和尾部不能在同一个集合，要分开。所以对角线上面不可能出现头部和尾部，同时又要能够区分头部和尾部，那么既然如此，那么如果我按照对角线交叉放置头部和尾部的话，不就刚好可以把这两个家伙分开了么。

于是如下图进行放置：

我们把蓝色看成是男嘉宾，白色点看成是女嘉宾。然后题目问的是最多可以放置多少个骨牌，那么此时不就相当于，男女嘉宾可以匹配多少对了么。

这个案例的建模过程很抽象。

那么接下来就是实现：

#include<iostream>
#include<cstring>
using namespace std;
int res;
typedef pair<int, int>PII;
const int N = 1e3;
int n, t;
bool g[N][N];
bool st[N][N];
PII match[N][N];
int dx[]={1,-1,0,0},dy[]={0,0,-1,1};
bool find(int x,int y)
{
	//找到当前男嘉宾可以匹配的女嘉宾
    for(int i=0;i<4;i++)
    {
        int a=x+dx[i];
        int b=y+dy[i];
        if(st[a][b])
        {continue;}
        if(g[a][b])
        {
            continue;
        }
        if(a<=0 || a>n || b<=0 || b>n)
        {
            continue;
        }
        st[a][b]=true;
        if(match[a][b].first==0 || find(match[a][b].first,match[a][b].second))
        {
            match[a][b]={x,y};
            return true;
        }
    }
    return false;
}
int main()
{
    cin>>n>>t;
    for(int i=0;i<t;i++)
    {
        int a,b;
        cin>>a>>b;
        g[a][b]=true;
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if((i+j)%2==0 && !g[i][j])
            {
            	// 和为偶数当做男嘉宾
                memset(st,false,sizeof st);
                if(find(i,j))
                {
                    res++;
                }
            }
        }
    }
    cout<<res<<endl;
}

最后的话还有一点就是关于初始化的时候，C++是有这个memset来快速完成这个初始化的，那么Python的话其实可以直接使用[0]*m 这种方式进行初始化，或者列表表达式，推荐前者。但是如果你是[[],[]]这种结构的话，使用表达式，因为前者是引用会出问题的。

总结

okey，恭喜你，看到了结尾~