一个正整数 n
可以表示成若干个正整数之和，形如：n=n1+n2+…+nk
，其中 n1≥n2≥…≥nk,k≥1
。

我们将这样的一种表示称为正整数 n
的一种划分。

现在给定一个正整数 n
，请你求出 n
共有多少种不同的划分方法。

输入格式
共一行，包含一个整数 n
。

输出格式
共一行，包含一个整数，表示总划分数量。

由于答案可能很大，输出结果请对 109+7
取模。

数据范围
1≤n≤1000
输入样例:
5
输出样例：
7

思考问题没有思路的时候，考虑先找一个简单的数列一下，演算一下。

（1）背包做法
容量为n的背包，物品n个1-n，每个物品可以用无限次，也就是完全背包问题。
集合表示为：从1 - i个物品中选出体积恰好是j的方案数


替换一下：

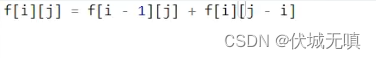
优化掉一维，体积从大到小循环。

#include <iostream>
#include <algorithm>

const int MOD = 1e9 + 7, N = 1010;

int n;
int f[N];

int main ()
{
    scanf("%d", &n);
    f[0] = 1;
    
    for(int i = 1; i <= n; i ++ )
        for(int j = i; j <= n; j ++ )
            f[j] = (f[j] + f[j - i]) % MOD;
    
    printf("%d\n", f[n]);
    
    return 0;
}

（2）另一种状态转移方程的做法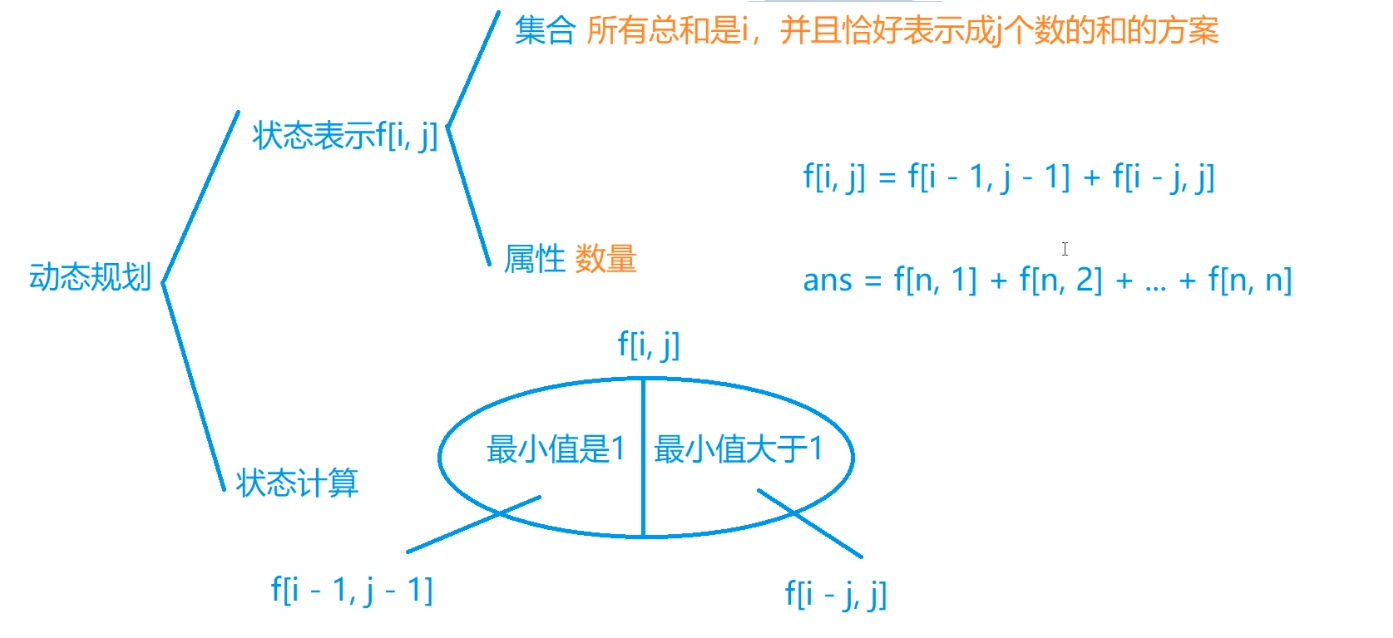

// #include <iostream>
// #include <algorithm>

// const int MOD = 1e9 + 7, N = 1010;

// int n;
// int f[N];

// int main ()
// {
//     scanf("%d", &n);
//     f[0] = 1;
    
//     for(int i = 1; i <= n; i ++ )
//         for(int j = i; j <= n; j ++ )
//             f[j] = (f[j] + f[j - i]) % MOD;
    
//     printf("%d\n", f[n]);
    
//     return 0;
// }

#include <iostream>
#include <algorithm>

const int MOD = 1e9 + 7, N = 1010;

int n;
int f[N][N];

int main ()
{
    scanf("%d", &n);
    
    f[0][0] = 1;
    
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= i; j ++ )
            f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % MOD;
    
    int res = 0;
    for(int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % MOD;
    
    printf("%d\n", res);
    
    return 0;
}