1129. 热浪(活动 - AcWing)

思路:题目只是加了一个背景,但实际上还是很裸的单源最短路问题。我们有四种写法,bellman_ford算法时间复杂度不如spfa,而且这里对边数没有限定,所以没必要使用bellman_ford。然后我们就时间复杂度进行分析,朴素版dijkstra算法的时间复杂度是O(n^2),本题的点数是2500,n^2=6250000,数量级1e6,可以过;堆优化的dijkstra,时间复杂度O(mkogn),6200log2500=21067(约等),数量级是1e4,也是可以过的;spfa一般时间复杂度是O(m),m=6200,数量级是1e3,最坏O(nm)=15500000,数量级是1e7,也没问题。那么我们本着复习算法将所有的都写一下。
朴素版dijsktra:
#include<bits/stdc++.h>
using namespace std;
const int N=3000,M=7000;
int n,m;
int s,e;
int g[N][N];
int d[N],st[N];
int dijkstra()
{
memset(d,0x3f,sizeof d);
d[s]=0;
for(int i=1;i<=n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j]&&(t==-1||d[t]>d[j])) t=j;
st[t]=1;
for(int i=1;i<=n;i++)
if(g[t][i]!=0x3f3f3f3f)
d[i]=min(d[i],d[t]+g[t][i]);
}
if(d[e]!=0x3f3f3f3f) return d[e];
else return -1;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&e);
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b]=g[b][a]=min(g[a][b],c);
}
cout<<dijkstra();
}堆优化版dijkstra
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=3000,M=7000*2;
int h[N],e[M],ne[M],w[M],idx;
int st[N],d[N];
int n,m,ts,te;
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dijkstra()
{
memset(d,0x3f,sizeof d);
d[ts]=0;
priority_queue<pii,vector<pii>,greater<pii>>q;
q.push({0,ts});
while(q.size())
{
auto t=q.top();
q.pop();
int dist=t.first,v=t.second;
if(st[v]) continue;
st[v]=1;
for(int i=h[v];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>d[v]+w[i])
{
d[j]=d[v]+w[i];
q.push({d[j],j});
}
}
}
if(d[te]!=0x3f3f3f3f) return d[te];
else return -1;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&ts,&te);
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
cout<<dijkstra();
}spfa
#include<bits/stdc++.h>
using namespace std;
const int N=3000,M=7000*2;
int n,m,ts,te;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N];
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int spfa()
{
queue<int>q;
memset(d,0x3f,sizeof d);
d[ts]=0;
q.push(ts);
while(q.size())
{
auto t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>d[t]+w[i])
{
d[j]=d[t]+w[i];
if(!st[j])
{
st[j]=1,q.push(j);
}
}
}
}
if(d[te]!=0x3f3f3f3f) return d[te];
else return -1;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&ts,&te);
memset(h,-1,sizeof h);
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
cout<<spfa();
}1128. 信使(活动 - AcWing)

思路:这道题很容易想到bfs,相当于从一个点开始往外扩散,不过这题有边权,所以不能用bfs来求解。但是求的是所有哨所受到消息的最小时间,我们可以把每个哨所的最小时间求出来,然后求一个max。
然后就是考虑时间复杂度的问题,朴素版O(n^2)=1e4,堆优化O(mlogn)=400,spfa一般O(m)=200 最坏O(nm)=2e4,所以三种算法都可以,这里还是本着复习的想法全部写一遍。
朴素版dijkstra
#include<bits/stdc++.h>
using namespace std;
const int N=120;
int g[N][N],d[N],st[N];
int n,m;
int dijkstra()
{
memset(d,0x3f,sizeof d);
d[1]=0;
for(int c=0;c<n;c++)
{
int t=-1;
for(int i=1;i<=n;i++)
if(!st[i]&&(t==-1||d[t]>d[i]))t=i;
st[t]=1;
for(int i=1;i<=n;i++)
{
if(!st[i]&&d[i]>d[t]+g[t][i])
{
d[i]=d[t]+g[t][i];
}
}
}
int flag=1,mx=0;
for(int i=1;i<=n;i++)
{
if(d[i]==0x3f3f3f3f)
{
flag=0;
break;
}
mx=max(mx,d[i]);
}
if(flag) return mx;
else return -1;
}
int main()
{
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof g);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b]=g[b][a]=min(g[a][b],c);
}
cout<<dijkstra();
}堆优化版dijkstra
#include<bits/stdc++.h>
using namespace std;
const int N=110,M=410;
int h[N],e[M],ne[M],w[M],idx;
int n,m;
int d[N],st[N];
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
typedef pair<int,int> pii;
int dijkstra()
{
memset(d,0x3f,sizeof d);
d[1]=0;
priority_queue<pii,vector<pii>,greater<pii>>q;
q.push({0,1});
while(q.size())
{
auto t=q.top();
q.pop();
int dist=t.first,v=t.second;
if(st[v]) continue;
st[v]=1;
for(int i=h[v];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>dist+w[i])
{
d[j]=dist+w[i];
q.push({d[j],j});
}
}
}
int flag=1,mx=0;
for(int i=1;i<=n;i++)
{
if(d[i]==0x3f3f3f3f)
{
flag=0;
break;
}
mx=max(mx,d[i]);
}
if(flag) return mx;
else return -1;
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
cout<<dijkstra();
}spfa
#include<bits/stdc++.h>
using namespace std;
const int N=110,M=410;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N];
int n,m;
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int spfa()
{
memset(d,0x3f,sizeof d);
d[1]=0;
queue<int>q;
q.push(1);
while(q.size())
{
int t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>d[t]+w[i])
{
d[j]=d[t]+w[i];
if(!st[j])
{
q.push(j);
st[j]=1;
}
}
}
}
int flag=1,mx=0;
for(int i=1;i<=n;i++)
{
if(d[i]==0x3f3f3f3f)
{
flag=0;
break;
}
mx=max(mx,d[i]);
}
if(flag) return mx;
else return -1;
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
cout<<spfa();
}1127. 香甜的黄油(1127. 香甜的黄油 - AcWing题库)

思路:这题的题意翻译一下就是找一个点,从这个点其他所有点的距离和最小。我们来看,如果一个点到其他点的距离和最小,那么到每个点应该取最短距离,对于每个点我们都要这么求一下,然后取最小值。朴素版dijkstra的时间复杂度是O(n^2)=640000,再乘上p个点,那么就是2e8,2e8的时间复杂度或许能够卡过去,但是不保险;堆优化版O(mlogn)约为4209,再乘上p,差不多3e6,肯定可以过;spfa一般来说是O(m),最坏O(nm),那么时间复杂度就在1e6~9e8,实际上应该不会卡到2e8的时间复杂度,所以可以试试,不行就换堆优化版的dijkstra。这里我们把spfa和堆优化版dijkstra都写一下。
堆优化版dijkstra
#include<bits/stdc++.h>
using namespace std;
const int N=810,M=3010;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N];
int n,p,m;
int id[N];
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
typedef pair<int,int> pii;
int dijkstra(int s)
{
memset(d,0x3f,sizeof d);
memset(st,0,sizeof st);
d[s]=0;
priority_queue<pii,vector<pii>,greater<pii>>q;
q.push({0,s});
while(q.size())
{
auto t=q.top();
q.pop();
int v=t.second,dist=t.first;
if(st[v]) continue;
st[v]=1;
for(int i=h[v];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>dist+w[i])
{
d[j]=dist+w[i];
q.push({d[j],j});
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
int j=id[i];
if(d[j]==0x3f3f3f3f) return 0x3f3f3f3f;
ans += d[j];
}
return ans;
}
int main()
{
scanf("%d%d%d",&n,&p,&m);
for(int i=1;i<=n;i++) scanf("%d",&id[i]);
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
int res=0x3f3f3f3f;
for(int i=1;i<=p;i++) res=min(res,dijkstra(i));
cout<<res;
}spfa
#include<bits/stdc++.h>
using namespace std;
const int N=810,M=3010,inf=0x3f3f3f3f;
int n,p,m;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N],id[N];
void add(int a,int b,int c)
{
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int spfa(int s)
{
memset(d,0x3f,sizeof d);
d[s]=0;
queue<int>q;
q.push(s);
while(q.size())
{
int t=q.front();
q.pop();
st[t]=0;
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(d[j]>d[t]+w[i])
{
d[j]=d[t]+w[i];
if(!st[j])
{
st[j]=1;
q.push(j);
}
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
int j=id[i];
if(d[j]==inf) return inf;
ans += d[j];
}
return ans;
}
int main()
{
scanf("%d%d%d",&n,&p,&m);
for(int i=1;i<=n;i++) scanf("%d",&id[i]);
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
int res=inf;
for(int i=1;i<=p;i++)
{
res=min(res,spfa(i));
}
cout<<res;
}1126. 最小花费(活动 - AcWing)

这道题我们已知起点和终点,但是这里不再是加法,不过实际上还是求最小,那么就可以用最短路来考虑,有两种思路,
我们设起点金额是ds,中间经过一系列折损pi,ds*p1*p2*...*pn=de,de确定是100,ds尽可能的小,那么就要这一系列乘积尽可能的大。虽然这里是最大,但是我们存边可以存成实际的百分数,那么就会越乘越小,所以当一个位置第一被作为最大的挑出来的时候,就是此处最大的位置。
#include<bits/stdc++.h>
using namespace std;
int n,m,s,e;
double g[2010][2010];
int st[2010];
double d[2010];
double dijkstra()
{
d[s]=1;
for(int i=1;i<=n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
if(!st[j]&&(t==-1||d[t]<d[j])) t=j;
st[t]=1;
for(int j=1;j<=n;j++)
d[j]=max(d[j],d[t]*g[t][j]);
}
return 100/d[e];
}
int main()
{
scanf("%d%d",&n,&m);
memset(g,0,sizeof g);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
double z=(100.0-c)/100;
g[a][b]=g[b][a]=max(g[a][b],z);
}
scanf("%d%d",&s,&e);
double ans=dijkstra();
printf("%.8lf",ans);
}另外还有一个思路就是从B往前找,求出最小的A。这时候边权是大于1的,越乘越大,自然可以找到最小值。
#include<bits/stdc++.h>
using namespace std;
int n,m,s,e;
int g[2010][2010],st[2010];
double d[2010];
double dijkstra()
{
for(int i=1;i<=n;i++) d[i]=1e100;
d[e]=100.0;
for(int i=1;i<=n;i++)
{
int t=-1;
for(int j=1;j<=n;j++)
{
if(!st[j]&&(t==-1||d[j]<d[t])) t=j;
}
st[t]=1;
for(int j=1;j<=n;j++)
{
if(st[j]||g[t][j]==0x3f3f3f3f) continue;
double p=(100-g[t][j])/100.0;
d[j]=min(d[j],d[t]/p);
}
}
return d[s];
}
int main()
{
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof g);
for(int i=1;i<=m;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b]=g[b][a]=min(g[a][b],c);
}
scanf("%d%d",&s,&e);
double ans=dijkstra();
printf("%.8lf",ans);
}920. 最优乘车(920. 最优乘车 - AcWing题库)

这里要获得最少换乘次数,而且公交线路是单程的,看似很麻烦,我们可以这么来处理,我们计算出最少坐车次数,用这个减1就是最少换乘次数。那么这个坐车次数该怎么求呢,我们可以将同一线路中的点之间,按照车到站的顺序连一条边权为1的边。然后去搜到终点的最短路。
#include<bits/stdc++.h>
using namespace std;
int m,n;
int g[600][600];
int d[600];
int id[600];
void bfs()
{
memset(d,0x3f,sizeof d);
d[1]=0;
queue<int>q;
q.push(1);
while(q.size())
{
auto t=q.front();
q.pop();
for(int i=1;i<=n;i++)
if(g[t][i]&&d[i]>d[t]+1)
{
d[i]=d[t]+1;
q.push(i);
}
}
}
int main()
{
scanf("%d%d",&m,&n);
string s;
getline(cin,s);
while(m--)
{
getline(cin,s);
stringstream ss(s);
int cnt=0,p;
while(ss>>p) id[cnt++]=p;
for(int i=0;i<cnt;i++)
for(int j=i+1;j<cnt;j++)
g[id[i]][id[j]]=1;
}
bfs();
if(d[n]==0x3f3f3f3f) printf("NO");
else printf("%d",d[n]-1);
}903. 昂贵的聘礼(活动 - AcWing)



 思路:这题乍一看没什么头绪,但是每一个个物品我们有多种获取方式,这里可以联想到dp,由于情况太多,进一步联想到建图。我们先来分析样例,样例中等级没有什么限制那么就先不管。如果一个物品可以替换另一物品那么我们就建一条有向边。
思路:这题乍一看没什么头绪,但是每一个个物品我们有多种获取方式,这里可以联想到dp,由于情况太多,进一步联想到建图。我们先来分析样例,样例中等级没有什么限制那么就先不管。如果一个物品可以替换另一物品那么我们就建一条有向边。
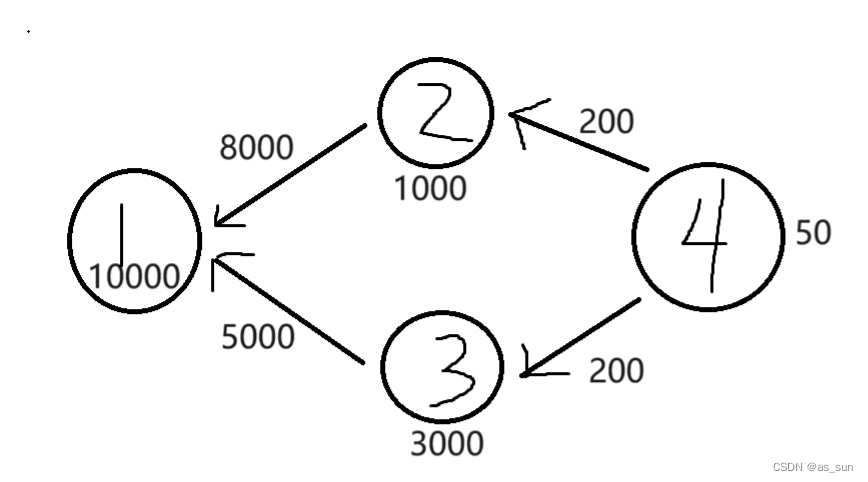
这样物品与物品之间的关系就很清楚了,但是这个图从什么地方开始循环还是不明朗的。而且用原价买这种方式应该也要建一条边,我们的图中并没有体现出来。那么我们可以假定一个虚拟原点。
那么很显然我们可以从虚拟原点出发,找到一个到1距离最短的路径。
然后就是等级问题,这里合法的对象肯定是在一个合法区间中间,也就是区间左右的等级差是m。另外还要注意一点,酋长的等级不一定最高,所以我们要把酋长作为左端点和作为右端点的情况都考虑到。这里N的范围是100以内,然后我们差不多要进行M次查找,所以这里可以用朴素版dijkstra,时间复杂度差不多是1e6。
#include<bits/stdc++.h>
using namespace std;
int p[120],level[120],g[120][120];
int m,n;
int d[120],st[120];
int dijkstra(int down,int up)
{
memset(d,0x3f,sizeof d);
memset(st,0,sizeof st);
d[0]=0;
for(int i=1;i<=n;i++)
{
int t=-1;
for(int j=0;j<=n;j++)
{
if(!st[j]&&(t==-1||d[t]>d[j])) t=j;
}
st[t]=1;
for(int j=1;j<=n;j++)
{
if(g[t][j]&&down<=level[j]&&level[j]<=up)
d[j]=min(d[j],d[t]+g[t][j]);
}
}
return d[1];
}
int main()
{
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++)
{
int c;
scanf("%d%d%d",&p[i],&level[i],&c);
g[0][i]=p[i];
for(int j=1;j<=c;j++)
{
int in,d;
scanf("%d%d",&in,&d);
g[in][i]=d;
}
}
int res=0x3f3f3f3f;
for(int i=level[1]-m;i<=level[1];i++) res=min(res,dijkstra(i,i+m));
cout<<res;
}