双端队列，优先队列，单调队列

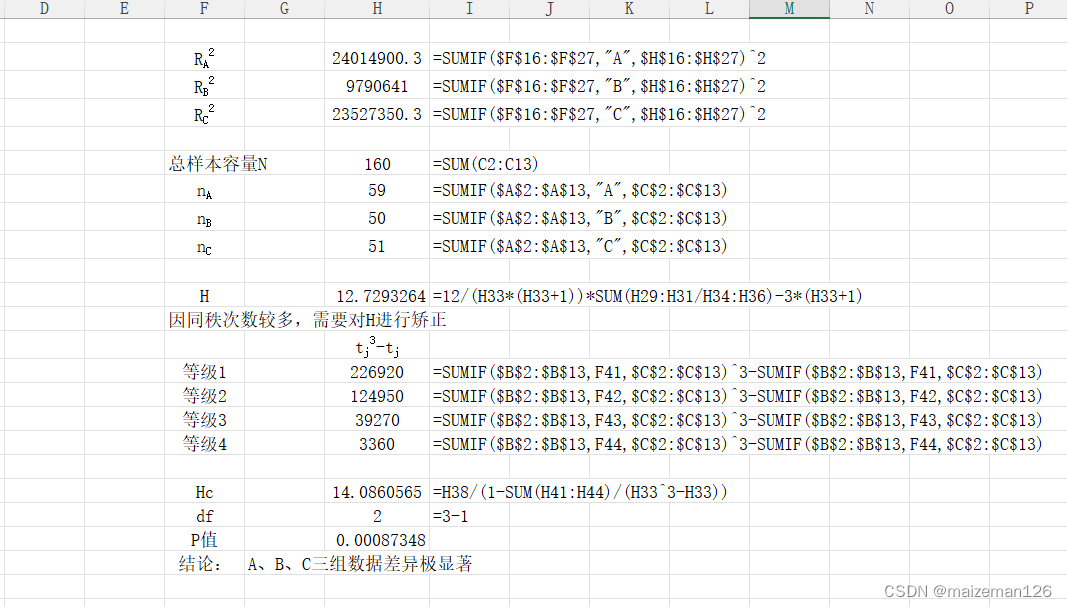
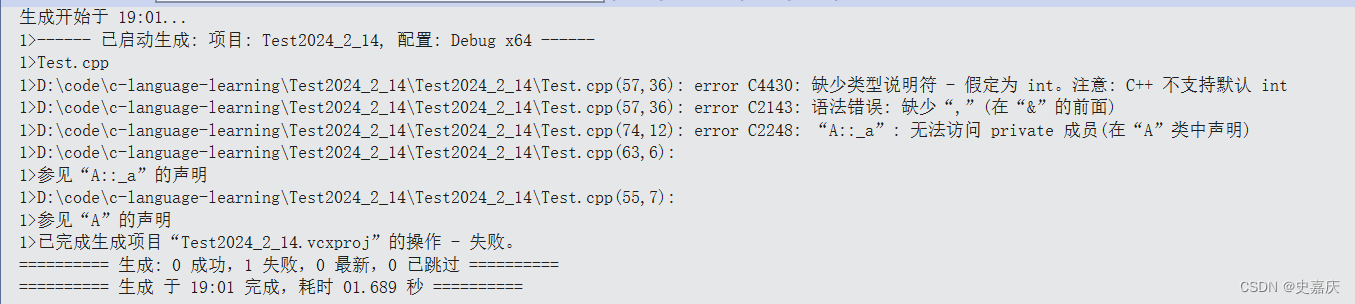
单调队列

单调队列是指一个队列内部元素具有单调性的数据结构

分为单调递增队列和单调递减队列

单调队列满足三个性质：

单调队列也是队列，满足先进先出
单调队列必须满足从队头到队尾的单调性
排在队列前面的元素比排在队列后面的元素要先进队

代码实现上的动作点：

维护队尾：保证单调性，及时排除不可能成为最优的决策。
维护队头：保证队内元素满足某种限制（比如区间的长度），确保决策集的合法性。

在这里插入图片描述

代码实现：

因为这是在头尾两端进行操作，所以用双端队列

class monoQueue{
    /*单调递减队列*/
public:
    // 在队尾添加元素
    void push(int val);
    // 队头元素如果是val，删除它
    void pop(int n);
     // 返回当前队列中的最大值--队头
    int max(){
        return dq.front();
    }
      //遍历元素
    void traverse(){
        for (int i = 0; i < dq.size();i++){
            cout << dq[i] << " ";//别忘了双端队列的下标访问
        }
        cout << endl;
    }
private:
    deque<int> dq;
};
void monoQueue::push(int val){
    //入队前，把小于x的元素出队
    while(!dq.empty()&& dq.back()<val){
        dq.pop_back();
    }
    dq.push_back(val);
}
void monoQueue::pop(int val){
    //判断队头元素,一定要判断队头存在性
    if(!dq.empty() && dq.front()==val){
        dq.pop_front();
    }
}

双端队列使用

push_front(val),pop_front()
push_back(val),pop_back()

#include<iostream>
#include<deque>//双端队列头文件
using namespace std;
int main(){
    deque<int> deq = {1, 2, 3};//初始化
    deq.push_front(11);
    deq.push_front(22);
    deq.push_back(33);
    deq.push_back(44);
    for(auto v:deq)
        cout << v << " ";//22 11 (1 2 3) 33 44
    deq.pop_front();
    deq.pop_back();
    cout << endl;
    for(auto v:deq)
        cout << v << " ";// 11 (1 2 3) 33 
     return 0;
}

可以用名称加下标对双端队列进行访问

deque<int> deq = {1, 2, 3};//初始化
    deq.push_front(11);
    deq.push_front(22);
    deq.push_back(33);
    deq.push_back(44);
    for (int i = 0; i < deq.size();i++)
        cout << deq[i] << " ";

deque存储特殊类型的元素

 struct student{
        int age;
        string name;
        student(int a,string b):age(a),name(b){}
    };
    deque<student> deq;
    student a(15, "daming");
    student b(20, "amy");
    student c(30, "alice");
    student d(33, "mary");
    deq.push_front(a);
    deq.push_back(b);
    deq.push_front(c);
    deq.push_back(d);
    for(auto [k,v]:deq){
        cout << k << "," << v << endl;
   }

30,alice
15,daming
20,amy
33,mary

迭代器

begin(),end() vs cbegin(),cend()-----区别就是c是const，不可修改值

deque<char> deq = {'a', 'b', 'c', 'd', 'e'};
     for (auto it = deq.begin(); it != deq.end();it++)
         (*it) += 1;
     for (auto it = deq.cbegin(); it != deq.cend(); it++)
         cout << (*it) << " ";
//cbegin()不可修改*it内容

rbegin(),rend() vs crbegin(),crend()-----区别就是r是reverse,c同const

deque<char> deq = {'a', 'b', 'c', 'd', 'e'};
     for (auto it = deq.rbegin(); it != deq.rend();it++){
         cout << *it << " ";
         (*it) += 1;
     }
     cout << endl;
     for (auto it = deq.crbegin(); it != deq.crend(); it++)
         cout << (*it) << " ";

front()和back()也就是队头和队尾

 deque<char> deq = {'b', 'a','b','b', 'c', 'b', 'e'};
     for (auto it = deq.begin()+1; it != deq.end();){
        if(*it==deq.front())//front();back()
            it = deq.erase(it);
        else
            it++;
     }

erase(it1,it2) [it1,it2)

deq.erase(deq.begin() + 1, deq.end() -1);

leecode:滑动窗口最大值

239. 滑动窗口最大值

法一：单调队列类解决

首先先看一下类中含有另一个类的对象用法

class triangle{
public:
    triangle(double a, double b) : a(a), b(b) {}
    double area()
    { // 计算面积
        return (1.0 / 2) * a * b;
    }

private:
    double a, b;
};
class pyramid{
public:
    // 传参是类对象的多参数
    pyramid(double a, double b, double c) : height(a), tri(b, c) {}
    double volume()
    { // 计算体积
        return (1.0 / 3) * height * tri.area();
    }

private:
    triangle tri; // 类triangle对象
    double height;
};
int main(){
    pyramid tmp(6, 12, 24);
    cout << tmp.volume();
    return 0;
}

解题：

直接建立一个单调递减队列的数据结构，然后入队和出队操作就调用函数

只需要考虑移动时的窗口中的数据，注意：单调队列的数据和原数据并不是吻合的

所以原数据窗口需要用到数组下标来决定：

[0,1,2,3,4,…,k-1],所以i-队头+1=k即：窗口头部下标为：i-k+1

class monoQueue{
public:
    /*建立单调递减队列--队头是最大值*/
    //入队
    void push(int x){
        while(!dq.empty()&&x>dq.back()){
            dq.pop_back();
        }
        dq.push_back(x);
    }
    //删除指定大小的队头
    void pop(int x){
        if(!dq.empty()&&dq.front()==x){
            dq.pop_front();
        }
    }
    //队头是最大值
    int max(){
        if(!dq.empty())
            return dq.front();
        throw "dq is empty()";
    }
private:
    deque<int> dq;
};
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> res;
        //从头开始遍历元素
        for(int i=0;i<nums.size();i++){
            //不足k个元素时，元素入队
            if(i<k-1){//0,..,k-2,k-1
               mo.push(nums[i]);
            }//已经装满k-1个元素
            else{
               mo.push(nums[i]);//移入新元素
               res.push_back(mo.max());
               mo.pop(nums[i-k+1]);
            }
        }
        return res;
    }
private:
    monoQueue mo;//单调队列成员
};

 vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> res;
        deque<int> dq;
        for(int i=0;i<nums.size();i++){
            if(i<k-1){
                while(!dq.empty() && nums[i]>dq.back()){
                    dq.pop_back();
                }
                dq.push_back(nums[i]);
            }
            else{
                while(!dq.empty() && nums[i]>dq.back()){
                    dq.pop_back();
                }
                dq.push_back(nums[i]);
                res.push_back(dq.front());
                if(dq.front()==nums[i-k+1]){
                    dq.pop_front();
                }
            }
        }
        return res;
    }

也可以在代码中表现出：单调队的性质

法二：用双端队列存下标

分析双指针，前缀和以及单调队列

双指针：维护的信息的一个点或者多个点
前缀和：维护的信息是一个区间

[l,r]的信息可以通过[0,r]和[0,l-1]的信息推导出

比如：

1 5 3 2 -1 —1 5最大值5，1 5 3 2 -1最大值5，但是得不出3 2 -1 最大值3,
单调队列：维护的信息是一个区间，一般与最值有关

 vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        //首先将[0,k-1]元素入栈，使得窗口大小为k
        deque<int> dq;//存下标,维护递减队列
        vector<int> res;
        for(int i=0;i<=k-1;i++){
            while(!dq.empty()&&nums[i]>nums[dq.back()]){
                dq.pop_back();
            }
            dq.push_back(i);
        }
        res.push_back(nums[dq.front()]);//存入第一个结果
        //接下来尝试前移窗口
        for(int i=k;i<nums.size();i++){
            while(!dq.empty()&&nums[i]>nums[dq.back()]){
                dq.pop_back();
            }
            dq.push_back(i);
            //合法性检查，判断当前单调队列队头是否在窗口内
            if(!dq.empty()&&i-dq.front()+1>k){
                dq.pop_front();
            }
            res.push_back(nums[dq.front()]);
        }
        return res;
    }

当然也可以合并成一个for,分为if,else

窗口不足k,一直更新单调栈
窗口大于k,每次加入一个新元素后，必须判断队头是否过期了

 vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int> dq; 
        vector<int> res;
        for (int i = 0; i < nums.size(); i++) {
            if (i <= k - 1) {
                while (!dq.empty() && nums[i] > nums[dq.back()]) {
                    dq.pop_back();
                }
                dq.push_back(i);
                if (i == k-1) {//注意k-1是第一个满足的
                    res.push_back(nums[dq.front()]);
                }
            }//if
            else {
                while (!dq.empty() && nums[i] > nums[dq.back()]) {
                    dq.pop_back();
                }
                dq.push_back(i);
                //合法性检查，判断当前单调队列队头是否在窗口内
                if (!dq.empty() && i - dq.front() + 1 > k) {
                    dq.pop_front();
                }
                res.push_back(nums[dq.front()]);
            }
        }
        return res;
    }

单调队列模板

for 数组中的每个元素：
    1：while/if(队头过期) 删除队头----这里i和队头下标距离大于窗口k就是过期了
    
    2：while(队尾破坏单调性) 删除队尾
    加入新元素----单调队列的新元素一定会入队，所以一定先去掉破坏单调性的
    
    if(满足条件)  计算答案----这里的条件指的是：i超过k-1
    
    //1和2根据实际条件，可以颠倒

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> res;
        deque<int> dq;
        for(int i=0;i<nums.size();i++){
            //队头进行合法性检查
            while(!dq.empty() && nums[i]>nums[dq.back()]){
                dq.pop_back();
            }
            dq.push_back(i);
            if(!dq.empty()&&i-dq.front()+1>k){
                //dq.top()不在终点为i的窗口内了
                dq.pop_front();
            }
            //合法结果存入res
            if(i>=k-1){
                res.push_back(nums[dq.front()]);
            }
        }
        return res;
    }

颠倒

for(int i=0;i<nums.size();i++){
         //1
         while(!dq.empty()&&i-dq.front()+1>k){
             dq.pop_front();
         }
         //2
         while(!dq.empty() && nums[i]>nums[dq.back()]){
             dq.pop_back();
         }
         dq.push_back(i);
         //3
         if(i>=k-1){
             res.push_back(nums[dq.front()]);
         }
     }

用优先队列实现

注意堆一定要存值，但是堆中的下标有意义，单调队列中，一定程度上保证了有序性，也就是i-k+1的位置是队头，但是堆不是这样的。所以要存两个信息

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        //定义大顶堆
        typedef pair<int,int> T;// using T=pair<int,int>;
        priority_queue<T> pq;
        vector<int> res;
        for(int i=0;i<=k-1;i++){
           pq.push(make_pair(nums[i],i));
        }
        res.push_back(pq.top().first);
        for(int i=k;i<nums.size();i++){
            pq.push(make_pair(nums[i],i));
            //判断堆头是否需要删除
            //注意用while,因为堆中可能多个元素在外面
            while(i-pq.top().second+1>k){
                pq.pop();
            }
            res.push_back(pq.top().first);
        }
        return res;
    }

因为堆中可能多个元素在外面,用while

while(i-pq.top().second+1>k)--------不可以用if

using 别名=类型;

优先队列

优先队列是以堆的形式来存储队列中的元素，并且每次在插入和删除数据时，会自动对数据进行排序

class PriorityQueue :public Heap{};

优先队列priority_queue在c++中的**#include**中

在O(1)的时间内找到最值元素，并且能在在O(logn)的时间内插入和删除元素。

初始化

priority_queue<T, Container, Compare>//类型，容器，比较函数
priority_queue<T> //直接输入元素则使用默认容器和比较函数

T就是Type为数据类型
Container是容器类型

Container必须是用数组实现的容器，比如vector,deque等等，但不能用 list

STL里面默认用的是vector
Compare是比较方法，类似于sort第三个参数那样的比较方式，可以自定义类型

//升序队列
priority_queue <int,vector<int>,greater<int> > q;//小顶堆，堆顶<其他
//降序队列
priority_queue <int,vector<int>,less<int> >q;//大顶堆，堆顶>其他
//greater和less是std实现的两个仿函数(就是使一个类的使用看上去像一个函数)

想象堆排序的原理:(大的下沉)

greater的第一个参数是当前元素，第二个参数是子节点，如果当前元素比子节点大，就下沉，所以是小顶堆。

常用函数

priority_queue<int> q;
//函数和栈常用函数类似
q.top();//取队列首元素，也就是堆顶元素
q.empty();//判断队列是否为空
q.size();//返回队列的元素个数
q.push(val);//向优先队列中插入一个元素
q.pop();//弹出队列头元素

例子

pair比较

先按照pair的first元素排序，first元素相等时，再按照second元素排序

#include <iostream>
#include <queue>
using namespace std;
int main()
{
    priority_queue<pair<int, char>> pq; // pq是大顶堆，默认第一个元素排序
    vector<int> aa = {100, 400, 200, 900, 300, 600};
    vector<char> bb = {'w', 'g', 'l', 'i', 'p', 'q'};
    for (int i = 0; i < 6; i++){
        pq.push(make_pair(aa[i], bb[i]));
    }
    while (!pq.empty()){
        cout << pq.top().first << "," << pq.top().second << endl;
        pq.pop();
    }
    return 0;
}

900,i
600,q
400,g
300,p
200,l
100,w

priority_queue< pair<char, int>,vector<pair<char, int>>,greater<pair<char,int>> >pq; // pq是小顶堆 
    vector<int> aa =  {'w','d','u','z','a','f'};
    vector<char> bb = {1,9,8,5,3,7};
    for (int i = 0; i < 6; i++){
        pq.push(make_pair(aa[i], bb[i]));
    }
    while (!pq.empty()){
        cout << pq.top().first << "," << pq.top().second << endl;
        pq.pop();
    }

注意：priority_queue<T, vector, greater >—这里用pair<>代替T

a,3
d,9
f,7
u,8
w,1
z,5

重载<

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
class T{
public:
    int a, b, c;
    T(int a,int b,int c):a(a),b(b),c(c){}
    //自定义比较
};
 bool operator <(const T& t1,const T& t2){//>要与greater<T>匹配
        return t1.c < t2.c;
    }
int main()
{
    priority_queue<T> pq;
    pq.push(T(1, 4, 7));
    pq.push(T(8, 3, 17));
    pq.push(T(9, 1, 9));
    pq.push(T(2, 2, 18));
    while(!pq.empty()){
        cout << pq.top().a << "," << pq.top().b << "," << pq.top().c << endl;
        pq.pop();
    }
    return 0;
}

2,2,18
8,3,17
9,1,9
1,4,7

class T{
public:
 int a, b, c;
 T(int a,int b,int c):a(a),b(b),c(c){}
 //自定义比较
 bool operator <(const T& t) const{//成员函数必须const修饰
     return c < t.c;
 }
};
/*bool operator <(const T& t1,const T& t2){//>要与greater<T>匹配
     return t1.c < t2.c;
}*/

类内重载必须加上const,这是一个重写的标准写法

class T{
public:
    int a, b, c;
    T(int a,int b,int c):a(a),b(b),c(c){}
    //类内友元函数方式
    friend bool operator <(const T& t1,const T& t2){
        return t1.c < t2.c;
    }
};

类内友元函数方式

注意：类内函数要加const,类外函数需要两个比较对象

大顶堆在重载运算符<之后，就可以不带参数判断

<和大顶堆匹配（less），因为小的下沉，自然就是大顶堆了

priority_queue<node, vector, less> pq;----正确
priority_queue<node, vector, greater> pq;----错误，因为没有greater

struct node{
    int x, y;
    node(int x=0,int y=0):x(x),y(y){}
};
//重载operator
bool operator<(const node& a,const node& b){
    return a.x < b.x;
}
int main()
{
    priority_queue<node> pq;
    for (int i = 0; i < 6;i++){
        int tmp1 = rand() % 10;
        int tmp2 = rand() % 20;
        cout << tmp1 << "," << tmp2 << endl;
        pq.push(node(tmp1,tmp2));
    };
    cout << "******" << endl;
    while(!pq.empty()){
        cout << pq.top().x << ":" << pq.top().y << endl;
        pq.pop();
    }
    return 0;
}

重载operator>后就可以定义小顶堆了

//重载operator
bool operator>(const node& a,const node& b){
 return a.x > b.x;
}
priority_queue<node, vector<node>, greater<node>> pq;

重载operator()

class node{
public:
    int a, b;
    node(int a=0,int b=0):a(a),b(b){}
};
class cmp{
public:
    bool operator()(const node& aa,const node& bb){
        return aa.b > bb.b;
    }
};
int main()
{
    priority_queue<node, vector<node>, cmp> pq;
    pq.push(node(1, 2));
    pq.push(node(3, 6));
    pq.push(node(4, 5));
    while(!pq.empty()){
        cout << pq.top().a << "," << pq.top().b << endl;
        pq.pop();
    }
    return 0;
}

1,2
4,5
3,6

看：2 5 6，因为>,大的下沉了，就变成小的了
class cmp{
public:
 bool operator()(const node& aa,const node& bb){
     return aa.a < bb.a;
 }
};
4,5
3,6
1,2

看：4 3 1，因为<,小的下沉了，就变成大的了

比较优先队列和sort()

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
class node{
public:
    int a, b;
    node(int a=0,int b=0):a(a),b(b){}
    //类内重载函数
    bool operator<(const node& x) const{//别忘了const
        return a < x.a;
    }
};
int main()
{
    node a(11, 33);
    node b(22, 44);
    node c(13, 25);
    node d(31, 16);
    vector<node> vec;
    vec.push_back(a);
    vec.push_back(b);
    vec.push_back(c);
    vec.push_back(d);
    priority_queue<node> pq;
    for(auto m:vec)
        pq.push(m);
    sort(vec.begin(), vec.end());//排序
    for(auto [k,v]:vec){//vec小的在前
        cout << k << "," << v << endl;
    }
    cout << endl;
    while(!pq.empty()){//pq小的下沉
        cout << pq.top().a << "," << pq.top().b << endl;
        pq.pop();
    }
    return 0;
}

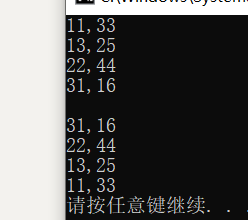
在这里插入图片描述