1. 题目描述

• 请实现一个函数，输入一个整数，输出该数二进制表示中1的个数。例如把9表示成二进制位1001，有2位是1，因此如果输入9，该函数输出2.
• 可以进这个链接练习——牛客网

2. 可能引起死循环的想法

• 这是一道很基本的考查二进制和位运算的面试题。
• 题目不是很难，面试官提出问题之后，我们很快就能形成一个基本的思路:先判断整数二进制表示中最右边一位是不是1。
• 接着把输入的整数右移一位，此时原来处于从右边数起的第二位被移到最右边了,再判断是不是1。
• 这样每次移动一位，直到整个整数变成0为止。现在的问题变成怎么判断一个整数的最右边是不是1了。
• 这很简单，只要把整数和1做位与运算看结果是不是0就知道了。
• 1除了最右边的一位之外所有位都是0。
• 如果一个整数与1做与运算的结果是1，表示该整数最右边一位是1，否则是0。
• 基于这个思路，我们很快就能写出如下代码:

#include <stdio.h>

int NumberOf1(int n)
{
	int count = 0;
	
	while (n != 0)
	{
		if (n & 1)
		{
			count++;
		}
		n >>= 1;
	}
	return count;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	printf("%d\n", NumberOf1(n));
	return 0;
}

• 当输入 9 时：

• 面试官看了代码之后可能会问:把整数右移一位和把整数除以2在数学上是等价的，那上面的代码中可以把右移运算换成除以2吗?答案是否定的。
• 因为除法的效率比移位运算要低得多，在实际编程中应尽可能地用移位运算符代替乘除法。
• 面试官接下来可能要问的第二个问题就是:上面的函数如果输入一个负数，比如 0x80000000，运行的时候会发生什么情况?
• 把负数0x80000000右移一位的时候并不是简单地把最高位的1移到第二位变成0x40000000而是0xC0000000。
• 这是因为移位前是个负数，仍然要保证移位后是个负数，因此移位后的最高位会设为1。
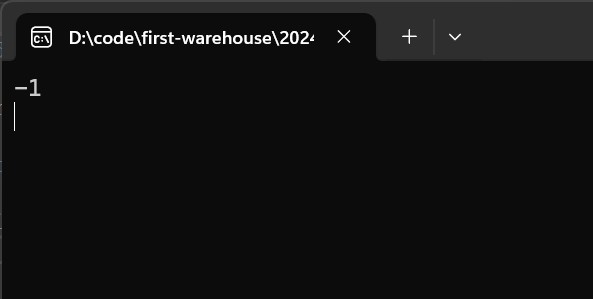
• 如果一直做右移运算，最终这个数字就会变成FFFFFFFF陷入死循环
• 当输入-1时：

3. 改进后的代码

• 为了避免死循环，我们可以不右移输入的数字 n。
• 首先把 n 和 1 做与运算，判断 n 的最低为是不是 1。
• 接着把 1 左移一位得到 2 ，再和 n 做与运算，就能判断 n 的次低位是不是 1……这样反复左移，每次都能判断 n 的其中一位是不是 1 了
• 基于这个思路，我们可以把代码修改如下：

#include <stdio.h>

int NumberOf1(int n)
{
	int count = 0;
	unsigned int flag = 1;
	
	while (flag != 0)
	{
		if (n & flag)
		{
			count++;
		}
		flag <<= 1;
	}
	return count;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	printf("%d\n", NumberOf1(n));
	return 0;
}

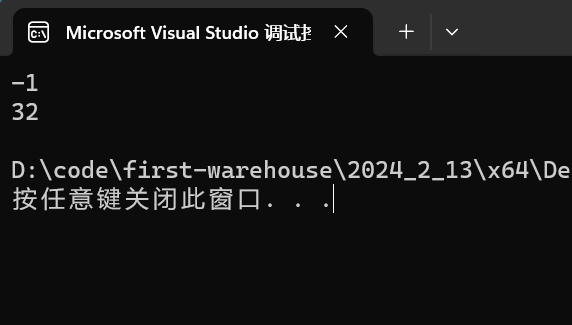
• 当输入 9 时：

• 当输入 -1 时：

4. 给面试官惊喜的代码

• 在分析这种算法之前，我们先来分析把一个数减去1的情况。
• 如果一个整数不等于0，那么该整数的二进制表示中至少有一位是1。
• 先假设这个数的最右边一位是1，那么减去1时，最后一位变成0而其他所有位都保持不变。
• 也就是最后一位相当于做了取反操作，由1变成了0。
• 接下来假设最后一位不是1而是0的情况。
• 如果该整数的二进制表示中最右边1位于第m位，那么减去1时，第m位由1变成0，而第m位之后的所有0都变成1，整数中第m位之前的所有位都保持不变。
• 举个例子:一个二进制数1100，它的第二位是从最右边数起的一个1。减去1后，第位变成0，它后面的两位0变成1，而前面的1保持不变，因此得到的结果是1011。
• 在前面两种情况中，我们发现把一个整数减去1，都是把最右边的1变成0。
• 如果它的右边还有0的话，所有的0都变成1，而它左边所有位都保持不变。
• 接下来我们把一个整数和它减去1的结果做位与运算，相当于把它最右边的1变成0。
• 还是以前面的1100为例，它减去1的结果是1011。
• 我们再把1100和1011做位与运算，得到的结果是1000。我们把1100最右
• 边的1变成了0，结果刚好就是1000。
• 我们把上面的分析总结起来就是:把一个整数减去1，再和原整数做与运算，会把该整数最右边一个1变成0。
• 那么一个数的二进制表示中有多少个1，就可以进行多少次这样的操作。基于这种思路，我们可以写出新的代码：

#include <stdio.h>

int NumberOf1(int n)
{
	int count = 0;
	
	while (n != 0)
	{
		n = n & (n - 1);
		count++;
	}

	return count;
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	printf("%d\n", NumberOf1(n));
	return 0;
}

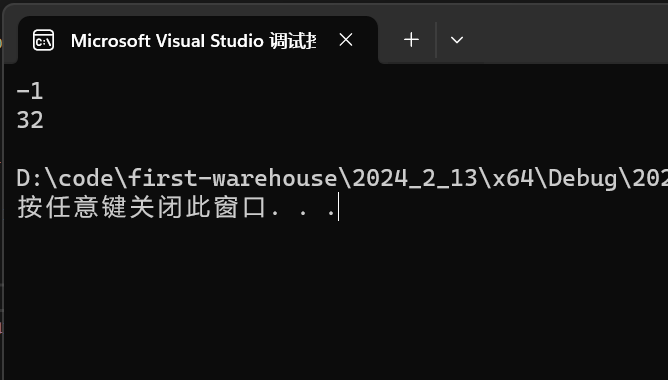
• 运行结果为：

最后，
恭喜你又遥遥领先了别人！