"Opportunities don't happen, you create them."
- Chris Grosser

1. 题目描述

2. 题目分析与解析
2.1 思路一——暴力求解
遇见这种可能刚开始没什么思路的问题,先试着按照人的思维来求解该题目。对于一个人来讲,我想要找到 s 字符串中包含 words 中所有字符串以任意顺序排列连接起来的子串的开始索引,那么我可能会有这种思路:
// 初始化wordsAndCount
for (String word : words) {
wordsAndCount.put(word, wordsAndCount.getOrDefault(word, 0) + 1);
}-
遍历字符串 s
-
对于每一个字符开头的与words中字符串长度相同的子串,尝试在words中匹配
-
如果匹配成功,就需要将words中当前字符串删除,下一次就从
当前字符 + words[i].length处开始继续匹配,以此循环,直到words为空,记录起始下标。 -
如果匹配失败,从下一个字符处继续重新匹配。
-
-
同时需要注意由于words中可能有相同的单词,因此我们需要记录如果是相同单词其出现的次数,这样就方便在遍历时删除,只需要将对应的值减一,当减到0就从words中删除该单词即可。初始化可以按照如下方式:

但是显然这种方法非常的耗时,因为对于每一个S字符串的字符你都需要查找是否匹配,最坏的情况下需要走完words的总长度,因此总遍历为S的长度 N 乘以 words的长度 M。但是起码我们能够解决问题,这能给我们一点自信再去想怎么优化,所以遇到问题先想想人怎么解决,没有思路的情况下就先不要太在意时间复杂度。
我按照如下的代码运行如预期会超时:


2.2 思路二——滑动窗口
对于这种一块一块的内容去对比的问题,我们应该敏锐的去想能不能用滑动窗口解决。刚好我在这也稍微总结一下什么情况下可以使用滑动窗口来解决,这样我们遇到新的题目就能更快速的想到可能的解决办法,再去尝试。
滑动窗口思想运用场景
滑动窗口技术是一种用于解决数组或列表相关问题的算法策略,特别适用于需要处理连续数据段的问题。这种技术广泛应用于各种场景,尤其是在需要优化时间和空间复杂度的场合。
-
最大/最小子数组问题:当你需要找到数组中某个大小的连续子数组,使得其和最大或最小时,滑动窗口技术可以有效地解决问题。
-
固定大小的问题:对于需要处理固定大小窗口的问题,如计算给定大小的窗口内的平均值、最大值或最小值,滑动窗口是一个理想的解决方案。
-
可变大小的问题:对于窗口大小不固定的问题,如找到数组中和至少为K的最短子数组,滑动窗口技术可以通过动态调整窗口大小来寻找最优解。
-
字符串匹配问题:在处理字符串时,如查找字符串中包含所有字符的最短子串,滑动窗口能够有效地跟踪字符出现的情况。
-
计数问题:当需要计数或统计特定条件下的连续子数组(或子序列)数量时,滑动窗口可以在遍历数组的同时维护这些统计信息。
-
双指针问题:在一些双指针问题中,滑动窗口可以视为一种特殊的双指针实现,尤其是当问题涉及到连续序列或子数组时。
-
连续序列问题:需要找到满足特定条件的连续序列时,如和为特定值的连续正数序列,滑动窗口提供了一种高效的解决方案。
滑动窗口技术之所以强大,是因为它能够在遍历数据的同时,通过调整窗口的大小或位置来动态地聚焦于问题的特定部分,从而在保持算法效率的同时减少不必要的重复计算。在解决这类问题时,滑动窗口不仅能够提供优化的解决方案,还能帮助理解和分析数据的连续性质。
回到题目
根据我的理解,其实滑动窗口的核心思想
-
就是把已经遍历过的内容存储在窗口里,这样对于下一次的遍历能够重复使用,减少再次遍历的开销。
而如果我们明确了使用滑动窗口来解决题目,那么我们就需要从以下几点着手:
-
窗口的大小:我们想把窗口指定多大比较合适?
-
窗口的移动:窗口可以向前“滑动”,每次移动可以是一步也可以是多步,这取决于问题的具体要求。窗口的移动使得算法能够逐步遍历整个数据集。我们应该怎么设置窗口的移动规则?
-
数据的复用:当窗口移动时,一些数据会从窗口中移出,同时会有新的数据加入到窗口中。窗口内的这些数据可以被复用来计算新的结果,从而避免了对已经遍历过的数据进行重复的计算。那我们怎么在这个问题中复用数据?
-
动态调整:窗口的大小是否需要动态调整?对于某些问题,窗口的大小可以根据特定的条件动态调整,比如在寻找满足条件的最小子序列长度时。这种动态调整能够帮助算法更加灵活地应对不同的问题需求。
根据上面几个点,我们可以一一来回答,但首先我们先回过头看看暴力解法为什么那么慢?
原因就是我每一次从一个字符开始,明明后面的很多内容遍历过了,但是在第二次for循环时我们还需要从第二个字符开始,重新走之前走的内容。因此我们就可以想一想是不是就可以指定一个窗口,用来容纳那些已经走过的地方,等到下一次遍历,我就直接使用这个窗口的数据。
但是这个窗口存什么呢?
窗口中存储的就是我们上一次for循环走过的尝试与words中内容进行匹配的数据,匹配不成功自然是从下一个位置开始,但是如果匹配成功了,那么下一次遍历我们就可以不需要再次匹配窗口中的数据。
因此就可以回答上面提出的几点问题了:窗口大小动态变化,窗口的移动一次移动一个words[i]的长度,但是这样还不够,因为如果每次跳过words[i].length个字符的话,我们对于每一个words[i]长度内部的起始位置我们会忽视掉,因为正如前几篇滑动窗口讲得一样,虽然滑动窗口很高效,但是它并没有偷懒,也就是它并没有忽视对每个位置的判断,只是将判断的过程简化了。如果我们以words[i]的长度为步长,会得到下图:
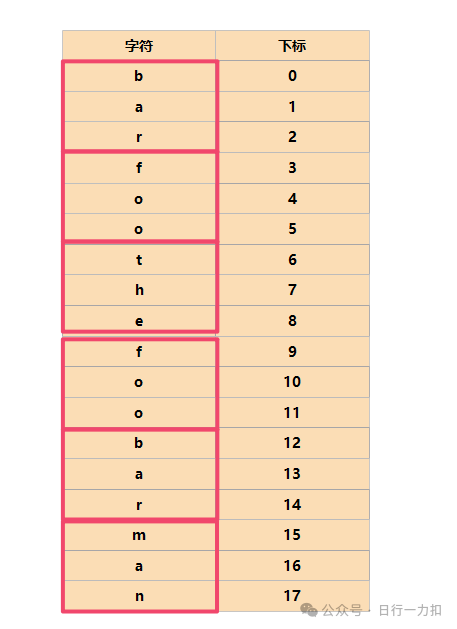
就是一个一个红色的框,但是我们忽视了如下紫色和绿色的框的起始位置的判断:
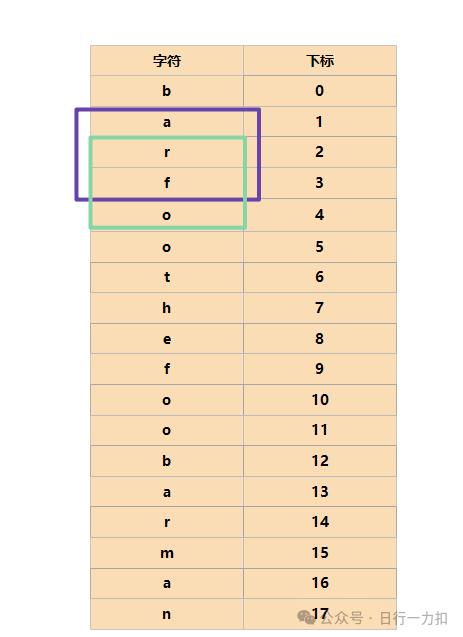
但是幸运的是,只需要words[i]个长度的框,就会出现重复的框,如下:
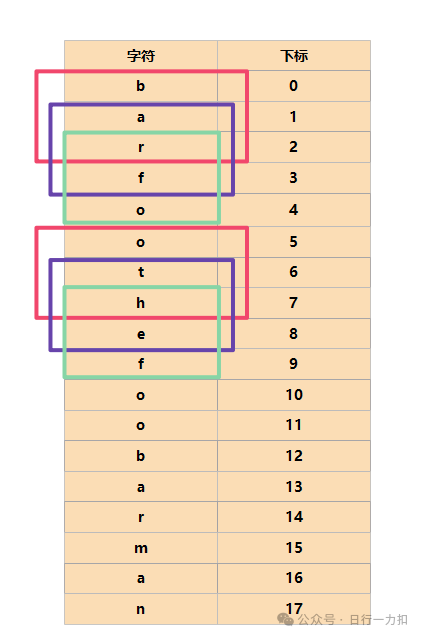
虽然可能解释起来用话说并不是特别清晰,但是通过图片我想大家应该知道是什么意思。因此我们的窗口就可以分为words[i].length类,比如 words = ["ab","cd","ef"],因为words[i].length = 2,所以定义2个窗口,就可以覆盖所有的范围。
接下来我们来考虑窗口如何利用数据:
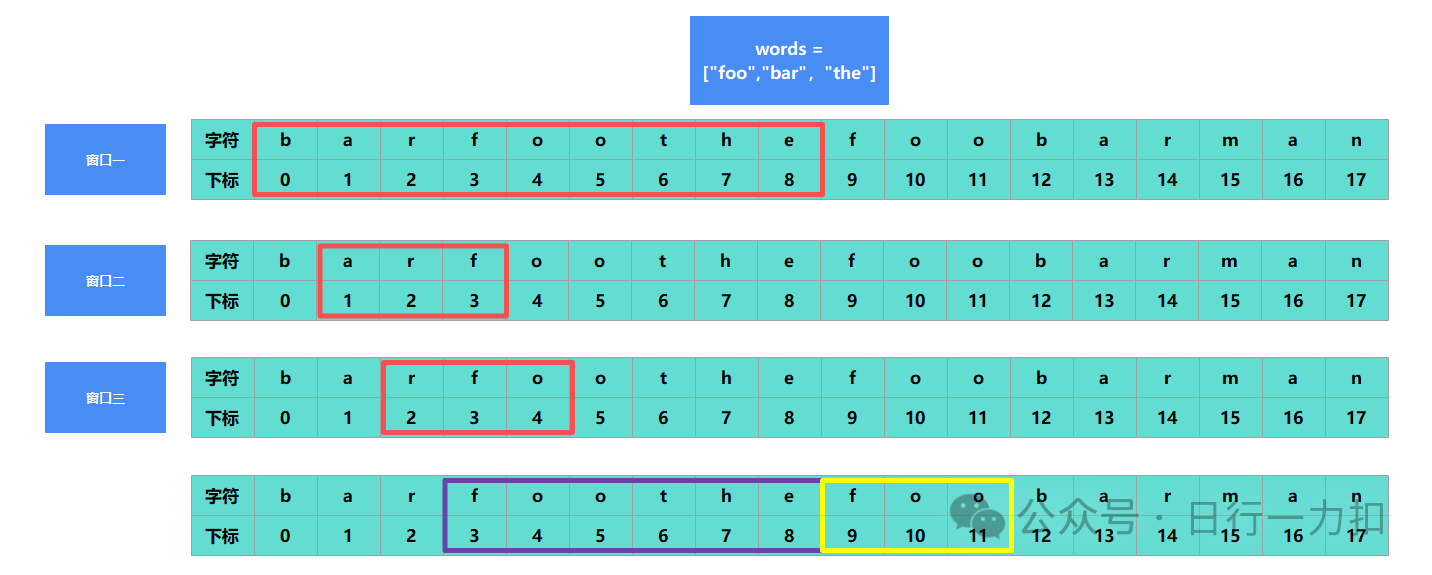
如上图所示,对于字符串S遍历过程中,指定三个窗口,如果能够匹配成功words中的某一个单词,就扩充窗口,这样在下一次遍历到窗口一类型的起始点的时候,如上紫色框所示内容就已经知道是能够匹配成功的,就无需再进行匹配,只需要判断黄色框是否能匹配即可。
因此我们基本可以得到如下的代码思路:(定义 words[i].length = n)
-
初始化,定义 n 个窗口,同时定义 n 个hashMap,用来存储words中的单词及其出现的个数(也可以放在每一次的外层for循环中)
-
外层for循环遍历窗口的个数(n个)
-
内层循环遍历不同的开头,比如对于窗口一,其遍历起始位置集合为:{ 0, 0 + n, 0 + 2n ...... }。移动右指针,每次加入一个单词,对应的一个记录窗口内部的单词计数的hashMap对应位置也加一。
-
如果当前单词对应窗口内部计数开始大于 存储words中的单词及其出现的个数,说明已经出现匹配不成功的情况了,因此就需要移动左指针,直到删除这个单词。
-
如果窗口内单词的出现次数,也就是
right-left的长度等于 words 中的单词的总长,说明找到了一个解。因为我们先对窗口内部的单词进行了计数,如果大于存储words中的单词及其出现的个数是会移动左指针的,而当任意一个窗口内部的单词的数量小于存储words中的单词数量,那长度肯定是不匹配的,所以只有窗口内部每一个的单词的数量完全匹配words中的单词数量,也就是right-left的长度等于 words 中的单词的总长,说明匹配成功!
-
3. 代码实现
3.1 暴力求解
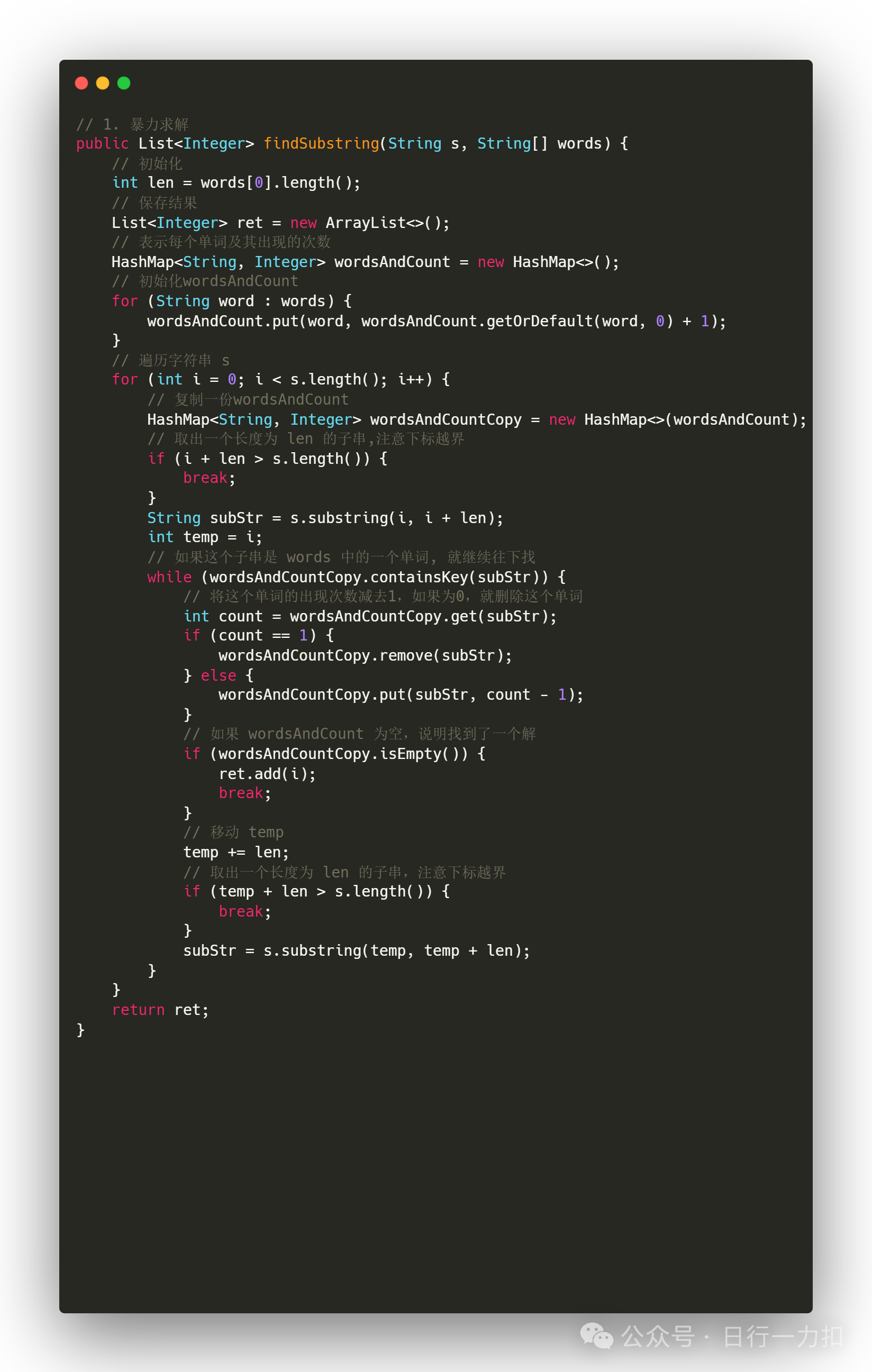
运行结果如上所示会超时!
3.2 滑动窗口
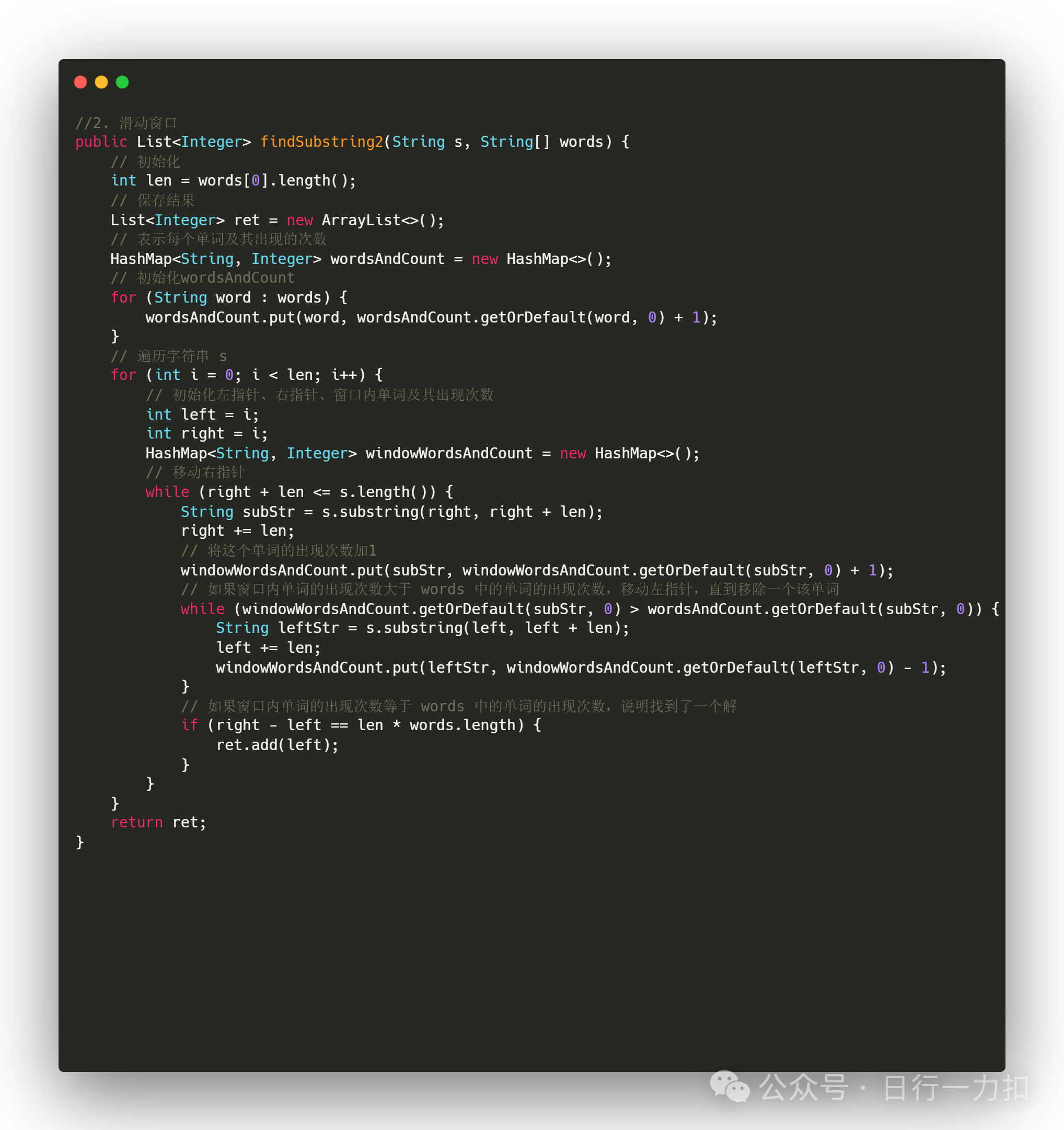
4. 相关复杂度分析
为了分析这两种解法的时间和空间复杂度,我们假定一些基本参数:
-
假设字符串
s的长度为N。 -
假设单词数组
words包含M个单词,每个单词的长度为L。 -
因此,所有单词串联形成的字符串长度是
M*L。
4.1 暴力解法的复杂度分析
时间复杂度:
-
对于字符串
s中的每个字符,算法尝试匹配所有单词串联形成的子串。 -
对于每个起始位置,算法最坏情况下需要比较
M*L长度的字符串。 -
因此,最坏情况下的时间复杂度是
O(N*M*L)。
空间复杂度:
-
需要一个HashMap来存储
words中单词及其出现的次数,其空间复杂度为O(M)。 -
每次循环时,都会创建一个
wordsAndCount的副本,因此空间复杂度保持为O(M)。
4.2 滑动窗口解法的复杂度分析
时间复杂度:
-
由于窗口的滑动是线性的,并且每个字符最多被访问两次(一次加入窗口,一次从窗口移除),这个复杂度可以优化为
O(N)。
空间复杂度:
-
使用了两个HashMap来存储
words中单词及其出现次数以及当前窗口内单词及其出现次数,空间复杂度为O(M)。
4.3 总结
-
暴力解法的时间复杂度较高,为
O(N*M*L),空间复杂度为O(M)。 -
滑动窗口解法通过优化遍历过程,将时间复杂度降低到
O(N),空间复杂度保持为O(M)。