给定 N
个闭区间 [ai,bi]
，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。

输出最小组数。

输入格式
第一行包含整数 N
，表示区间数。

接下来 N
行，每行包含两个整数 ai,bi
，表示一个区间的两个端点。

输出格式
输出一个整数，表示最小组数。

数据范围
1≤N≤105
,
−109≤ai≤bi≤109
输入样例：
3
-1 1
2 4
3 5
输出样例：
2

主要证明一下算法的合理性：
（1）这种选法cnt一定是一种合法的组数，而Ans是最小的合法方案（答案），因此Ans <= cnt。
（2）此时举一个特殊时刻：

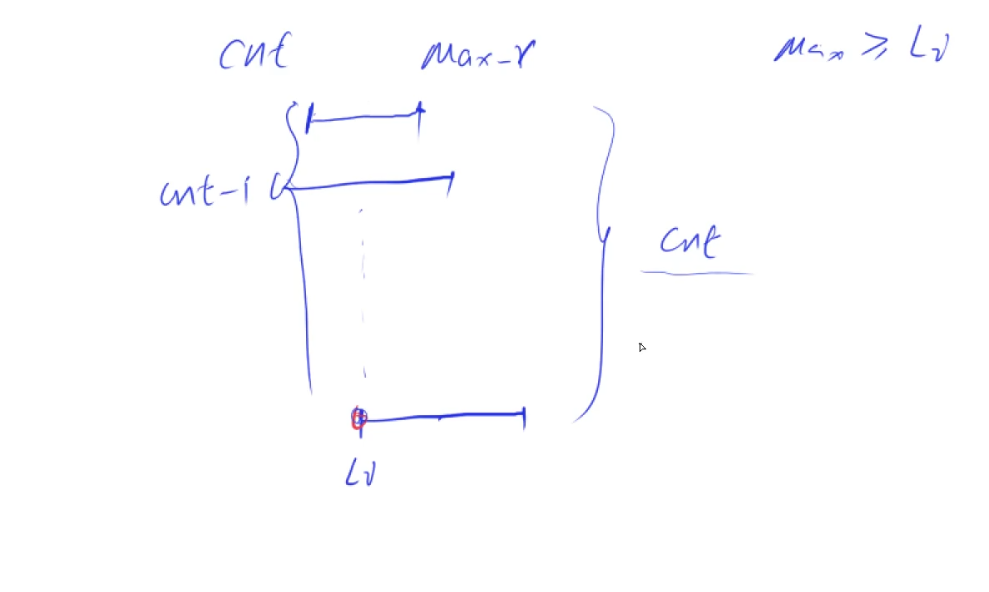
假设我们枚举到了第i个区间，然后这个区间的左端点和组里面存的最大右端点（Max_r）全满足Max_r >= l[i]，那么也就是cnt - 1个组都容不下当前区间，则这cnt个区间都必须在一个单独的组里面。因此所有组的可行方案一定是大于cnt的，证得Ans >= cnt；

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 100010;

int n;

struct Range
{
    int l, r;
    bool operator< (const Range &w) const
    {
        return l < w.l; 
    }
}range[N];

int main ()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }
    
    sort(range, range + n); // 按照左端点从小到大排序
    
    // 用小根堆来维护 所有组的右端点的最大值
    priority_queue<int, vector<int>, greater<int>> heap;
    for(int i = 0; i < n; i ++ )
    {
        auto r = range[i]; // 当前区间
        if(heap.empty() || heap.top() >= r.l) // 如果是空的 或者 堆顶元素都大于当前区间的左端点，就开一个新的组
            heap.push(r.r); // 新开一个组
        else // 否则的话说明当前的区间是可以放在某个组里面的
        {
            int t = heap.top(); // 放到最小值的那个组里面去？
            heap.pop();
            heap.push(r.r);
        }
    }
    
    printf("%d\n", heap.size());
    
    return 0;
}