机器学习 1:第 8 课
原文:
medium.com/@hiromi_suenaga/machine-learning-1-lesson-8-fa1a87064a53译者:飞龙
协议:CC BY-NC-SA 4.0
来自机器学习课程的个人笔记。随着我继续复习课程以“真正”理解它,这些笔记将继续更新和改进。非常感谢 Jeremy 和 Rachel 给了我这个学习的机会。
广义定义的神经网络
视频 / 笔记本
正如我们在上一课结束时讨论的那样,我们正在从决策树集成转向广义定义的神经网络。如你所知,随机森林和决策树受到一个限制,即它们基本上只是在做最近邻。它们所能做的就是返回一堆其他点的平均值。因此,它们无法外推,如果你在考虑如果我将价格提高 20%,而你以前从未定价到那个水平,或者明年的销售情况会发生什么,显然我们以前从未见过明年,外推是非常困难的。它也很难,因为它只能做大约对数 2 的 N 次决策,所以如果有一个时间序列需要拟合,需要 4 步才能到达正确的时间区域,然后突然它没有多少决策可以做了,所以它可以做的计算量有限。因此,它可以建模的关系复杂度有限。
问题:我可以问一个关于随机森林的另一个缺点吗?如果我们有一个数据作为分类变量,这些变量不是按顺序排列的,对于随机森林,我们对它们进行编码并将它们视为数字,假设我们有 20 个基数,那么随机森林给出的分割结果可能是小于 5 或小于 6。但如果类别不是按顺序排列(即没有任何顺序),那意味着什么?所以如果你有,比如说,让我们回到推土机,EROPS,带空调的 EROPS,OROPS,N/A 等,我们任意地将它们标记为 0 到 3。实际上我们知道真正重要的是是否有空调。那会发生什么?基本上它会说,如果我将 EROPS w A/C 和 OROPS 组合在一起,将 N/A 和 EROPS 组合在一起,这是一个有趣的分割,因为碰巧所有带空调的都会最终出现在右侧。做完这一步后,它会进一步注意到在 EROPS w A/C 和 OROPS 组中,它还需要将其进一步分成两组。最终它会到达那里。它会提取带有空调的类别。只是它需要更多的分割,比我们理想中希望的要多。所以这有点类似于它要建模一条线,只能通过大量分割并且只是近似地完成。
后续问题:那么随机森林对于不是连续的类别也可以吗?是的,它可以。只是在某些方面它不够理想,因为我们需要做比我们想要的更多的分割点,但它可以做到。它做得相当不错。因此,尽管随机森林确实存在一些缺陷,但它们非常强大,特别是因为它们几乎没有假设,所以很难出错。用随机森林赢得 Kaggle 比赛有点困难,但很容易进入前 10%。因此,在现实生活中,通常第三位小数并不是很重要,随机森林通常是你最终会做的事情。但对于像厄瓜多尔杂货比赛这样的事情,用随机森林很难得到好的结果,因为有一个巨大的时间序列组件,几乎所有的东西都是这两个大规模高基数的分类变量,即店铺和商品。因此,甚至没有太多的层可以用随机森林,每对店铺之间的差异在不同方面都是不同的,因此有一些事情即使对于随机森林来说也很难得到相对好的结果。
另一个例子是识别数字。你可以用随机森林得到可以接受的结果,但最终,空间结构之间的关系变得重要。你可能想要能够进行像查找边缘或其他计算一样的计算,这些计算会在计算中继续进行。因此,仅仅做一个聪明的最近邻类似于随机森林的方法并不理想。所以对于这样的事情,神经网络是理想的。神经网络被证明对于像厄瓜多尔杂货比赛(即通过店铺和商品预测销售额)和识别数字这样的事情非常有效。所以在这两个事情之间,神经网络和随机森林,我们覆盖了领域。我很长一段时间以来一直没有使用除了这两个方法之外的任何其他方法。在某个时候,我们将学习如何将这两种方法结合起来,因为你可以以非常酷的方式将它们结合起来。
MNIST [6:37]

这是 Adam Geitgey 的一张图片。一张图片只是一堆数字,每个数字都是从 0 到 255,暗的接近 255,亮的接近 0。这是来自 MNIST 数据集的一个数字的例子。MNIST 是一个非常古老的,就像神经网络的 hello world 一样。所以这是一个例子。

这里有 28x28 个像素。如果是彩色的话,会有三个 —— 一个红色的,一个绿色的,一个蓝色的。我们的任务是查看数字数组并弄清楚这是一个棘手的数字 8。我们如何做到这一点?
我们将使用一小部分 FastAI 的内容,并逐渐去除更多,直到最后,我们将从头开始实现自己的神经网络,自己的训练循环,以及自己的矩阵乘法。因此,我们将逐渐深入挖掘更多。
数据 [7:54]
from fastai.imports import *
from fastai.torch_imports import *
from fastai.io import *
path = 'data/mnist/'
import os
os.makedirs(path, exist_ok=True)
MNIST 的数据,这个非常著名的数据集的名称,可以从这里获取:
URL='http://deeplearning.net/data/mnist/'
FILENAME='mnist.pkl.gz'
def load_mnist(filename):
return pickle.load(gzip.open(filename, 'rb'), encoding='latin-1')
我们在 fastai.io 中有一个叫做 get_data 的东西,它会从 URL 中获取数据并将其存储在你的计算机上,除非它已经存在,否则它将继续使用它。我们这里有一个叫做 load_mnist 的小函数,它简单地加载数据。你会看到它是压缩的,所以我们可以使用 Python 的 gzip 来打开它。然后它也被 pickled,所以如果你有任何类型的 Python 对象,你可以使用这个内置的 Python 库叫做 pickle 来将其转储到你的磁盘上,分享它,稍后加载它,你会得到与开始时相同的 Python 对象。你已经看到了类似于 Pandas 的 feather 格式的东西。Pickle 不仅仅适用于 Pandas,也不仅仅适用于任何东西,它基本上适用于几乎每个 Python 对象。这可能会引发一个问题,为什么我们不为 Pandas 的 DataFrame 使用 pickle。答案是 pickle 适用于几乎每个 Python 对象,但对于几乎任何 Python 对象来说,它可能不是最佳选择。因此,因为我们正在查看具有超过一亿行的 Pandas DataFrames,我们真的希望快速保存,所以 feather 是专门为此目的设计的格式,因此它会非常快速地完成。如果我们尝试 pickle 它,那将需要更长的时间。另外请注意,pickle 文件仅适用于 Python,因此你不能将它们交给其他人,而 feather 文件可以传递。所以值得知道 pickle 的存在,因为如果你有一些字典或某种对象漂浮在周围,你想要稍后保存或发送给其他人,你总是可以将其 pickle 化。所以在这种特殊情况下,deeplearning.net 的人们很友好地提供了一个 pickled 版本。
Pickle 随着时间的推移有些变化,所以像这样的旧 pickle 文件(这是 Python 2 的一个),你实际上必须告诉它是使用这个特定的 Python 2 字符集编码的。但除此之外,Python 2 和 3,你通常可以打开彼此的 pickle 文件。
get_data(URL+FILENAME, path+FILENAME)
((x, y), (x_valid, y_valid), _) = load_mnist(path+FILENAME)
一旦我们加载了这个,我们就像这样加载 ((x, y), (x_valid, y_valid), _)。所以我们这里正在做的事情叫做解构。解构意味着 load_mnist 给我们返回了一个元组的元组。如果在等号的左边有一个元组的元组,我们可以填充所有这些内容。所以我们得到了一个训练数据的元组,一个验证数据的元组,以及一个测试数据的元组。在这种情况下,我不关心测试数据,所以我把它放到一个名为 _ 的变量中,Python 的人们倾向于认为这是一个特殊的变量,我们把要丢弃的东西放进去。它实际上并不特殊,但非常常见。如果你看到有东西被赋值给下划线,那可能意味着你只是要丢弃它。
顺便说一下,在 Jupyter 笔记本中它确实有一个特殊的含义,即你计算的最后一个单元格始终在下划线中可用。但这是一个独立的问题。
然后元组中的第一件事本身就是一个元组,所以我们将把它放入 x 和 y 中作为我们的训练数据,然后第二个元组放入 x 和 y 中作为我们的验证数据。所以这就是所谓的解构,它在许多语言中都很常见。有些语言不支持它,但那些支持的语言,生活会变得更容易。一旦我看到一些新的数据集,我就会查看我得到了什么。它是什么类型?Numpy 数组。它的形状是什么?50,000 x 784。那么因变量呢?那是一个数组,它的形状是 50,000。
type(x), x.shape, type(y), y.shape
'''
(numpy.ndarray, (50000, 784), numpy.ndarray, (50000,))
'''
我们之前看到的 8 的图像不是长度为 784,而是大小为 28 乘以 28。所以这里发生了什么?事实证明,他们只是将第二行连接到第一行,将第三行连接到第二行,将第四行连接到第三行。换句话说,他们将整个 28 乘以 28 展平成一个单一的一维数组。这有意义吗?所以它的大小将是 28²。这绝对不是正常的,所以不要认为你看到的一切都会是这样。大多数时候,当人们分享图像时,他们会将它们分享为 JPEG 或 PNG 格式,你加载它们,你会得到一个漂亮的二维数组。但在这种特殊情况下,出于某种原因,他们拿出来的东西被展平成了 784。这个“展平”这个词在处理张量时非常常见,所以当你展平一个张量时,这意味着你将它转换为比你开始的更低秩的张量。在这种情况下,我们为每个图像开始时是一个秩为 2 的张量(即矩阵),然后我们将每个图像转换为一个秩为 1 的张量(即向量)。所以整体来说,整个东西是一个秩为 2 的张量,而不是一个秩为 3 的张量。
所以只是为了提醒我们这里的行话,这在数学中我们会称之为向量。在计算机科学中,我们会称之为一维数组,但是因为深度学习的人们必须表现得比其他人更聪明,我们不得不称之为秩为 1 的张量。它们基本上意思相同,除非你是物理学家——在这种情况下,这意味着其他事情,你会对深度学习的人们感到非常生气,因为你会说“这不是张量”。所以就是这样。不要责怪我。这只是人们说的话。

所以这要么是一个矩阵,要么是一个二维数组,要么是一个秩为 2 的张量。

一旦我们开始进入三维,我们开始用完数学名字,这就是为什么我们开始友好地说秩为 3 的张量。所以实际上,没有什么特别的关于向量和矩阵使它们比秩为 3 或秩为 4 的张量更重要。所以我尽量不使用向量和矩阵这些术语,因为我真的不认为它们比其他秩的张量更特别。所以习惯将numpy.ndarray (50,000, 784)看作秩为 2 的张量是很好的。
然后是行和列。如果我们是计算机科学人员,我们会称之为零维和一维。但如果我们是深度学习人员,我们会称之为轴零和轴一。然后为了更加混淆,如果你是一个图像人员,列是第一个轴,行是第二个轴。

所以如果你想到电视,1920 乘以 1080——列乘以行。其他人包括深度学习和数学家,行乘以列。所以如果你使用 Python 图像库,你会得到列乘以行;几乎其他所有情况,行乘以列。所以要小心。[一个学生问“为什么他们这样做?”]因为他们讨厌我们,因为他们是坏人,我猜😆
在深度学习中有很多,许多不同领域汇集在一起,如信息论、计算机视觉、统计学、信号处理,最终形成了深度学习中的这种混杂的命名法。通常,每个版本的事物都会被使用,所以今天,我们将听到一些被称为负对数似然或二项式或分类交叉熵的东西,这取决于你来自哪里。我们已经看到了一些被称为独热编码或虚拟变量的东西,这取决于你来自哪里。实际上,这只是相同的概念在不同领域中有点独立地被发明,最终它们找到了通往机器学习的道路,然后我们不知道该如何称呼它们,所以我们称它们为以上所有的东西——就像这样。所以我认为这就是计算机视觉中的行和列发生的事情。
归一化
有这样一个概念,即对数据进行归一化,即减去均值并除以标准差。一个问题给你。通常,归一化数据很重要,这样我们就可以更容易地训练模型。你认为在训练随机森林时,归一化独立变量是否重要呢?
学生:老实说,我不知道为什么我们不需要归一化,我只知道我们不需要。
好的,有人想想为什么吗?真正的关键是,当我们决定在哪里分割时,唯一重要的是顺序。就像唯一重要的是它们是如何排序的,所以如果我们减去均值除以标准差,它们仍然按相同的顺序排序。所以记住当我们实现随机森林时,我们说对它们进行排序,然后完全忽略值。我们只是说现在一次添加一个来自依赖变量的东西。所以随机森林只关心独立变量的排序顺序。它们根本不关心它们的大小。这就是为什么它们对异常值非常免疫的原因,因为它们完全忽略了它是异常值,它们只关心哪个比其他东西更高。所以这是一个重要的概念。它不仅出现在随机森林中。它也出现在一些指标中。例如,ROC 曲线下面积,你会经常遇到,ROC 曲线下面积完全忽略了比例,只关心排序。当我们做树状图时,我们看到了另一种情况。斯皮尔曼相关是一种秩相关——只关心顺序,不关心比例。所以随机森林的许多美好之处之一是我们可以完全忽略许多这些统计分布问题。但是对于深度学习来说不行,因为在深度学习中,我们试图训练一个参数化模型。所以我们需要对数据进行归一化。如果不这样做,那么创建一个有效训练的网络将会更加困难。
所以我们抓取我们训练数据的均值和标准差,减去均值,除以标准差,这给我们一个均值为零,标准差为一的结果。
mean = x.mean()
std = x.std()
x=(x-mean)/std
mean, std, x.mean(), x.std()
'''
(0.13044983, 0.30728981, -3.1638146e-01, 0.99999934)
'''
现在对于我们的验证数据,我们需要使用训练数据的标准差和均值。我们必须以相同的方式对其进行标准化。就像分类变量一样,我们必须确保它们的相同索引映射到随机森林中的相同级别。或者缺失值,我们必须确保在替换缺失值时使用相同的中位数。你需要确保你在训练集中做的任何事情,在测试和验证集中都要完全相同。所以在这里,我减去了训练集的均值并除以训练集的标准差,所以这不是完全是零和一,但它非常接近。总的来说,如果你发现你在验证集或测试集上尝试某些东西,而它比你的训练集差得多得多,那可能是因为你以不一致的方式进行了标准化或编码类别或其他一些不一致的方式。
x_valid = (x_valid-mean)/std
x_valid.mean(), x_valid.std()
'''
(-0.0058509219, 0.99243325)
'''
查看数据[22:03]
让我们来看一下这些数据。所以我们在验证集中有 10,000 张图像,每张图像都是长度为 784 的秩为 1 的张量。
x_valid.shape(10000, 784)
为了显示它,我想将它转换为一个 28x28 的秩为 2 的张量。Numpy 有一个 reshape 函数,它接受一个张量并将其重塑为你请求的任何大小的张量。现在如果你考虑一下,你只需要告诉它有D个轴,你只需要告诉它你想要的D-1个轴,因为最后一个,它可以自己算出来。所以总共,这里一共有 10,000 乘以 784 个数字。所以如果你说我希望我的最后一个轴是 28x28,那么你可以算出(第一个轴)这必须是 10,000,否则它就不会适合。所以如果你放-1,它会说让它尽可能大或尽可能小以使其适合。所以你可以看到,它算出来必须是 10,000。你会看到这种方法在神经网络软件的预处理中经常使用。我可以在这里写 10,000,但我试图养成一种习惯,就是每当我提到输入中有多少项时,我倾向于使用-1,因为这意味着以后我可以使用子样本,这段代码不会出错。如果它是不平衡的,我可以进行一些分层抽样,这段代码不会出错。所以通过在这里使用-1 这种大小,它使得以后的更改更具弹性。这是一个很好的习惯。
x_imgs = np.reshape(x_valid, (-1,28,28)); x_imgs.shape(10000, 28, 28)
能够取张量并重新塑形、改变轴线等等的想法是你需要能够完全不假思索地做到的[23:56]。因为这种情况会经常发生。比如,这里有一个例子。我尝试读取一些图像,它们是扁平化的,我需要将它们重新塑形成一堆矩阵——好的,重新塑形。我用 OpenCV 读取了一些图像,结果发现 OpenCV 按照蓝绿红的顺序排列通道,其他所有的都希望它们是红绿蓝的。我需要颠倒最后一个轴。如何做到这一点?我用 Python 图像库读取了一些图像。它将它们读取为行、列、通道,PyTorch 希望通道、行、列。我该如何转换。所以这些都是你需要能够不假思索地做到的事情,就像立刻就能做到。因为这种情况经常发生,你绝不想坐在那里想了很久。所以确保你在这一周花很多时间练习今天你将看到的所有东西:重新塑形、切片、重新排序维度等等。所以最好的方法是自己创建一些小张量,开始思考,比如我应该尝试什么。
问题:在归一化时,您说许多机器学习算法在数据归一化时表现更好,但您也刚刚说过尺度并不重要?我说对于随机森林来说并不重要。因此,随机森林只会根据顺序输出结果,所以我们喜欢它们。我们喜欢随机森林是因为它们对分布假设不太担心。但我们现在不是在做随机森林,我们在做深度学习。而深度学习确实会在乎尺度。
问题:如果我们有参数化,那么我们应该进行尺度调整。如果我们有非参数化,我们就不需要进行尺度调整?不完全是这样。因为像 k 最近邻是非参数化的,尺度很重要,所以我会说涉及树的事情通常只会在某个点进行分割,所以你可能不在乎尺度,但你可能需要考虑这是一个使用顺序还是使用具体数字的算法。
问题:您能直观解释一下为什么它需要尺度吗,因为这可能会澄清一些问题?直到我们开始进行随机梯度下降时才需要,所以我们会讲到那一点。所以现在,我们只能说相信我的话。
问题:您能解释一下尺度是什么意思吗?因为当我想到尺度时,我认为所有数字应该大致相同大小。在我们进行深度学习时,猫和狗的情况是这样的,你可能有一只小猫和一只大猫,但它仍然知道它们都是猫?我想这是语言被重载的问题之一。在计算机视觉中,当我们对图像进行缩放时,实际上是增加了猫的大小。在这种情况下,我们正在缩放实际的像素值。因此,在这两种情况下,缩放意味着使某物变大和变小。在这种情况下,我们将数字从零到 255,并使它们的平均值为零,标准差为一。
问题:您能解释一下是按列还是按行?一般来说,当您进行缩放时,不仅仅考虑图像,而是输入到机器学习的内容。好的,当然。这有点微妙,但在这种情况下,我只有一个平均值和一个标准差。所以基本上,平均有多少黑色。因此,平均而言,我们有一个平均值和一个标准差跨越所有像素。在计算机视觉中,我们通常会按通道进行操作,所以通常会有一个数字代表红色,一个数字代表绿色,一个数字代表蓝色。一般来说,您需要为每个您希望表现不同的事物准备不同的归一化系数。因此,如果我们像处理一个结构化数据集,其中包括收入、公里数和孩子数量,您需要为这些事物准备三个单独的归一化系数,因为它们是非常不同的事物。因此,在这里有点领域特定。在这种情况下,所有像素都是灰度级别,因此我们只有一个缩放数字。而在其他情况下,如果它们是红色与绿色与蓝色,您需要以不同方式缩放这些通道。
问题:所以我有点难以想象如果在这种情况下不进行归一化会发生什么。我们会讨论到那里。这就是 Yannet 所说的为什么我们要归一化的原因,目前我们正在归一化是因为我说我们必须这样做。当我们开始研究随机梯度下降时,我们基本上会发现,如果你…基本上为了稍微提前一点,我们将会通过一堆权重进行矩阵乘法。我们将以这样一种方式选择这些权重,以便当我们进行矩阵乘法时,我们将尝试保持数字与它们最初的规模相同。这基本上需要我们知道初始数字的规模。因此,如果我们知道它们一直是均值为零,标准差为一,那么就更容易为许多不同类型的输入创建一个单一的神经网络架构。这将是简短的答案。但我们将学到更多关于它的知识,如果在几节课后你仍然不太明白为什么,让我们回过头来讨论,因为这是一个非常有趣的话题。
问题:我试图可视化我们正在使用的坐标轴。所以在绘图中,当你写x_valid.shape时,我们得到了 10,000 乘以 784。这意味着我们带入了那个维度的 10,000 张图片吗?是的,确切地说。问题继续:在下一行,当你选择重塑时,为什么将 28、28 作为 Y 或 Z 坐标?或者它们按照那个顺序有什么原因吗?

是的,有的。几乎所有的神经网络库都假设第一个轴相当于一行。就像一个单独的东西,它是一个句子或一幅图像或销售示例。所以我希望每个图像都是第一个轴的单独项目。然后,这样就为图像的行和列留下了另外两个轴。这是完全标准的。我认为我从来没有见过一个不是这样工作的库。
问题:在归一化验证数据时,我看到你使用了 x 数据的均值和标准差(即训练数据)。我们不应该使用验证数据的均值和标准差吗?不,因为你看,那样的话,你将使用不同的数字对验证集进行归一化,因此现在这个像素的值在验证集中的含义与在训练集中的含义不同。这就好像如果我们将一周的天数编码,使得星期一在训练集中是 1,在验证集中是 0。现在我们有了两组不同的数据,其中相同的数字具有不同的含义。
让我举个例子。假设我们正在处理全彩色图像,我们的训练集包含绿色青蛙、绿色蛇和灰色大象。我们正在训练以弄清楚它们各自是什么。然后我们使用每个通道的均值进行了归一化。然后我们有一个验证集和一个测试集,里面只有绿色青蛙和绿色蛇。如果我们使用验证集的统计数据进行归一化,我们最终会说平均而言都是绿色。所以我们会去除所有的绿色,因此我们现在将无法有效地识别绿色青蛙和绿色蛇。所以我们实际上希望使用我们训练时使用的相同的归一化系数。对于那些正在学习深度学习课程的人,我们实际上做得更多。当我们使用预训练的网络时,我们必须使用原始作者训练时使用的相同的归一化系数。因此,这个数字在你使用它的每个数据集中都需要有一致的含义。这意味着当你查看测试集时,你需要根据训练集的均值和标准差对测试集进行归一化。
show(x_imgs[0], y_valid[0])

所以验证 y 值只是一个长度为 10,000 的秩为 1 的张量。记住这是一种奇怪的 Python 事情,一个包含这一个东西的元组需要一个尾随逗号。所以这是一个长度为 10,000 的秩为 1 的张量。
y_valid.shape(10000,)
这里有一个例子。只是一个数字 3。这就是我们的标签。
y_valid[0]
'''
3
'''
切片
这里是另一件你需要能够做到熟练的事情。切片成一个张量。在这种情况下,我们用 0 切片到第一个轴,这意味着我们正在获取第一个切片。因为这是一个单一数字,这将减少张量的秩一次。它将把一个 3 维张量变成一个 2 维张量。所以你可以看到,这现在只是一个矩阵。然后我们将抓取 10 到 14 行,10 到 14 列,这就是它。所以这是你需要非常熟练的事情——抓取片段,查看数字,查看图片。
x_imgs[0,10:15,10:15]
'''
array([[-0.42452, -0.42452, -0.42452, -0.42452, 0.17294],
[-0.42452, -0.42452, -0.42452, 0.78312, 2.43567],
[-0.42452, -0.27197, 1.20261, 2.77889, 2.80432],
[-0.42452, 1.76194, 2.80432, 2.80432, 1.73651],
[-0.42452, 2.20685, 2.80432, 2.80432, 0.40176]], dtype=float32)
'''
这里是第一张图像的一小部分的例子。所以你应该习惯这样的想法,如果你在处理像图片或音频这样的东西,这是你的大脑真的很擅长解释的东西。所以尽可能经常展示你正在做的事情的图片。但也记住在幕后它们是数字,所以如果出现奇怪的情况,打印出一些实际的数字。你可能会发现其中一些变成了无穷大,或者它们全都是零,或者其他什么。所以在探索数据时利用这个交互式环境。
问题:只是一个快速的语义问题。为什么当它是一个秩为 3 的张量时,它被存储为 XYZ 而不是对我来说,将它存储为 2D 张量的列表会更有意义?它不是存储为任何一种。所以让我们把这看作是一个 3D。这里是一个 3D。所以一个 3D 张量被格式化为基本上显示一系列 2D 张量。

问题:但为什么不像x_imgs[0][10:15][10:15]那样?哦,因为那有不同的含义。这就是张量和不规则数组之间的区别。所以基本上如果你做类似a[2][3]这样的事情,那就是说取第二个列表项,然后从中获取第三个列表项。所以当我们有一个叫做不规则数组的东西时,我们倾向于使用这种方式,其中每个子数组的长度可能不同。而在其他情况下,我们有一个三维的单一对象。所以我们试图说我们想要它的哪一小部分。所以这个想法是一个单一的切片对象去抓取那一部分出来。
show(x_imgs[0,10:15,10:15])
plots(x_imgs[:8], titles=y_valid[:8])

这里有一些图像及其标签的例子。这种东西,你希望能够用 matplotlib 很快地完成。这将帮助你很多,这样你就可以看看 Rachel 在写plots时写的东西。我们可以使用 add_subplot 来创建这些小的独立图。你需要知道imshow是我们如何将一个 numpy 数组绘制成图片的。然后我们还添加了顶部的标题。所以就是这样。
def show(img, title=None):
plt.imshow(img, cmap="gray")
if title is not None: plt.title(title)
def plots(ims, figsize=(12,6), rows=2, titles=None):
f = plt.figure(figsize=figsize)
cols = len(ims)//rows
for i in range(len(ims)):
sp = f.add_subplot(rows, cols, i+1)
sp.axis('Off')
if titles is not None:
sp.set_title(titles[i], fontsize=16)
plt.imshow(ims[i], cmap='gray')
神经网络
让我们拿这些数据来尝试构建一个神经网络。对于那些已经在进行深度学习的人来说,这将是很多复习。神经网络实际上只是一个特定的数学函数或数学函数类,但它是一个非常重要的类,因为它具有支持所谓的通用逼近定理的属性。这意味着神经网络可以任意接近地逼近任何其他函数。换句话说,理论上,只要我们使它足够大,它就可以做任何事情。这与只能执行一种特定功能的函数如 3x + 5 非常不同。或者只能表示不同斜率的线条上下移动不同量的函数类ax + b。甚至函数ax² + bx + c + sin d也只能表示一个非常具体的关系子集。然而,神经网络是一个可以任意接近地表示任何其他函数的函数。
因此,我们要做的是学习如何取一个函数,比如ax + b,并学习如何找到其参数(在这种情况下为a和b),使其尽可能接近一组数据。这里展示了我们将在深度学习课程中查看的笔记本中的示例,基本上展示了当我们使用称为随机梯度下降来尝试设置a和b时会发生什么。基本上,我们将从一个随机的a和一个随机的b开始,然后我们基本上要弄清楚我是否需要增加或减少a来使线条接近点?我是否需要增加或减少b来使线条接近点?然后只需多次增加和减少a和b。这就是我们要做的,为了回答是否需要增加或减少a和b的问题,我们将取导数。因此,函数关于a和b的导数告诉我们当我们改变a和b时该函数将如何变化。这基本上就是我们要做的。但我们不会仅仅从一条线开始,想法是我们要逐步建立一个实际上具有神经网络的模型,因此这将是完全相同的想法,但由于它是一个无限灵活的函数,我们将能够使用这个完全相同的技术来适应任意复杂的关系。这基本上就是这个想法。

那么你需要知道的是,神经网络实际上是一件非常简单的事情。神经网络实际上是一个以输入为向量的东西,通过该向量进行矩阵乘积。因此,如果向量的大小为r,矩阵为r乘以c,则矩阵乘积将输出大小为c的结果。然后我们进行一种称为非线性的操作,基本上是我们要丢弃所有负值(即max(0, x))。然后我们将通过另一个矩阵乘法,再通过另一个max(0, x),再通过另一个矩阵乘法,直到最终得到我们想要的单个向量。换句话说,我们神经网络的每个阶段,关键的事情是进行矩阵乘法,换句话说,是一个线性函数。因此,基本上,深度学习中大部分的计算是大量的线性函数,但在每个线性函数之间,我们将用零替换负数。

问题:为什么我们要丢弃负数?我们将看到。简短的答案是,如果你对一个线性函数应用另一个线性函数,它仍然只是一个线性函数。所以这完全没有用。但是如果你丢弃负数,那实际上是一个非线性转换。结果表明,如果你对我们丢弃的负数应用一个线性函数,然后将其应用于创建神经网络的线性函数,结果就是这个东西可以任意接近任何其他函数。所以这个微小的差异实际上产生了很大的不同。如果你对此感兴趣,请查看我们涵盖这一内容的深度学习视频,因为我实际上展示了一个直观的证明,不是我创造的,而是 Michael Nielsen 创造的。或者,如果你想直接跳转到他的网站,你可以访问 Michael Nielsen 的通用逼近定理,他有一个非常好的步骤指南,其中包含许多动画,您可以看到为什么这样运作。
为什么你(是的,你)应该写博客
我觉得在互联网上开始技术写作最困难的事情就是发布你的第一篇文章。在这篇博客中,Rachel 实际上说她给年轻自己的最好建议是尽早开始写博客。她列举了为什么你应该这样做的原因,她写博客的一些地方对她和她的职业都很有帮助,以及一些如何开始的建议。
我记得当我第一次建议 Rachel 考虑写博客时,因为她有很多有趣的事情要说,起初她对自己能写博客这个想法感到有些惊讶。现在人们在会议上走过来对我们说:“你是 Rachel Thomas!我喜欢你的文章!”所以我看到了从“哇,我能写博客吗?”到被认为是一位优秀的技术作者的过渡。所以如果你仍然需要说服,或者想知道如何开始,请查看这篇文章。因为第一篇是最难的,也许你的第一篇应该是对你来说非常容易写的东西。所以可以是这样的,这是我们机器学习课程第 3 课的前 15 分钟的摘要 - 这是有趣的地方,这是我们学到的东西。或者可以是这样的,这是我如何使用随机森林解决实习中的特定问题的摘要。
我经常被问到“哦,我的实习,我的组织,我们有敏感的商业数据” - 没关系。只需找到另一个数据集,然后在那个数据集上进行操作以展示示例,或者对所有值进行匿名化并更改变量的名称等。您可以与雇主或实习合作伙伴交谈,以确保他们对您写的任何内容感到舒适。总的来说,人们喜欢他们的实习生写博客,讲述他们正在做的事情,因为这让他们看起来很酷。就像“嘿,我是在这家公司实习的,我写了这篇关于我所做的酷分析的文章”,然后其他人会说哇,这看起来是一家很棒的公司。一般来说,你会发现人们非常支持。此外,有很多数据集可用,所以即使您不能以您正在进行的工作为基础,您也肯定可以找到类似的东西。
PyTorch
我们将开始构建我们的神经网络。我们将使用一个叫做 PyTorch 的东西来构建它。PyTorch 是一个基本上看起来很像 numpy 的库。但是当你用 PyTorch 创建一些代码时,你可以在 GPU 上运行它而不是 CPU。所以 GPU 基本上可能会比你为 CPU 编写的代码快至少一个数量级,可能是数百倍,特别是涉及大量线性代数的东西。所以在深度学习、神经网络中,如果你没有 GPU,你可以在 CPU 上做,但会非常慢。Mac 没有我们可以用于这个的 GPU,因为我们需要 NVIDIA GPU。我实际上更希望我们可以使用你的 Mac,因为竞争是很好的。但 NVIDIA 确实是第一个创建支持通用图形编程单元(GPGPU)的 GPU 的公司,换句话说,这意味着使用 GPU 进行除了玩电脑游戏以外的事情。他们创建了一个叫做 CUDA 的框架。这是一个非常好的框架,在深度学习中几乎被普遍使用。如果你没有 NVIDIA GPU,你就不能使用它,目前没有任何 Mac 有 NVIDIA GPU。任何类型的大多数笔记本电脑都没有 NVIDIA GPU。如果你有兴趣在笔记本电脑上进行深度学习,好消息是你需要购买一台非常适合玩电脑游戏的笔记本电脑。有一个地方叫做XOTIC PC Gaming Laptops,你可以去那里购买一台适合进行深度学习的优秀笔记本电脑。你可以告诉你的父母,你需要这笔钱来进行深度学习。你通常会发现一大堆带有 predator 和 viper 等名称的笔记本电脑,上面有机器人和其他东西的图片。无论如何,话虽如此,我不认识很多人在笔记本电脑上做很多深度学习的。大多数人会登录到云环境中。我知道的最容易使用的是Crestle。使用 Crestle,你基本上可以注册,然后立即得到的第一件事就是你被直接投入到一个 jupyter 笔记本中。它支持 GPU,每小时 60 美分,所有 Fast AI 库和数据都已经可用。这使得生活变得非常容易。它比使用亚马逊网络服务选项的 AWS less 灵活,某些方面也不那么快。它的成本稍微高一点,每小时 90 美分而不是 60 美分。但很可能你的雇主已经在使用它,了解一下也是好的。他们在 GPU 周围有更多不同的选择,这是一个不错的选择。如果你是学生,可以搜索 github 学生包,你可以立即获得 150 美元的信用额度。所以这是一个开始的好方法。
问题:我想知道你对英特尔最近发布的一种提升常规软件包的开源方式的看法,他们声称这相当于使用底层 GPU。在你的 CPU 上,如果你使用他们的提升软件包,你可以获得相同的性能。实际上,英特尔制作了一些很棒的数值编程库,特别是这个叫做 MKL 的库,矩阵核心库。它们确实比不使用这些库更快,但如果你看一下性能随时间变化的图表,GPU 在过去 10 年中一直保持着大约每秒 10 次浮点运算,现在也是如此,而且通常价格只有相同性能的 CPU 的 1/5。因此,几乎所有进行深度学习的人基本上都是在 NVIDIA GPU 上进行的,因此使用除了 NVIDIA GPU 之外的任何东西目前都非常烦人——更慢、更昂贵、更烦人。我真的希望在这个领域尤其是在 AMD GPU 周围会有更多的活动,但 AMD 确实需要多年的追赶,所以可能需要一段时间。
评论:我只是想指出,你也可以购买一个 GPU 扩展器连接到笔记本电脑,这可能是在购买新笔记本电脑或 AWS 之前的第一步解决方案[52:46]。是的,我认为大约$300 左右,你可以购买一个插入到你的 Thunderbolt 端口的东西,如果你有一台 Mac,然后再花$500 或$600,你可以购买一个 GPU 插入其中。话虽如此,大约$1000,你就可以创建一个相当不错的基于 GPU 的台式机,所以如果你在考虑这个,Fast AI 论坛有很多帖子,人们在特定价格点上互相帮助。
总之,我建议一开始使用 Crestle,然后当你准备好投入一些额外的时间时,使用 AWS。要使用 AWS,当你到达那里时,去 EC2。AWS 上有很多东西,EC2 是我们可以按小时租用计算机的部分。

现在,我们需要一个基于 GPU 的实例。不幸的是,当你第一次注册 AWS 时,他们不会给你访问权限。所以去到 Limits(左上角)。

我们将使用的主要 GPU 实例称为 p2。所以滚动到 p2.xlarge,你需要确保数字不是零。如果你刚刚注册了一个新账户,它可能是零,这意味着你将无法创建一个。所以你必须去“请求限制增加”,其中的诀窍是当它问你为什么要增加限制时,输入“fast.ai”,因为 AWS 知道要留意,他们知道 fast.ai 的人是好人,所以他们会很快处理。通常需要一两天的时间。
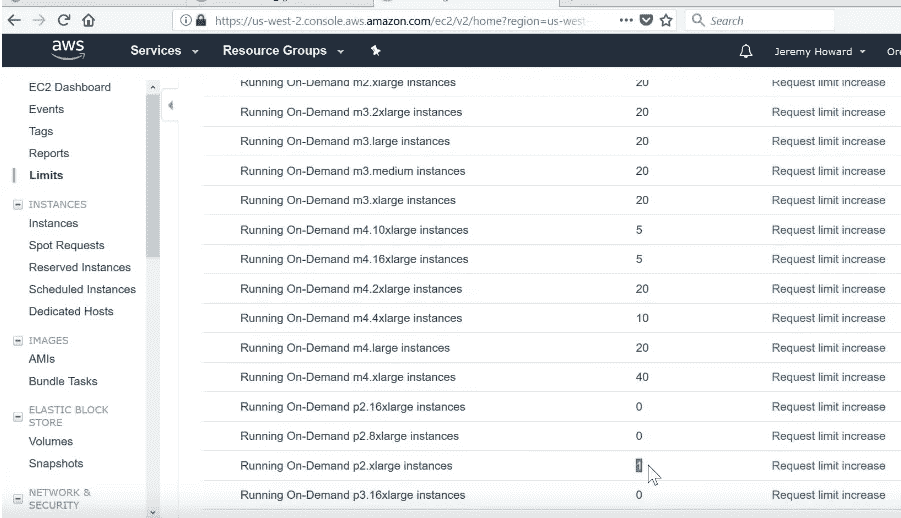
所以一旦你收到批准使用 p2 实例的邮件,你就可以回到这里并点击 Launch Instance:
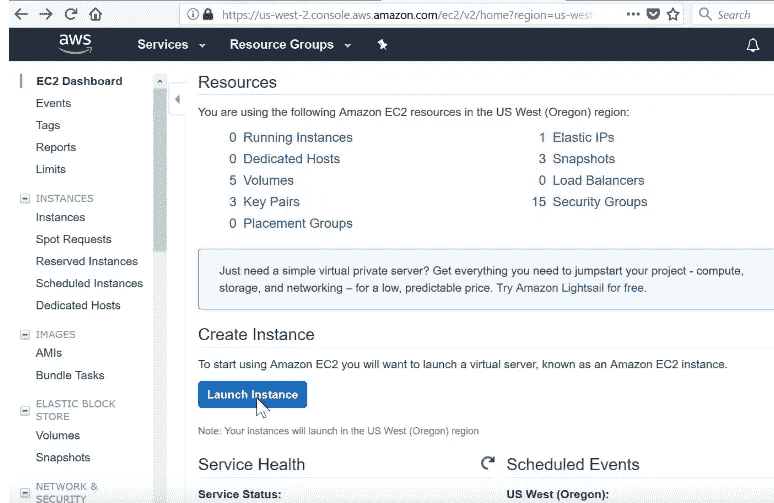
我们基本上设置了一个拥有一切你需要的东西。所以如果你点击 Community AMIs,AMI 是 Amazon Machine Image 的缩写——它基本上是一个完全设置好的计算机。所以如果你输入 fastai(连在一起),你会在这里找到 fastai DL part 1 v2 for p2。所以一切都准备就绪。
所以如果你点击 Select,它会问你想要什么样的计算机。所以我们必须说我想要一个“GPU 计算”类型,具体来说我想要 p2.xlarge。然后你可以点击“Review and Launch”。

我假设你已经知道如何处理 SSH 密钥和所有这些东西。如果你不知道,可以查看我们在线的入门教程和工作坊视频,或者在网上搜索 SSH 密钥。这是一个非常重要的技能。所以希望你通过所有这些,你可以在 GPU 上运行 Fast AI repo。如果你使用 Crestle,只需cd fastai2,repo 已经在那里,git pull。AWS,cd fastai,repo 已经在那里,git pull。如果是你自己的电脑,你只需要git clone,然后就可以开始了。
PyTorch 是预安装的,所以 PyTorch 基本上意味着我们可以编写看起来很像 numpy 的代码,但在 GPU 上运行速度非常快。其次,由于我们需要知道参数如何移动以改善我们的损失,我们需要知道函数的导数。PyTorch 有这个神奇的功能,任何你使用 PyTorch 库编写的代码,它都可以自动为你计算导数。所以我们在这门课程中不会涉及任何微积分。我在我的课程中从来没有看过微积分,也从来没有在我的工作中计算过导数,因为这些都是由库来完成的。只要你写好 Python 代码,导数就会被计算出来。所以成为一个有效的从业者,你真正需要了解的微积分只是导数是什么意思。你还需要知道链式法则,我们会讲到。
PyTorch 中的逻辑回归神经网络[57:45]
好的,所以我们将从上到下开始,创建一个神经网络,并假设很多东西。然后逐渐我们将深入研究每个部分。所以要创建神经网络,我们需要导入 PyTorch 神经网络库。有趣的是,PyTorch 并不叫 PyTorch——它叫 torch。所以torch.nn是负责神经网络的 PyTorch 子部分。我们将称之为 nn。我们将从 Fast AI 中导入一些部分,以使我们的生活变得更容易。
from fastai.metrics import *
from fastai.model import *
from fastai.dataset import *
import torch.nn as nn
这里是如何在 PyTorch 中创建神经网络的。最简单的神经网络,你说 Sequential。Sequential 意味着我现在要给你一个我想要在我的神经网络中的层的列表。所以在这种情况下,我的列表中有两个东西。第一件事说我想要一个线性层。现在线性层基本上会执行y = ax + b,但是矩阵矩阵相乘,而不是单变量。所以它基本上会执行一个矩阵乘积。矩阵乘积的输入将是一个长度为 28 乘以 28 的向量,因为这是我们有多少像素,输出需要是大小为 10(我们稍后会讨论原因)。目前这就是我们如何定义一个线性层。然后,我们将详细讨论这一点,但是几乎每个神经网络中的线性层之后都必须有一个非线性。然后我们将在一会儿学习这个特定的非线性,它被称为 softmax,如果你已经学过深度学习课程,你已经见过这个。这就是我们如何定义一个神经网络。这是一个两层神经网络。
net = nn.Sequential(
nn.Linear(28*28, 10),
nn.LogSoftmax()
).cuda()
还有一种隐含的额外第一层,即输入层,但是使用 PyTorch,你不必显式提及输入。但通常我们在概念上认为输入图像也是一种层。因为我们正在相当手动地进行操作,使用 PyTorch 我们没有利用 Fast AI 中构建你的东西的任何便利性,我们必须然后写.cuda(),这告诉 PyTorch 将这个神经网络复制到 GPU 上。从现在开始,该网络实际上将在 GPU 上运行。如果我们没有说,它将在 CPU 上运行。这给我们返回了一个神经网络——一个非常简单的神经网络。
数据[1:00:22]
然后我们将尝试将神经网络拟合到一些数据上。所以我们需要一些数据。Fast AI 有一个 ModelData 对象的概念,基本上是将训练数据、验证数据和可选的测试数据包装在一起的东西。所以要创建一个 ModelData 对象,你可以这样说:
-
我想创建一些图像分类器数据(
ImageClassifierData) -
我将从一些数组中获取它(
from_arrays) -
这是我将保存任何临时文件的路径(
path) -
这是我的训练数据数组(
(x,y)) -
这是我的验证数据数组(
(x_valid,y_valid))
这只是返回一个将所有这些包装起来的对象。所以我们将能够拟合到这些数据上。
md = ImageClassifierData.from_arrays(path, (x,y),(x_valid, y_valid))
现在我们有了一个神经网络和一些数据,我们将在一会儿回到这里,但基本上我们说我们想使用什么损失函数,想使用什么优化器,然后说拟合[1:01:07]。
loss=nn.NLLLoss()
metrics=[accuracy]
opt=optim.Adam(net.parameters())
我们说将这个网络net拟合到这个数据md上,每次遍历每个图像一次(n_epochs),使用这个损失函数loss,这个优化器opt,并打印出这些指标metrics。
fit(net, md, n_epochs=1, crit=loss, opt=opt, metrics=metrics)

这里说这是 91.8%的准确率。所以这就是最简单的神经网络。它正在创建一个矩阵乘法,然后是一个非线性,它试图找到这个矩阵的值(nn.Linear(28*28, 10)),基本上是尽可能好地拟合数据,最终预测这是 1,这是 9,这是 3。
损失函数[1:02:08]
所以我们需要一些关于“尽可能好”的定义。那个东西的一般术语叫做损失函数。所以损失函数是一个函数,如果这个函数更低,那么就更好。就像随机森林一样,我们有信息增益的概念,我们得选择用什么函数来定义信息增益,我们主要看的是均方根误差。大多数机器学习算法我们称之为类似于“损失”的东西。所以损失是我们如何评分我们有多好的东西。最终,我们将计算损失对我们正在乘以的权重矩阵的导数,以找出如何更新它。
我们将使用一种称为负对数似然损失(NLLLoss)的东西。负对数似然损失也被称为交叉熵,它们实际上是一样的。有两个版本,一个称为二元交叉熵或二元负对数似然,另一个称为分类交叉熵。它们是一样的,一个是当你只有一个零或一个依赖时,另一个是如果你有猫、狗、飞机或马,或者 0、1、到 9 等等。所以这里我们有交叉熵的二元版本:
def binary_loss(y, p):
return np.mean(-(y * np.log(p) + (1-y)*np.log(1-p)))
所以这里的定义是-(y * np.log(p) + (1-y)*np.log(1-p))。我认为理解这个定义的最简单方法可能是看一个例子。假设我们试图预测猫和狗。1 代表猫,0 代表狗。所以这里,我们有猫、狗、狗、猫([1, 0, 0, 1])。这是我们的预测([0.9, 0.1, 0.2, 0.8])。我们说 90%确定是猫,90%确定是狗,80%确定是狗,80%确定是猫。所以我们可以通过调用我们的函数来计算二元交叉熵。
对于第一个,我们有y=1,p=0.9(即(1 * np.log(0.9),因为第二项被跳过了)。对于第二个,第一部分被跳过(乘以 0),第二部分将是(1-0)*np.log(0.9)。换句话说,这个的第一部分和第二部分将给出完全相同的数字,这是有道理的,因为第一个我们说我们对是猫 90%有信心,而实际上是,第二个我们说我们对是狗 90%有信心,而实际上是。所以在每种情况下,损失都来自于我们本可以更有信心。所以如果我们说我们 100%有信心,损失将为零。
acts = np.array([1, 0, 0, 1])
preds = np.array([0.9, 0.1, 0.2, 0.8])
binary_loss(acts, preds)
'''
0.164252033486018
'''
所以让我们在 Excel 中看一下。从顶部行开始:
-
我们的预测
-
实际/目标值
-
1 减去实际/目标值
-
我们的预测的对数
-
我们的预测的对数的 1 减
-
总和

如果你仔细想一想,我希望你在这一周内考虑一下,你可以用一个 if 语句来替换这个(np.mean(-(y * np.log(p) + (1-y)*np.log(1-p)))),而不是 y,因为 y 总是 1 或 0,所以它只会使用np.log(p)或(np.log(1-p)中的一个。所以你可以用一个 if 语句来替换这个。所以我希望你在这一周内尝试用一个 if 语句来重写这个。
然后看看你是否能将其扩展为分类交叉熵。所以分类交叉熵的工作方式是这样的。假设我们试图预测 3、6、7、2。
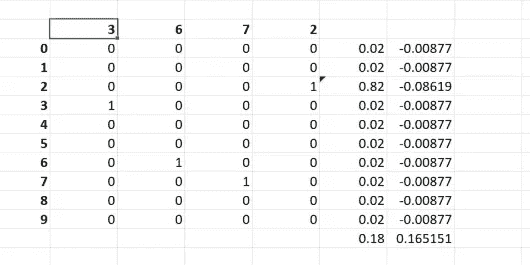
所以如果我们试图预测 3,而实际上预测了 5,或者试图预测 3,却意外地预测了 9。5 而不是 3 并不比 9 而不是 3 更好。所以我们实际上不会说实际数字有多远。我们会用不同的方式表达它。换句话说,如果我们试图预测猫、狗、马和飞机。猫和马之间有多远?所以我们会稍微不同地表达这些。与其把它看作是一个 3,不如把它看作是一个在第三个位置上有一个 1 的向量:

不要把它看作是一个 6,让我们把它看作是一个零向量,第 6 个位置是 1。换句话说,独热编码。所以让我们对我们的因变量进行独热编码。这样现在,我们不再试图预测一个数字,而是预测十个数字。让我们预测它是 0 的概率,它是 1 的概率,依此类推。

所以让我们假设我们正在预测 2,这里是我们的分类交叉熵[1:07:50]。所以它只是在说,这个预测是否正确,有多大偏差,依此类推,对每一个进行计算,然后将它们全部加起来。分类交叉熵与二元交叉熵是相同的。我们只需要将它们加起来跨越所有的类别。
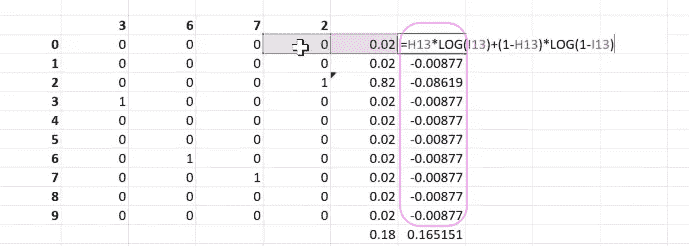
所以尝试将 Python 中的二元交叉熵函数转换为 Python 中的分类交叉熵。也许创建带有 if 语句的版本和带有求和和乘积的版本。
这就是为什么在我们的 PyTorch 中,我们将这个矩阵的输出维度设置为 10,因为当我们将一个有 10 列的矩阵相乘时,我们将得到一个长度为 10 的结果,这正是我们想要的[1:08:35]。我们想要有 10 个预测。
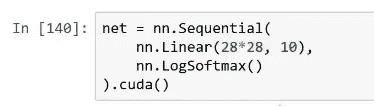
这就是我们正在使用的损失函数。然后我们可以拟合模型,它会遍历每个图像,这么多次(epochs)。所以在这种情况下,它只是查看每个图像一次,并且会根据这些梯度稍微更新那个权重矩阵中的值。
所以一旦我们训练好了,我们就可以用这个模型(net)在验证集(md.val_dl)上进行predict。
preds = predict(net, md.val_dl)
现在这会输出一个 10,000 乘以 10 的东西。我们有 10,000 张图像进行验证,实际上每张图像进行 10 次预测。换句话说,每一行都是它是 0 的概率,它是 1 的概率,它是 2 的概率,依此类推。
preds.shape
'''
(10000, 10)
'''
Argmax [1:10:22]
在数学中,有一个我们经常做的操作叫做argmax。当我说它很常见时,很有趣的是在高中,我从来没有见过 argmax。大一,我也从来没有见过 argmax。但不知何故,大学毕业后,一切都与 argmax 有关。所以有些事情在学校里似乎并没有真正教,但实际上它非常关键。argmax 既是数学中的一个东西(它只是完整地写出argmax),它在 numpy 中,在 PyTorch 中,非常重要。它的作用是让我们拿这些预测数组,然后在给定的轴上(axis=1 - 记住,轴 1 是列),就像 Chis 所说的,对于每一行的 10 个预测,让我们找出哪个预测值最高,然后返回不是那个值(如果只是说 max,它会返回值),argmax 返回值的索引。所以通过说argmax(axis=1),它将返回实际上是数字本身的索引。所以让我们取前 5 个:
preds.argmax(axis=1)[:5]
'''
array([3, 8, 6, 9, 6])
'''
这就是我们如何将我们的概率转换回预测的方法。我们保存下来并称之为preds。然后我们可以说preds何时等于真实值。这将返回一个布尔数组,我们可以将其视为 1 和 0,一堆 1 和 0 的平均值就是平均值。这给了我们 91.8%的准确率。
preds = preds.argmax(1)
np.mean(preds == y_valid)
'''
0.91820000000000002
'''
所以你想要能够复制你看到的数字,这里就是。这里是我们的 91.8%。
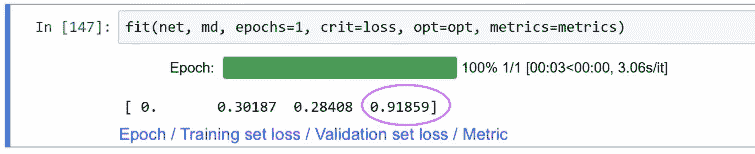
所以当我们训练这个模型时,最后一件事告诉我们的是我们要求的任何指标,我们要求的是准确率。然后在此之前,我们得到了训练集的损失。损失又是我们要求的任何损失(nn.NLLLoss()),第二件事是验证集的损失。PyTorch 不使用损失这个词,他们使用准则这个词。所以你会在这里看到crit,这就是准则等于损失。这就是我们想要使用的损失函数,他们称之为准则。同样的事情。所以np.mean(preds == y_valid)就是我们如何重新创建准确率的方法。
plots(x_imgs[:8], titles=preds[:8])

因此,现在我们可以继续绘制八幅图像以及它们的预测。对于我们预测错误的那些,您可以看到它们为什么错误。数字 4 的图像非常接近数字 9。它只是在顶部少了一个小交叉。数字 3 非常接近数字 5。它在顶部有一点额外的部分。所以我们已经开始了。到目前为止,我们实际上还没有创建一个深度神经网络。我们实际上只有一个层。因此,我们实际上所做的是创建了一个逻辑回归。逻辑回归就是我们刚刚构建的内容,您可以尝试使用 sklearn 的逻辑回归包来复制这个过程。当我这样做时,我得到了类似的准确性,但这个版本运行得更快,因为它在 GPU 上运行,而 sklearn 在 CPU 上运行。因此,即使对于像逻辑回归这样的东西,我们也可以使用 PyTorch 非常快速地实现它。
问题:当我们创建我们的网络时,我们必须执行.cuda()。如果不这样做会有什么后果?它只是不会快速运行。它将在 CPU 上运行。
问题:为什么我们必须先进行线性操作,然后再进行非线性操作?简短的答案是因为这是通用逼近定理所说的结构,可以为任何函数形式提供任意精确的函数。长答案是通用逼近定理为何有效的细节。另一个简短答案是,这就是神经网络的定义。因此,神经网络的定义是一个线性层,后跟一个激活函数,再后跟一个线性层,再后跟一个激活函数,依此类推。我们在深度学习课程中会更详细地讨论这一点,但就此目的而言,知道它有效就足够了。到目前为止,当然,我们实际上还没有构建一个深度神经网络。我们只是构建了一个逻辑回归。因此,在这一点上,如果你考虑一下,我们所做的就是将每个输入像素乘以每个可能结果的权重。因此,我们基本上是在说,平均而言,数字 1 具有这些像素点亮。数字 2 具有这些像素点亮。这就是为什么它不是非常准确的原因。这不是现实生活中数字识别的工作方式。但到目前为止,这就是我们构建的全部内容。
问题:所以你一直在说这个通用逼近定理。你有定义过吗?是的,但让我们再次讨论一下,因为这值得谈论。因此,Michael Nielsen 有一个名为神经网络与深度学习的优秀网站。他的第四章现在实际上很有名,其中他通过演示神经网络可以以足够大的规模逼近任何其他函数,只要它足够大,来详细介绍这一点。我们在深度学习课程中详细讨论了这一点,但基本的诀窍是,他展示了通过几个不同的数字,您基本上可以使这些事物创建小盒子,您可以将盒子上下移动,您可以将它们移动,您可以将它们连接在一起,最终基本上可以创建像塔一样的连接,您可以用来逼近任何类型的表面。


因此,这基本上就是诀窍。因此,我们所需要做的就是,鉴于此,找到神经网络中每个线性函数的参数。因此,找到每个矩阵中的权重。到目前为止,我们只有一个矩阵,我们只是构建了一个简单的逻辑回归。
问题:我只是想确认一下,当你展示被错误分类的图像的例子时,它们看起来是矩形的,所以只是在渲染时,像素被不同地缩放了吗?它们是 28 乘 28 的。我认为它们看起来是矩形的,因为它们顶部有标题。Matplotlib 经常会调整它认为的黑色与白色以及具有不同大小轴等的东西。因此,有时你必须小心一点。
自己定义逻辑回归
希望现在这会更有意义,因为我们要深入一层,定义逻辑回归,而不使用nn.Sequential、nn.Linear或nn.LogSoftmax。因此,我们将几乎所有的层定义都从头开始做。为了做到这一点,我们将不得不定义一个 PyTorch 模块。PyTorch 模块基本上是一个神经网络或神经网络中的一层,这实际上是一个强大的概念。基本上,任何可以像神经网络一样行为的东西本身可以成为另一个神经网络的一部分。这就是我们如何构建特别强大的架构,结合了许多其他部分。
def get_weights(*dims):
return nn.Parameter(torch.randn(dims)/dims[0])
def softmax(x):
return torch.exp(x)/(torch.exp(x).sum(dim=1)[:,None])
class LogReg(nn.Module):
def __init__(self):
super().__init__()
self.l1_w = get_weights(28*28, 10) # Layer 1 weights
self.l1_b = get_weights(10) # Layer 1 bias
def forward(self, x):
x = x.view(x.size(0), -1)
x = (x @ self.l1_w) + self.l1_b # Linear Layer
x = torch.log(softmax(x)) # Non-linear (LogSoftmax) Layer
return x
因此,要创建一个 PyTorch 模块,只需创建一个 Python 类,但它必须继承自nn.Module。因此,除了继承之外,这是我们已经在面向对象中看到的所有概念。基本上,如果你在这里(在类名后面)放入括号中的内容,意味着我们的类会免费获得这个类的所有功能。这被称为子类化。因此,我们将获得 PyTorch 作者提供的神经网络模块的所有功能,然后我们将添加额外的功能。当你创建一个子类时,有一件重要的事情你需要记住,那就是当你初始化你的类时,你首先必须初始化超类。因此,超类是nn.Module。因此,在你开始添加你的部分之前,必须先构建nn.Module。这就像你可以复制并粘贴到你的每一个模块中的东西。你只需说super().__init__()。这意味着首先构造超类。
这样做之后,我们现在可以定义我们的权重和偏差。我们的权重是权重矩阵。这是我们将要用来乘以我们的数据的实际矩阵。正如我们讨论过的,它将有 28 乘 28 行和 10 列。这是因为如果我们取一个我们已经展平成一个 28 乘 28 长度向量的图像,然后我们可以将它乘以这个权重矩阵,得到一个长度为 10 的向量,然后我们可以将其视为一组预测。这就是我们的权重矩阵。现在问题是我们不只是想要y = ax。我们想要y = ax + b。因此,在神经网络中,+ b被称为偏差。因此,除了定义权重,我们还将定义偏差。由于这个get_weights(28*28, 10)将为每个图像输出长度为 10 的东西。这意味着我们需要创建一个长度为 10 的向量作为我们的偏差。换句话说,对于每个 0、1、2、3 直到 9,我们将有一个不同的加b。因此,我们有我们的数据矩阵,它的长度是 10,000 乘以 28 乘以 28。然后我们有我们的权重矩阵,它是 28 乘以 28 乘以 10。因此,如果我们将它们相乘,我们将得到一个大小为 10,000 乘以 10 的东西。

然后我们想要添加我们的偏差,如下所示:

我们以后会学到更多关于这个的知识,但是当我们像这样添加一个向量时,基本上它会被添加到每一行。因此,那个偏差将被添加到每一行。因此,我们首先定义这些。为了定义它们,我们创建了一个名为get_weights的小函数,它基本上只是创建一些正态分布的随机数。torch.randn返回一个填充有正态分布随机数的张量。

然而,我们必须要小心。当我们进行深度学习时,比如以后添加更多的线性层。想象一下,如果我们有一个矩阵,平均倾向于增加我们输入的大小。如果我们将其乘以许多相同大小的矩阵,它会使数字变得越来越大,指数级增长。或者如果我们让它们变小一点呢?它会使它们变得越来越小,指数级减小。因为深度网络应用了许多线性层,如果平均而言它们导致的结果比起始值稍微大一点或稍微小一点,那么它将指数级地放大这种差异。因此,我们需要确保权重矩阵的大小适当,使得输入到它的(更具体地说,输入的均值)不会改变。
事实证明,如果你使用正态分布的随机数并除以权重矩阵中的行数,这种随机初始化可以保持你的数字在大约正确的范围内。因此,这个想法是,如果你做过线性代数,基本上如果第一个特征值大于 1 或小于 1,它会导致梯度变得越来越大或越来越小。这就是梯度爆炸。我们将在深度学习课程中更多地讨论这个问题,但如果你感兴趣,你可以查看Kaiming He 初始化,并阅读有关这个概念的所有内容,但现在,知道如果你使用这种类型的随机数生成(即torch.randn(dims)/dims[0]),你将得到行为良好的随机数。你将从均值为 0 标准差为 1 的输入开始。一旦你通过这组随机数,你仍然会得到大约均值为 0 标准差为 1 的东西。这基本上就是目标。
PyTorch 的一个好处是你可以玩弄这些东西[1:25:44]。所以试一试。每当你看到一个函数被使用时,运行它并查看一下。所以你会发现,它看起来很像 numpy,但它不返回一个 numpy 数组。它返回一个张量。

事实上,现在我在进行 GPU 编程。

调用.cuda(),现在它在 GPU 上运行。

我在 GPU 上非常快地将那个矩阵乘以 3!这就是我们如何使用 PyTorch 进行 GPU 编程。
正如我们所说,我们创建了一个 28*28 乘以 10 的权重矩阵,另一个只是 10 的秩 1 偏差[1:26:29]。我们必须将它们设为参数。这基本上告诉 PyTorch 在执行 SGD 时要更新哪些内容。这是一个非常微小的技术细节。

创建了权重矩阵后,我们定义了一个名为forward的特殊方法。这是一个特殊的方法,而在 PyTorch 中,名称 forward 具有特殊含义。在 PyTorch 中,称为 forward 的方法是在计算层时将被调用的方法名称。因此,如果你创建了一个神经网络或一个层,你必须定义 forward,它将传递前一层的数据。我们的定义是对输入数据和权重进行矩阵乘法,并加上偏差。就是这样。这就是我们之前说的nn.Linear时发生的事情。它为我们创建了这个东西。
不幸的是,我们并没有得到一个 28 乘以 28 的长向量。我们得到的是一个 28 行乘以 28 列的矩阵,所以我们必须将其展平。不幸的是,在 PyTorch 中,它们倾向于重新命名事物。他们将“resize”拼写为view。所以view意味着重塑。因此,你可以看到这里x.view(x.size(0), -1),我们最终得到的是一个图像数量(x.size(0))不变。然后我们将行替换为列,形成一个单一轴。再次,-1的意思是尽可能长。这就是我们使用 PyTorch 展平的方法。
所以我们将其展平,进行矩阵乘法,最后进行 softmax。所以 softmax 是我们使用的激活函数。如果您查看深度学习存储库,您会发现一个名为熵示例的内容,您将在其中看到 softmax 的示例。Softmax 简单地获取我们最终层的输出,因此我们从线性层获取输出。我们所做的是对每个输出进行e的(e^)运算。

然后我们取这个数字,除以e的幂的总和。

这就是所谓的 softmax。为什么我们这样做?因为我们正在将这个(exp)除以总和,这意味着这些本身的总和必须加起来为一。这就是我们想要的。我们希望所有可能结果的概率总和为一。此外,因为我们使用e^,这意味着我们知道这些(softmax)中的每一个都在零和一之间。我们知道概率将在零和一之间。最后,因为我们使用e的幂,这意味着输入中稍大的值会变成输出中的更大值。因此,通常情况下,您会看到我的 softmax 中有一个大数和许多小数。这就是我们想要的,因为我们知道输出是一热编码的。换句话说,softmax 激活函数,softmax 非线性,是一种返回类似概率的东西的东西,其中其中一个概率更有可能是高的,其他概率更有可能是低的。我们知道这就是我们想要映射到我们的一热编码的内容,因此 softmax 是一个很好的激活函数,可以帮助神经网络更容易地映射到您想要的输出。这通常是我们想要的。当我们设计神经网络时,我们尝试提出一些小的架构调整,使其尽可能容易地匹配我们想要的输出。
这基本上就是这样。与其使用 Sequential 和nn.Linear以及nn.LogSoftmax,我们从头开始定义了它。现在我们可以说,就像以前一样,我们的net2等于LogReg().cuda(),我们可以说fit,我们得到了几乎完全相同的输出,只是有轻微的随机偏差。
net2 = LogReg().cuda()
opt=optim.Adam(net2.parameters())
fit(net2, md, n_epochs=1, crit=loss, opt=opt, metrics=metrics)
'''
[ 0\. 0.32209 0.28399 0.92088]
'''
所以我希望你在这一周里尝试使用torch.randn生成一些随机张量,使用torch.matmul开始将它们相乘,相加,尝试确保你可以自己从头开始重写 softmax。尝试玩弄一下重塑、view 等等,这样到下周你回来时就会感觉对 PyTorch 相当舒适。
如果您搜索 PyTorch 教程,您会看到PyTorch 网站上有很多很好的材料可以帮助您,向您展示如何创建张量,修改它们以及对它们进行操作。
问题:我看到前向是在每个线性层之后应用的层。
Jeremy:不完全是。前向只是模块的定义,这是我们实现 Linear 的方式。
继续:这是否意味着在每个线性层之后,您必须应用相同的函数?假设我们不能在第一层之后应用 LogSoftmax,然后在第二层之后应用其他函数,如果我们有一个多层神经网络?
Jeremy:所以通常我们这样定义神经网络:

我们只是说这里是我们想要的层的列表。您不必编写自己的前向。我们刚刚做的是说,与其这样做,不如完全不使用这些,而是自己手写所有内容。因此,您可以按任何顺序编写任意数量的层。重点是在这里,我们没有使用任何这些:

我们已经编写了自己的matmul加偏置项,自己的 softmax,所以这只是 Python 代码。您可以在 forward 函数内编写任何您喜欢的 Python 代码来定义自己的神经网络。通常情况下,您不会自己这样做。通常您只会使用 PyTorch 提供的层,并使用.Sequential将它们组合在一起。或者更有可能的是,您会下载一个预定义的架构并使用它。我们只是为了学习它在幕后是如何工作的。
好的,太棒了。谢谢大家!
机器学习 1:第 9 课
原文:
medium.com/@hiromi_suenaga/machine-learning-1-lesson-9-689bbc828fd2译者:飞龙
协议:CC BY-NC-SA 4.0
来自机器学习课程的个人笔记。随着我继续复习课程以“真正”理解它,这些笔记将继续更新和改进。非常感谢 Jeremy 和 Rachel 给了我这个学习的机会。
学生的作品[0:00]
欢迎回到机器学习!我非常兴奋能够分享一些由旧金山大学学生在这一周内构建或撰写的惊人内容。我将向你展示的许多东西已经在互联网上广泛传播:大量的推文和帖子以及各种各样的事情发生。
用随机森林着色
由Tyler White提供
他开始说,如果我创建一个合成数据集,其中自变量是 x 和 y,因变量是颜色,会怎样。有趣的是,他向我展示了一个早期版本,那时他没有使用颜色。他只是把实际的数字放在这里。

这个东西一开始根本不起作用。一旦他开始使用颜色,它就开始运行得非常好。所以我想提一下,不幸的是我们在 USF 没有教给你的一件事是人类感知的理论,也许我们应该。因为实际上,当涉及到可视化时,最重要的事情是了解人眼或大脑擅长感知的是什么。关于这个有一个整个学术研究领域。我们最擅长感知的事情之一就是颜色的差异。这就是为什么当我们看这张他创建的合成数据的图片时,你可以立刻看到,哦,这里有四个较浅红色的区域。他所做的是,他说好,如果我们尝试创建一个关于这个合成数据集的机器学习模型,具体来说他创建了一棵树。而酷的事情是你实际上可以绘制这棵树。所以在他创建了这棵树之后,他在 matplotlib 中完成了所有这些。Matplotlib 非常灵活。他实际上绘制了树的边界,这已经是一个相当不错的技巧——能够实际绘制这棵树。

然后他做了更聪明的事情,他说好的,那么树做出了什么预测?嗯,这是每个区域的平均值,所以为了做到这一点,我们实际上可以绘制平均颜色。这实际上相当漂亮。这是树所做的预测。现在这里变得非常有趣。你可以,如你所知,通过重新采样随机生成树,所以这里有通过重新采样生成的四棵树。它们都非常相似但略有不同。

现在我们实际上可以可视化装袋,为了可视化装袋,我们简单地取四张图片的平均值。这就是装袋。就是这样:

这是一个随机森林的模糊决策边界,我觉得这很神奇。因为这就像,我真希望在我开始教你们随机森林的时候有这个,我本来可以跳过几节课的。就像“好的,这就是我们做的”。我们创建决策边界,对每个区域进行平均,然后重复几次并对所有结果进行平均。这就是随机森林的做法,我认为这只是一个通过图片将复杂问题变得简单的很好的例子。所以恭喜 Tyler。事实上,他实际上重新发明了别人已经做过的事情。一个叫 Christian Innie(?)的人,他后来成为了世界上最重要的机器学习研究者之一,实际上在他写的一本关于决策森林的书中几乎完全包含了这个技术。所以 Tyler 最终重新发明了一个世界上最重要的决策森林专家创造的东西,这实际上很酷。我觉得这很有趣。很好,因为当我们在 Twitter 上发布这个时,引起了很多关注,最终有人能够说“哦,你知道吗,这实际上已经存在了”。所以 Tyler 已经开始阅读那本书。
Parfit - 快速而强大的超参数优化与可视化 [4:16]
由 Jason Carpenter
另一件很酷的事情是 Jason Carpenter 创建了一个全新的库叫做 Parfit。Parfit 是为了选择超参数而并行拟合多个模型。我真的很喜欢这个。他展示了如何使用它的清晰示例,API 看起来非常类似于其他基于网格搜索的方法,但它使用了 Rachel 写的验证技术,我们几周前学到的使用一个好的验证集。他在介绍它的博客文章中,回顾了什么是超参数,为什么我们必须训练它们,并解释了每一步。然后这个模块本身非常完善。他为其添加了文档,为其添加了一个很好的 README。当你实际看代码时,你会发现它非常简单,这绝对不是坏事,简单是好事。通过编写这段代码并将其打包得如此完美,他使其他人使用这个技术变得非常容易,这很棒。
如何使用 parfit 使 SGD 分类器表现得和逻辑回归一样好 [5:40]
由Vinay Patlolla
我真的很高兴看到的一件事是 Vinay 继续结合了我们课堂上学到的两件事:一是使用 Parfit,另一是使用我们在上一课中学到的加速 SGD 分类方法,将两者结合起来,说“好的,现在让我们使用 Parfit 来帮助我们找到 SGD 逻辑回归的参数”。我认为这真的是一个很好的主意。
随机森林的直观解释 [6:14]
由 Prince Grover
我认为很棒的另一件事是,Prince 基本上总结了我们在随机森林解释中学到的几乎所有内容。他甚至比那更进一步,因为他描述了随机森林解释的每种不同方法。他描述了如何做到这一点,例如,通过变量置换来计算特征重要性,每个方法都有一个小图片,然后非常酷,这里是从头开始实现它的代码。我认为这是一篇非常好的文章,描述了很多人不理解的东西,并且准确展示了它是如何工作的,既有图片又有实现代码。所以我认为这真的很棒。我在这里真的很喜欢的一件事是,对于树解释器,他实际上展示了如何将树解释器的输出输入到由 USF 学生 Chris 构建的新瀑布图包中,以展示如何实际上在瀑布图中可视化树解释器的贡献。所以再次,这是一种很好的结合我们学习和作为一个团队构建的多种技术。
Keras Model for Beginners (0.210 on LB)+EDA+R&D [7:37]
由Davesh Maheshwari提供
有一些有趣的内核分享,下周我会分享更多,Davesh 写了这篇非常好的内核,展示了在检测冰山与船只的 Kaggle 竞赛中的挑战。这是一种很难可视化的奇怪的双通道卫星数据,他实际上通过并基本上描述了这些雷达散射的工作原理的公式,然后实际上设法编写了一个代码,使他能够重新创建实际的 3D 冰山或船只。我以前没有见过这样做。如何可视化这些数据是非常具有挑战性的。然后他继续展示如何构建神经网络来尝试解释这一点,这也非常棒。
SGD [9:53]
笔记本
让我们回到 SGD。所以我们正在回顾这份笔记本,Rachel 基本上带领我们从头开始学习 SGD,目的是进行数字识别。实际上,今天我们看的很多东西都将紧随计算线性代数课程的一部分,你可以在 fast.ai 上找到MOOCs,或者在 USF,它将成为明年的选修课。所以如果你觉得这些东西有趣,我希望你会考虑报名参加选修课或在线观看视频。
所以我们正在构建神经网络。我们假设已经下载了 MNIST 数据,通过减去平均值并除以标准差对其进行了标准化。这些数据略有不同,虽然它们代表图像,但它们被下载为每个图像都是 784 个长的秩为 1 的张量,因此已经被展平。为了绘制它的图片,我们必须将其调整为 28x28。但实际的数据不是 28x28,而是 784 个长的展平数据。
我们要采取的基本步骤是从训练世界上最简单的神经网络开始,基本上是一个逻辑回归。因此没有隐藏层。我们将使用一个名为 Fast AI 的库进行训练,并使用一个名为 PyTorch 的库构建网络。然后我们将逐渐摆脱所有库。首先,我们将摆脱 PyTorch 中的nn(神经网络)库,并自己编写。然后我们将摆脱 Fast AI 的fit函数,并自己编写。然后我们将摆脱 PyTorch 的优化器,并自己编写。因此,在本笔记本的最后,我们将自己编写所有部分。我们最终依赖的唯一两个 PyTorch 给我们的关键事物是:
-
具有编写 Python 代码并在 GPU 上运行的能力
-
具有编写 Python 代码并使其自动为我们进行微分的能力。
因此,这两件事我们不打算自己尝试编写,因为这很无聊且毫无意义。但除此之外,我们将尝试在这两件事的基础上自己编写其他所有内容。
我们的起点不是自己做任何事情。基本上所有事情都已经为我们完成。因此,PyTorch 有一个nn库,其中包含神经网络的内容。您可以通过使用Sequential函数创建一个多层神经网络,然后传入您想要的层的列表,我们要求一个线性层,然后是一个 softmax 层,这定义了我们的逻辑回归。
from fastai.metrics import *
from fastai.model import *
from fastai.dataset import *
import torch.nn as nnnet = nn.Sequential(
nn.Linear(28*28, 10),
nn.LogSoftmax()
).cuda()
我们线性层的输入是 28 乘以 28,输出是 10,因为我们希望为我们的图像中的每个数字 0 到 9 之间的每个数字获得一个概率。.cuda()将其放在 GPU 上,然后fit拟合模型。
loss=nn.NLLLoss()
metrics=[accuracy]
opt=optim.Adam(net.parameters())
fit(net, md, n_epochs=5, crit=loss, opt=opt, metrics=metrics)
因此,我们从一组随机权重开始,然后使用梯度下降进行拟合以使其更好。我们必须告诉拟合函数要使用什么标准,换句话说,什么算作更好,我们告诉它使用负对数似然。我们将在下一课中了解这是什么。我们必须告诉它要使用什么优化器,我们说请使用optim.Adam,这方面的细节我们在本课程中不会涉及。我们将构建一个更简单的称为 SGD 的东西。如果您对 Adam 感兴趣,我们刚刚在深度学习课程中涵盖了这一点。您想要打印出什么指标,我们决定打印出准确率。就是这样。所以在我们拟合后,我们通常会得到大约 91、92%的准确率。
定义模块
接下来我们要做的是,我们将重复这完全相同的事情,所以我们将重建这个模型 4 到 5 次,逐渐减少使用的库。我们上次做的第二件事是尝试开始自己定义模块。所以我们不再使用那个库,而是尝试从头开始自己定义它。为了做到这一点,我们必须使用面向对象,因为这是我们在 PyTorch 中构建所有东西的方式。我们必须创建一个类,该类继承自nn.Module。所以nn.Module是一个 PyTorch 类,它接受我们的类并将其转换为神经网络模块,这基本上意味着您从nn.Module继承的任何东西,您几乎可以将其插入到神经网络中作为一个层,或者您可以将其视为一个神经网络。它将自动获得作为神经网络的一部分或整个神经网络运行所需的所有内容。现在我们将在今天和下一课中详细讨论这意味着什么。
因此我们需要构建这个对象,这意味着我们需要定义构造函数 dunder init。重要的是,这是一个 Python 的东西,如果你继承自其他对象,那么你首先必须创建你继承的东西。因此当你说super().__init__()时,这意味着首先构建那个nn.Module部分。如果你不这样做,那么nn.Module的东西就永远没有机会被实际构建。因此这就像一个标准的 Python 面向对象子类构造函数。如果其中有任何地方让你感到困惑,那么你知道这就是你绝对需要抓住一个 Python 面向对象的入门,因为这是标准的方法。
def get_weights(*dims):
return nn.Parameter(torch.randn(dims)/dims[0])
def softmax(x):
return torch.exp(x)/(torch.exp(x).sum(dim=1)[:,None])
class LogReg(nn.Module):
def __init__(self):
super().__init__()
self.l1_w = get_weights(28*28, 10) # Layer 1 weights
self.l1_b = get_weights(10) # Layer 1 bias
def forward(self, x):
x = x.view(x.size(0), -1)
x = (x @ self.l1_w) + self.l1_b # Linear Layer
x = torch.log(softmax(x)) # Non-linear (LogSoftmax) Layer
return x
因此,在我们的构造函数中,我们想要做的相当于nn.Linear。nn.Linear所做的是,它将我们的 28 乘以 28 的向量,即 784 个元素的向量,作为矩阵乘法的输入。因此,现在我们需要创建一个具有 784 行和 10 列的矩阵。因为这个的输入将是一个大小为 64 乘以 784 的小批量数据。因此我们将进行这个矩阵乘法运算。因此当我们在 PyTorch 中说nn.Linear时,它将为我们构建一个 784 乘以 10 的矩阵。因此,由于我们没有使用它,我们是从头开始做事情,我们需要自己制作它。为了自己制作它,我们可以说生成具有这种维度的正态随机数torch.randn(dims),我们在这里传入了28*28, 10。这样我们就得到了我们随机初始化的矩阵。
然后我们想要添加到这个。我们不只是想要 y = ax,我们想要 y = ax + b。所以我们需要添加在神经网络中称为偏置向量的东西。因此,我们在这里创建一个长度为 10 的偏置向量 self.l1_b = get_weights(10),同样是随机初始化的,所以现在我们有了两个随机初始化的权重张量。

这就是我们的构造函数。现在我们需要定义前向传播。为什么我们需要定义前向传播?这是一个 PyTorch 特有的东西。当你在 PyTorch 中创建一个模块时,你得到的对象会表现得好像它是一个函数。你可以用括号调用它,我们马上就会这样做。因此,你需要以某种方式定义当你调用它时会发生什么,就好像它是一个函数,答案是 PyTorch 调用一个叫做 forward 的方法。这是他们选择的 PyTorch 方法。所以当它调用 forward 时,我们需要做这个模块或层的输出的实际计算。这就是在逻辑回归中实际计算的东西。基本上我们取得我们的输入 x,它被传递给 forward —— 这基本上是 forward 的工作原理,它接收到小批量数据,并且我们将其与构造函数中定义的第一层权重进行矩阵乘法运算。然后我们加上构造函数中也定义的第一层偏置。实际上,现在我们可以更加优雅地使用 Python 3 的矩阵乘法运算符@来定义这个。

当你使用它时,我认为你最终会得到更接近数学符号的样子,所以我觉得这更好看。
好了,这就是我们逻辑回归中的线性层(即我们的零隐藏层神经网络)。然后我们对其进行 softmax。我们得到这个矩阵乘法的输出,它的维度是 64 乘以 10。我们得到这个输出矩阵,然后我们通过 softmax 函数处理它。为什么我们要通过 softmax 函数处理它?我们要通过 softmax 函数处理它是因为最终,对于每个图像,我们希望得到一个概率,它是 0、1、2、3 或 4。所以我们希望得到一堆概率,它们加起来等于 1,其中每个概率都在 0 到 1 之间。所以 softmax 函数正好为我们做到了这一点。
例如,如果我们不是从零到 10 中挑选数字,而是挑选猫、狗、飞机、鱼或建筑物,那么一个特定图像的矩阵乘积的输出可能看起来像这样(输出列)。这些只是一些随机数。为了将其转换为 softmax,我首先对这些数字中的每一个进行e的幂运算。我将这些e的幂相加。然后我将这些e的幂中的每一个除以总和。这就是 softmax。这就是 softmax 的定义。

因为它是e的幂,这意味着它始终是正的。因为它被总和除以,这意味着它始终在 0 和 1 之间,并且还意味着它们总是加起来等于 1。因此,通过应用这个 softmax 激活函数,每当我们有一层输出,我们称之为激活,然后我们对其应用一些非线性函数,将一个标量映射到一个标量,比如 softmax(我们称之为激活函数)。因此,softmax 激活函数将我们的输出转换为类似概率的东西。严格来说,我们不需要它。我们仍然可以尝试训练直接输出概率的东西。但是通过使用这个函数,它自动使它们始终表现得像概率,这意味着网络需要学习的内容更少,因此它会学得更好。因此,一般来说,每当我们设计一个架构时,我们都会尽可能地设计它,以便它尽可能地创建我们想要的形式。这就是为什么我们使用 softmax 的原因。
这就是基本步骤。我们有我们的输入,它是一堆图像,它被一个权重矩阵相乘,我们还添加一个偏置以获得线性函数的输出。我们将其通过一个非线性激活函数,这种情况下是 softmax,这给我们带来了我们的概率。
所以这就是全部。PyTorch 也倾向于使用 softmax 的对数,原因并不需要现在困扰我们。基本上是为了数值稳定性的便利。因此,为了使这与我们在上面看到的nn.LogSoftmax()版本相同,我也将在这里使用对数。好的,现在我们可以实例化这个类(即创建这个类的对象)。

问题:我有一个关于之前的概率的问题。如果我们有一张照片上有一只猫和一只狗,那会改变它的工作方式吗?或者它的基本工作方式是一样的。这是一个很好的问题。所以如果你有一张照片上有一只猫和一只狗,你希望它同时输出猫和狗,这将是一个非常糟糕的选择。Softmax 是我们专门用于分类预测的激活函数,我们只想预测其中一种东西。因此,部分原因是因为正如你所看到的,因为我们使用e的幂,稍微更大的e会产生更大的数字。因此,通常我们只有一两个大的东西,其他东西都很小。因此,如果我重新计算这些随机数(在 Excel 表中),你会看到它往往是一堆零和一两个高数字。因此,它真的是设计成试图让预测这一件事变得容易。如果你正在进行多标签预测,所以我只想找到这张图片中的所有东西,而不是使用 softmax,我们将使用 sigmoid。Sigmoid 会导致这些东西中的每一个都在 0 和 1 之间,但它们不再加起来等于 1。

关于最佳实践的许多细节是我们在深度学习课程中涵盖的内容,我们在机器学习课程中不会涵盖大量这些内容。我们更感兴趣的是机制。但是如果它们很快,我们会尝试涵盖它们。
现在我们已经得到了这个,我们可以实例化该类的一个对象[27:30]。当然我们想将其复制到 GPU 上。这样我们可以在那里进行计算。再次,我们需要一个优化器,我们很快会讨论这是什么。但你看到这里,我们在我们的类上调用了一个名为parameters的函数。但我们从未定义过一个叫做 parameters 的方法,这将会起作用的原因是因为它实际上是在nn.Module内部为我们定义的。所以nn.Module会自动遍历我们创建的属性,并找到任何我们说这是一个参数的东西。你说某个东西是参数的方式是将它包装在nn.Parameter中。这只是告诉 PyTorch 这是我想要优化的东西的方式。所以当我们创建权重矩阵时,我们只是用nn.Parameter包装它,这与我们很快要学习的常规 PyTorch 变量完全相同。这只是一个小标志,告诉 PyTorch 你应该优化这个。所以当你在我们创建的net2对象上调用net2.parameters()时,它会遍历我们在构造函数中创建的所有东西,检查是否有任何一个是Parameter类型,如果是,它会将所有这些东西设置为我们要用优化器训练的东西。我们稍后将从头开始实现优化器。
net2 = LogReg().cuda()
opt=optim.Adam(net2.parameters())
做完这些,我们可以拟合[28:51]。我们应该基本上得到与之前相同的答案(即 91 左右)。看起来不错。
fit(net2, md, n_epochs=1, crit=loss, opt=opt, metrics=metrics)
数据加载器[29:05]
那么我们实际上在这里构建了什么?嗯,正如我所说的,我们实际上构建的是可以像常规函数一样运行的东西。所以我想向你展示如何实际上将其作为一个函数调用。为了能够将其作为一个函数调用,我们需要能够向其传递数据。为了能够向其传递数据,我需要获取一个 MNIST 图像的小批量。为了方便起见,我们使用了 Fast AI 的ImageClassifierData.from_arrays方法,它会为我们创建一个 PyTorch DataLoader。PyTorch DataLoader 是一种获取几张图像并将它们放入一个小批量并使其可用的东西。你基本上可以说给我另一个小批量,给我另一个小批量,给我另一个小批量。所以在 Python 中,我们称这些东西为生成器。生成器是一种东西,你基本上可以说我想要另一个,我想要另一个,我想要另一个。迭代器和生成器之间有非常紧密的联系,我现在不打算担心它们之间的区别。但你会看到,为了获得我们可以说请给我另一个的东西,为了获取我们可以用来生成小批量的东西,我们必须取出我们的数据加载器,这样你就可以从我们的模型数据对象中请求训练数据。你会看到有很多不同的数据加载器可以请求:测试数据加载器、训练数据加载器、验证数据加载器、增强图像数据加载器等等。
dl = iter(md.trn_dl)
所以我们要获取为我们创建的训练数据加载器。这是一个标准的 PyTorch 数据加载器,稍微被我们优化了一下,但是思路是一样的。然后你可以说这个(iter)是一个标准的 Python 东西,我们可以说将其转换为一个迭代器,即我们可以一次从中获取另一个的东西。一旦你这样做了,我们就有了一个可以迭代的东西。你可以使用标准的 Python next函数从生成器中获取一个更多的东西。
xmb,ymb = next(dl)
所以这是从一个小批量返回 x 和 y。在 Python 中,您可以使用for循环来使用生成器和迭代器。我也可以说 x 小批量逗号 y 小批量在数据加载器中,然后做一些事情:

所以当你这样做时,实际上是在幕后,它基本上是调用next很多次的语法糖。所以这都是标准的 Python 东西。
所以它返回了一个大小为 64 乘以 784 的张量,这是我们所期望的。我们使用的 Fast AI 库默认使用小批量大小为 64,这就是为什么它这么长。这些都是背景零像素,但它们实际上并不是零。在这种情况下,为什么它们不是零呢?因为它们被标准化了。所以我们减去了平均值,除以标准差。
xmb
'''
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
... ⋱ ...
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
[torch.FloatTensor of size 64x784 (GPU 0)]
'''
现在我们要做的是将其传递给我们的逻辑回归。所以我们可能会这样做,我们将使用vxmb(变量 x 小批量),我可以取出我的 x 小批量,我可以将其移动到 GPU 上,因为记住我的net2对象在 GPU 上,所以我们的数据也必须在 GPU 上。然后我要做的第二件事是,我必须将其包装在Variable中。那么变量是做什么的呢?这是我们免费获得自动微分的方式。PyTorch 可以自动微分几乎任何张量。但这需要内存和时间,所以它不会总是跟踪。要进行自动微分,它必须跟踪确切的计算方式。我们将这些东西相加,我们将其乘以那个,然后我们取了这个的符号等等。你必须知道所有的步骤,因为然后要进行自动微分,它必须使用链式法则对每个步骤求导,然后将它们相乘。所以这是缓慢和占用内存的。所以我们必须选择说“好的,这个特定的东西,我们以后会对其进行求导,所以请为我们跟踪所有这些操作。”我们选择的方式是将一个张量包装在Variable中。这就是我们的做法。
你会发现它看起来几乎和一个张量一样,但现在它说“包含这个张量的变量”。所以在 PyTorch 中,一个变量的 API 与张量完全相同,或者更具体地说,是张量 API 的超集。我们对张量可以做的任何事情,我们也可以对变量做。但它会跟踪我们做了什么,以便我们以后可以求导。
vxmb = Variable(xmb.cuda())
vxmb
'''
Variable containing:
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
... ⋱ ...
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
-0.4245 -0.4245 -0.4245 ... -0.4245 -0.4245 -0.4245
[torch.cuda.FloatTensor of size 64x784 (GPU 0)]
'''
所以我们现在可以将其传递给我们的net2对象。记住我说过你可以将其视为函数。所以请注意,我们没有调用.forward(),我们只是将其视为函数。然后记住,我们取了对数,为了撤销这个操作,我正在使用.exp(),这将给我概率。所以这是我的概率,它返回的大小是 64 乘以 10,所以对于小批量中的每个图像,我们有 10 个概率。你会看到,大多数概率都非常接近零。而其中一些则要大得多,这正是我们所希望的。就像好吧,它不是零,不是 1,不是 2,它是3,不是 4 等等。
preds = net2(vxmb).exp(); preds[:3]
'''
Variable containing:
Columns 0 to 5
1.6740e-03 1.0416e-05 2.5454e-05 1.9119e-02 6.5026e-05 9.7470e-01
3.4048e-02 1.8530e-04 6.6637e-01 3.5073e-02 1.5283e-01 6.4995e-05
3.0505e-08 4.3947e-08 1.0115e-05 2.0978e-04 9.9374e-01 6.3731e-05
Columns 6 to 9
2.1126e-06 1.7638e-04 3.9351e-03 2.9154e-04
1.1891e-03 3.2172e-02 1.4597e-02 6.3474e-02
8.9568e-06 9.7507e-06 7.8676e-04 5.1684e-03
[torch.cuda.FloatTensor of size 3x10 (GPU 0)]
'''
我们可以调用net2.forward(vxmb),它会做完全相同的事情。但这并不是 PyTorch 的所有机制实际上是如何工作的。他们实际上将其称为函数。这实际上是一个非常重要的想法,因为这意味着当我们定义自己的架构或其他内容时,任何你想要放入函数的地方,你都可以放入一个层;任何你想要放入一个层的地方,你都可以放入一个神经网络;任何你想要放入一个神经网络的地方,你都可以放入一个函数。因为就 PyTorch 而言,它们都只是它将调用的东西,就像它们是函数一样。所以它们是可以互换的,这是非常重要的,因为这就是我们通过混合和匹配许多部分并将它们组合在一起来创建非常好的神经网络的方式。
让我举个例子。这是我的逻辑回归,准确率达到了 91%多一点。我现在要把它转换成一个带有一个隐藏层的神经网络。

我要做的是创建更多的层。我要改变这个,使其输出 100 而不是 10,这意味着这个输入将是 100 而不是 10。现在这样还不能让事情变得更好。为什么这肯定不会比之前更好呢?因为两个线性层的组合只是一个线性层,但参数不同。

所以我们有两个线性层,这只是一个线性层。为了使事情变得有趣,我将用零替换第一层中的所有负数。因为这是一个非线性转换,这个非线性转换被称为修正线性单元(ReLU)。

所以nn.Sequential简单地会依次调用每个层对每个小批量进行操作。所以做一个线性层,用零替换所有负数,再做一个线性层,最后做一个 softmax。这现在是一个有一个隐藏层的神经网络。所以让我们尝试训练这个。准确率现在已经提高到 96%。

所以这个想法是,我们在这节课中学习的基本技术在你开始将它们堆叠在一起时变得强大。
问题:为什么你选择了 100?没有原因。输入一个额外的零更容易。神经网络层中应该有多少激活是深度学习从业者的规模问题,我们在深度学习课程中讨论过,而不是在这门课程中。
问题:在添加额外的层时,如果你做了两个 softmax,这会有影响吗,或者这是你不能做的事情?你绝对可以在那里使用 softmax。但这可能不会给你想要的结果。原因是 softmax 倾向于将大部分激活推向零。激活,只是为了明确,因为在深度学习课程中我收到了很多关于什么是激活的问题,激活是在一个层中计算出来的值。这就是一个激活:

这不是一个权重。权重不是一个激活。它是你从一个层计算出来的值。所以 softmax 会倾向于使大部分激活接近于零,这与你想要的相反。通常你希望你的激活尽可能丰富、多样且被使用。所以没有什么能阻止你这样做,但它可能不会工作得很好。基本上,你的所有层几乎都会跟随非线性激活函数,通常是 ReLU,除了最后一层。
问题:在做多层时,比如说 2 或 3 层,你想要改变这些激活层吗?不。所以如果我想要更深,我会直接这样做。

现在这是一个两个隐藏层的网络。
问题:所以我想我听到你说有几种不同的激活函数,比如修正线性单元。有一些例子,为什么会使用每一个呢?是的,很好的问题。所以基本上当你添加更多的线性层时,你的输入进来,你把它通过一个线性层然后一个非线性层,线性层,非线性层,线性层和最终的非线性层。最终的非线性层正如我们讨论过的,如果它是多类别分类但你只选择其中一个,你会使用 softmax。如果是二元分类或多标签分类,你会使用 sigmoid。如果是回归,通常你根本不会有,尽管我们在昨晚的深度学习课程中学到有时你也可以在那里使用 sigmoid。所以它们基本上是最终层的主要选项。对于隐藏层,你几乎总是使用 ReLU,但还有另一个你可以选择的,有点有趣,叫做 leaky ReLU。基本上如果它大于零,它是y = x,如果小于零,它就像y = 0.1x。所以它与 ReLU 非常相似,但不是等于 0,而是接近于 0。所以它们是主要的两种:ReLU 和 Leaky ReLU。

还有其他一些,但它们有点像那样。例如,有一种叫做 ELU 的东西相当受欢迎,但细节并不太重要。像 ELU 这样的东西有点像 ReLU,但在中间稍微弯曲一些。它通常不是基于数据集选择的东西。随着时间的推移,我们发现了更好的激活函数。所以两三年前,每个人都使用 ReLU。一年前,几乎每个人都使用 Leaky ReLU。今天,我想大多数人开始转向 ELU。但老实说,激活函数的选择实际上并不太重要。人们实际上已经表明,你可以使用相当任意的非线性激活函数,甚至是正弦波,它仍然有效。
所以尽管今天我们要做的是展示如何创建这个没有隐藏层的网络,将其转变为下面这个网络(下面)准确率为 96%左右将会很简单。这是你可能应该在这一周尝试做的事情,创建这个版本。

现在我们有了一个可以传递我们的变量并得到一些预测的网络,这基本上就是我们调用fit时发生的事情。所以我们将看看这种方法如何用于创建这种随机梯度下降。需要注意的一件事是将预测的概率转换为预测的数字是,我们需要使用 argmax。不幸的是,PyTorch 并不称之为 argmax。相反,PyTorch 只是称之为 max,并且 max 返回两个东西:它返回给定轴上的实际最大值(所以max(1)将返回列的最大值),它返回的第二件事是该最大值的索引。所以 argmax 的等价物是调用 max 然后获取第一个索引的东西:

这就是我们的预测。如果这是 numpy,我们将使用np.argmax()。
preds = predict(net2, md.val_dl).argmax(1)
plots(x_imgs[:8], titles=preds[:8])

所以这是我们手动创建的逻辑回归的预测,在这种情况下,看起来我们几乎全部正确。
接下来我们要尝试摆脱使用库的是我们将尝试避免使用矩阵乘法运算符。相反,我们将尝试手动编写。
广播[46:58]
因此,接下来,我们将学习一些似乎是一个小的编程概念的东西。但实际上,至少在我看来,这将是我们在这门课程中教授的最重要的编程概念,也可能是你需要构建机器学习算法的所有重要编程概念。这就是广播的概念。我将通过示例展示这个概念。
如果我们创建一个数组 10、6、-4 和一个数组 2、8、7,然后将它们相加,它会依次添加这两个数组的每个分量——我们称之为“逐元素”。
a = np.array([10, 6, -4])
b = np.array([2, 8, 7]) a + b
'''
array([12, 14, 3])
'''
换句话说,我们不必编写循环。在过去,我们必须循环遍历每一个并将它们相加,然后将它们连接在一起。今天我们不必这样做。它会自动为我们发生。因此,在 numpy 中,我们自动获得逐元素操作。我们可以用 PyTorch 做同样的事情。在 Fast AI 中,我们只需添加一个大写 T 来将某物转换为 PyTorch 张量。如果我们将它们相加,结果完全相同。

因此,这些库中的逐元素操作在这种情况下是相当标准的。有趣的不仅仅是因为我们不必编写 for 循环,而且实际上更有趣的是由于这里发生的性能问题。
性能
第一个是如果我们在 Python 中进行 for 循环,那将会发生。即使你使用 PyTorch,它仍然在 Python 中执行 for 循环。它没有优化 for 循环的方法。因此,在 Python 中,for 循环的速度大约比在 C 中慢 10,000 倍。这是你的第一个问题。我记不清是 1,000 还是 10,000。
然后,第二个问题是,你不仅希望它在 C 中得到优化,而且你希望 C 利用你所有 CPU 所做的事情,这被称为 SIMD,单指令多数据。你的 CPU 能够一次处理 8 个向量中的 8 个元素,并将它们相加到另一个包含 8 个元素的向量中,在一个 CPU 指令中。因此,如果你能利用 SIMD,你立即就会快 8 倍。这取决于数据类型有多大,可能是 4,可能是 8。
你的计算机中还有多个进程(多个核心)。因此,如果向量相加发生在一个核心中,你可能有大约 4 个核心。因此,如果你使用 SIMD,你会快 8 倍,如果你可以使用多个核心,那么你会快 32 倍。然后如果你在 C 中这样做,你可能会快 32k 倍。
所以好处是当我们执行a + b时,它利用了所有这些东西。
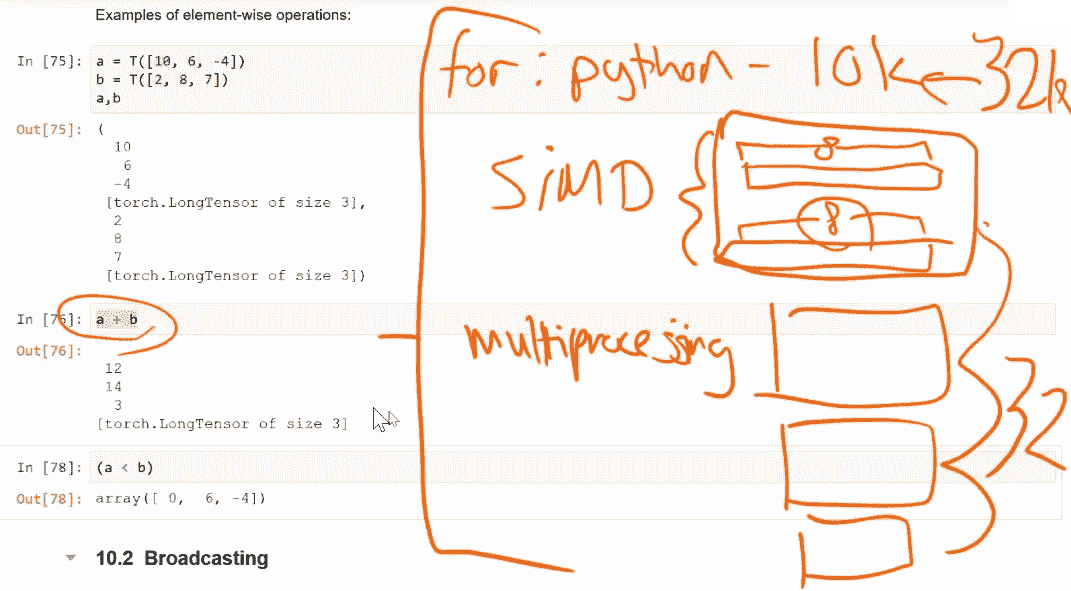
更好的是,如果你在 PyTorch 中执行这个操作,并且你的数据是用.cuda()创建的,然后将其放在 GPU 上,那么你的 GPU 可以一次执行大约 10,000 个操作。因此,这将比 C 快 100 倍。因此,这对于获得良好的性能至关重要。你必须学会如何通过利用这些逐元素操作来编写无循环的代码。这不仅仅是加号(+)。我还可以使用小于号(<),这将返回 0,1,1。

或者如果我们回到 numpy,False,True,True。

因此,你可以使用这个来做各种事情而不需要循环。例如,我现在可以将其乘以a,这里是所有小于b的a的值:

或者我们可以取平均值:
(a < b).mean()
'''
0.66666666666666663
'''
这是a中小于b的值的百分比。因此,你可以用这个简单的想法做很多事情。
进一步
但要进一步,要进一步超越这种逐元素操作,我们将不得不走到下一步,到一种称为广播的东西。让我们从看一个广播的例子开始。
a
'''
array([10, 6, -4])
'''
a 是一个具有一维的数组,也称为秩 1 张量,也称为向量。我们可以说a大于零:
a > 0
'''
array([ True, True, False], dtype=bool)
'''
这里,我们有一个秩 1 张量(a)和一个秩 0 张量(0)。秩 0 张量也称为标量,秩 1 张量也称为向量。我们之间有一个操作:

现在你可能已经做了一千次,甚至没有注意到这有点奇怪。你有不同等级和不同大小的这些东西。那么它实际上在做什么呢?它实际上是将那个标量复制 3 次(即[0, 0, 0]),并实际上逐个元素地给我们三个答案。这就是所谓的广播。广播意味着复制我的张量的一个或多个轴,以使其与另一个张量的形状相同。但它实际上并没有复制。它实际上是存储了一种内部指示器,告诉它假装这是一个三个零的向量,但实际上它不是去下一行或下一个标量,而是回到它来的地方。如果你对这个特别感兴趣,它们将该轴上的步幅设置为零。这对于那些好奇的人来说是一个较为高级的概念。
所以我们可以做 a + 1[54:52]。它将广播标量 1 为[1, 1, 1],然后进行逐元素加法。
a + 1
'''
array([11, 7, -3])
'''
我们可以对一个矩阵做同样的操作。这是我们的矩阵。
m = np.array([[1, 2, 3], [4,5,6], [7,8,9]]); m
'''
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
'''
那个矩阵的 2 倍将广播 2 为[[2, 2, 2],[2,2,2],[2,2,2]],然后进行逐元素乘法。这就是我们广播的最简单版本。
2*m
'''
array([[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18]])
'''
将向量广播到矩阵[55:27]
这是广播的一个稍微复杂的版本。这里有一个名为c的数组。这是一个秩 1 张量。
c = np.array([10,20,30]); c
'''
array([10, 20, 30])
'''
这是之前的矩阵m——秩 2 张量。我们可以添加m + c。那么这里发生了什么?
m + c
'''
array([[11, 22, 33],
[14, 25, 36],
[17, 28, 39]])
'''
你可以看到它所做的是将[10, 20, 30]添加到每一行。

所以我们可以想象它似乎做了与广播标量相同类型的想法,就像复制了它。然后将这些视为秩 2 矩阵。现在我们可以进行逐元素加法。
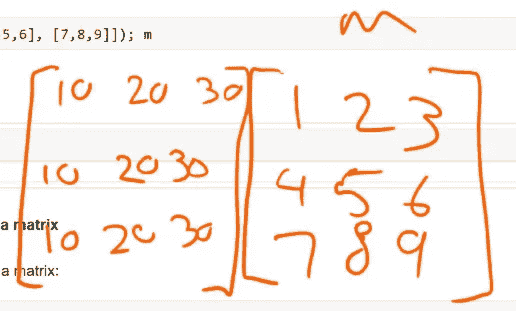
问题:通过查看这个例子,它将其复制下来生成新的行。如果我们想要获得新的列,我们应该如何做[56:50]?我很高兴你问了。所以我们会这样做:

现在将其视为我们的矩阵。要让 numpy 这样做,我们需要传入一个矩阵而不是一个向量,而是传入一个具有一列的矩阵(即秩 2 张量)。基本上,numpy 会将这个秩 1 张量视为秩 2 张量,表示一行。换句话说,它是 1 乘 3。所以我们想要创建一个 3 乘 1 的张量。有几种方法可以做到这一点。一种方法是使用np.expand_dims(c,1),如果你传入这个参数,它会说“请在这里插入一个长度为 1 的轴”。所以在我们的情况下,我们想将其转换为 3 乘 1,所以如果我们说expand_dims(c,1),它会将形状改变为(3, 1)。所以如果我们看看它是什么样子的,它看起来像一列。
np.expand_dims(c,1).shape
'''
(3, 1)
'''
np.expand_dims(c,1)
'''
array([[10],
[20],
[30]])
'''
所以如果我们现在加上m,你可以看到它确实做了我们希望它做的事情,即将 10、20、30 添加到列[58:50]:
m + np.expand_dims(c,1)
'''
array([[11, 12, 13],
[24, 25, 26],
[37, 38, 39]])
'''
现在由于单位轴的位置是如此重要,所以通过实验创建这些额外的单位轴并知道如何轻松地做到这一点是非常有帮助的。在我看来,np.expand_dims并不是最容易的方法。最简单的方法是使用一个特殊的索引None来索引张量。None的作用是在那个位置创建一个长度为 1 的新轴。因此,这将在开始添加一个新的长度为 1 的轴。
c[None]
'''
array([[10, 20, 30]])
'''
c[None].shape
'''
(1, 3)
'''
这将在末尾添加一个新的长度为 1 的轴。
c[:,None]
'''
array([[10],
[20],
[30]])
'''
c[:,None].shape
'''
(3, 1)
'''
或者为什么不两者都做呢
c[None,:,None].shape
'''
(1, 3, 1)
'''
所以如果你考虑一下,一个张量中有 3 个元素,可以是任何你喜欢的阶数,你可以随意添加单位轴。这样,我们可以决定我们希望广播的方式。所以在 numpy 中有一个非常方便的东西叫做broadcast_to,它的作用是将我们的向量广播到那个形状,并展示给我们看看那会是什么样子。
np.broadcast_to(c, (3,3))
'''
array([[10, 20, 30],
[10, 20, 30],
[10, 20, 30]])
'''
所以如果你对某个广播操作中发生的事情感到不确定,你可以使用broadcast_to。例如,在这里,我们可以说,而不是(3,3),我们可以说m.shape,看看将会发生什么。
np.broadcast_to(c, m.shape)
'''
array([[10, 20, 30],
[10, 20, 30],
[10, 20, 30]])
'''
这就是在我们将其添加到m之前会发生的事情。所以如果我们说将其转换为列,那就是它的样子:
np.broadcast_to(c[:,None], m.shape)
'''
array([[10, 10, 10],
[20, 20, 20],
[30, 30, 30]])
'''
所以这就是广播的直观定义。现在希望我们可以回到那个 numpy 文档并理解它的含义。
从Numpy 文档 [1:01:37]:
广播这个术语描述了 numpy 在算术运算期间如何处理具有不同形状的数组。在一定的约束条件下,较小的数组(较低秩的张量)被“广播”到较大的数组上,以便它们具有兼容的形状。广播提供了一种向量化数组操作的方法,使循环发生在 C 而不是 Python 中。它可以在不进行不必要的数据复制的情况下实现这一点,并通常导致高效的算法实现。
“向量化”通常意味着使用 SIMD 等技术,以便多个操作同时进行。它实际上并不会进行不必要的数据复制,只是表现得好像进行了复制。所以这就是我们的定义。
现在在深度学习中,你经常处理 4 阶或更高阶的张量,并且经常将它们与 1 阶或 2 阶的张量结合在一起,仅凭直觉正确地执行这些操作几乎是不可能的。所以你真的需要了解规则。

这里是m.shape和c.shape [1:02:45]。所以规则是我们将逐个元素地比较我们两个张量的形状。我们将一次查看一个,并且我们将从末尾开始向前移动。当这两个条件之一为真时,两个维度将是兼容的。所以让我们检查一下我们的m和c是否兼容。所以我们将从末尾开始(首先是尾部维度)并检查“它们是否兼容?”如果维度相等,则它们是兼容的。让我们继续下一个。哦,我们缺少了。c缺少一些东西。如果有东西缺失会发生什么,我们会插入一个 1。这就是规则。所以现在让我们检查一下——这些是否兼容?其中一个是 1,是的,它们是兼容的。所以现在你可以看到为什么 numpy 将一维数组视为一个代表行的 2 阶张量。这是因为我们基本上在前面插入了一个 1。这就是规则。

在对两个数组进行操作时,Numpy/PyTorch 会逐个元素地比较它们的形状。它从尾部维度开始,逐步向前推进。当两个维度兼容时
-
它们是相等的,或者
-
其中之一是 1
数组不需要具有相同数量的维度。例如,如果你有一个256*256*3的 RGB 值数组,并且你想要按不同的值缩放图像中的每种颜色,你可以将图像乘以一个具有 3 个值的一维数组。根据广播规则对齐这些数组的尾部轴的大小,显示它们是兼容的:
Image (3d array): 256 x 256 x 3
Scale (1d array): 3
Result (3d array): 256 x 256 x 3
例如,上面是你经常需要做的事情,即你从一幅图像开始,256 像素乘以 256 像素乘以 3 个通道。你想要减去每个通道的平均值。所以你有 256 乘以 256 乘以 3,你想要减去长度为 3 的东西。是的,你可以做到。绝对可以。因为 3 和 3 是兼容的,因为它们是相同的。256 和空是兼容的,因为它会插入一个 1。256 和空是兼容的,因为它会插入一个 1。所以你最终会得到这个(每个通道的平均值)会在所有这个轴(从右边数第二个)上广播,然后整个东西将在这个最左边的轴上广播,所以我们最终会得到一个 256 乘以 256 乘以 3 的有效张量。
有趣的是,数据科学或机器学习社区中很少有人理解广播,大多数时候,例如,当我看到人们为计算机视觉进行预处理时,比如减去平均值,他们总是在通道上写循环。我认为不必这样做非常方便,而且通常不必这样做速度更快。所以如果你擅长广播,你将拥有这种非常少数人拥有的超级有用的技能。这是一种古老的技能。它可以追溯到 APL 的时代。APL 是上世纪 50 年代的,代表着 A Programming Language,肯尼斯·艾弗森写了一篇名为“符号作为思维工具”的论文,他在其中提出了一种新的数学符号。他提出,如果我们使用这种新的数学符号,它会给我们提供新的思维工具,让我们能够思考以前无法思考的事情。他的一个想法就是广播,不是作为计算机编程工具,而是作为数学符号的一部分。因此,他最终将这种符号实现为一种思维工具,作为一种名为 APL 的编程语言。他的儿子继续将其进一步发展为一种名为 J 的软件,这基本上是当你将 60 年来非常聪明的人们致力于这个想法时得到的结果。通过这种编程语言,你可以用一两行代码表达非常复杂的数学思想。我们有 J 是很棒的,但更棒的是这些想法已经进入我们所有人使用的语言中,比如在 Python 中的 numpy 和 PyTorch 库。这些不仅仅是一些小众的想法,它们是思考数学和进行编程的基本方式。
让我举个例子,这种符号作为思维工具的例子。这里我们有 c:

这里我们有 c[None]:

注意现在有两个方括号。这有点像一个一行向量张量。这里是一个小列:

这将会做什么呢?

所以从广播规则的角度来看,我们基本上是将这个列(维度为(3,1))和这个行(维度为(1,3))进行操作。为了使这些符合我们的广播规则,列必须被复制 3 次,因为它需要匹配 3。行必须被复制 3 次以匹配 3。所以现在我有两个矩阵可以进行逐元素乘积。

所以正如你所说,这是我们的外积。

现在有趣的是,突然间这不再是一个特殊的数学案例,而只是广播这个一般概念的一个特定版本,我们可以像外加一样:

或者外大于:

或者其他。所以突然间我们有了这个概念,我们可以用它来构建新的想法,然后我们可以开始尝试这些新的想法。
有趣的是,numpy 有时会使用这个方法。例如,如果你想创建一个网格,numpy 就是这样做的:

实际上返回的是 0、1、2、3、4;一个作为列,一个作为行。所以我们可以说好的,这是 x 网格(xg)逗号 y 网格(yg),现在你可以做类似这样的事情:

所以突然间我们把它扩展成了一个网格。所以有趣的是一些简单的概念是如何被不断地建立和发展的。所以如果你熟悉 APL 或 J,这是一个由许多层层叠加而成的整个环境。虽然在 numpy 中我们没有这样深层次的环境,但你肯定可以看到这种广播的想法在简单的事情中体现出来,比如我们如何在 numpy 中创建一个网格。
实现矩阵乘法[1:12:30]
这就是广播,现在我们可以使用这个来实现矩阵乘法。那么为什么我们要这样做呢?显然我们不需要。矩阵乘法已经被我们的库完美地处理了。但是很多时候你会发现在各种领域,特别是在深度学习中,会有一些特定类型的线性函数,你想要做的事情并没有完全为你做好。例如,有一个叫做张量回归和张量分解的领域,目前正在得到很大的发展,它们讨论的是如何将高阶张量转化为行、列和面的组合。事实证明,当你这样做时,你基本上可以处理非常高维的数据结构,而不需要太多的内存和计算时间。例如,有一个非常棒的库叫做TensorLy,它为你做了很多这样的事情。所以这是一个非常重要的领域。它涵盖了所有的深度学习,还有很多现代机器学习。所以即使你不会定义矩阵乘法,你很可能会想要找到一些其他略有不同的张量积。所以了解如何做这个是非常有用的。
让我们回过头来看看我们的二维数组和一维数组,秩为 2 的张量和秩为 1 的张量[1:14:27]。
m, c
'''
(array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]), array([10, 20, 30]))
'''
记住,我们可以使用@符号或旧方法np.matmul进行矩阵乘法。当我们这样做时,实际上我们基本上是在说1*10 + 2*20 + 3*30 = 140,所以我们对每一行都这样做,然后我们可以继续对下一行做同样的事情,依此类推以获得我们的结果。
m @ c # np.matmul(m, c)
'''
array([140, 320, 500])
'''
你也可以在 PyTorch 中这样做
T(m) @ T(c)
'''
140
320
500
[torch.LongTensor of size 3]
'''
但是(m * c)这不是矩阵乘法。那是什么?逐元素广播。但请注意,它创建的数字[10, 40, 90]正是我在做矩阵乘法的第一部分时需要计算的三个确切数字(1*10 + 2*20 + 3*30)。
m * c
'''
array([[ 10, 40, 90],
[ 40, 100, 180],
[ 70, 160, 270]])
'''
换句话说,如果我们对列求和,即轴等于 1,我们就得到了矩阵向量乘积:
(m * c).sum(axis=1)
'''
array([140, 320, 500])
'''
所以我们可以在不依赖库的特殊帮助下做这些事情。现在让我们将这扩展到矩阵矩阵乘积。

matrixmultiplication.xyz/
矩阵矩阵乘积看起来是这样的。有一个很棒的网站叫做matrixmultiplication.xyz,它向我们展示了当我们将两个矩阵相乘时会发生什么。从操作的角度来看,这就是矩阵乘法。换句话说,我们刚刚做的是首先取第一列和第一行相乘得到 15:

然后我们取第二列和第一行得到 27:

所以我们基本上是在做我们刚刚做的事情,矩阵向量乘积,我们只是做了两次。一次用这一列(左边),一次用那一列(右边),然后我们把这两个连接在一起。所以我们现在可以继续这样做:
(m * n[:,0]).sum(axis=1)
'''
array([140, 320, 500])
'''
(m * n[:,1]).sum(axis=1)
'''
array([ 25, 130, 235])
'''
这就是我们矩阵乘法的两列。
我不想让我们的代码太乱,所以我不打算真的使用那个,但是现在我们有了它,如果我们想要的话。我们不再需要使用 torch 或 numpy 矩阵乘法。我们有自己的方法可以使用,只使用逐元素操作、广播和求和。
这是我们从头开始的逻辑回归类[1:18:37]。我只是把它复制到这里。
class LogReg(nn.Module):
def __init__(self):
super().__init__()
self.l1_w = get_weights(28*28, 10) # Layer 1 weights
self.l1_b = get_weights(10) # Layer 1 bias
def forward(self, x):
x = x.view(x.size(0), -1)
x = x @ self.l1_w + self.l1_b
return torch.log(softmax(x))
这是我们实例化对象的地方,复制到 GPU。我们创建一个优化器,我们将在稍后学习。然后我们调用 fit。
net2 = LogReg().cuda()
opt=optim.Adam(net2.parameters())
fit(net2, md, n_epochs=1, crit=loss, opt=opt, metrics=metrics)
'''
[ 0\. 0.31102 0.28004 0.92406]
'''
编写我们自己的训练循环[1:18:53]
所以目标是现在重复这一过程,而无需调用 fit。为此,我们需要一个循环,每次抓取一个小批量的数据。对于每个小批量的数据,我们需要将其传递给优化器,并说“请尝试为这个小批量提供稍微更好的预测”。
正如我们学到的,为了一次抓取训练集的一个小批次,我们必须向模型数据对象请求训练数据加载器。我们必须将其包装在iter中以创建一个迭代器或生成器。这样就给我们了我们的数据加载器。所以 PyTorch 将其称为数据加载器。我们实际上编写了自己的 Fast AI 数据加载器,但基本上是相同的思路。
dl = iter(md.trn_dl) # Data loader
接下来我们要做的是获取 x 和 y 张量,从我们的数据加载器中获取下一个。将其包装在Variable中以表明我需要能够对使用此计算的导数进行求导。因为如果我不能求导,那么我就无法得到梯度,也无法更新权重。而且我需要将其放在 GPU 上,因为我的模块在 GPU 上(net2 = LogReg().cuda())。所以现在我们可以将该变量传递给我们实例化的对象(即我们的逻辑回归)。记住,我们的模块,我们可以将其用作函数,因为这就是 PyTorch 的工作原理。这给我们提供了一组预测,就像我们以前看到的那样。
xt, yt = next(dl)
y_pred = net2(Variable(xt).cuda())
现在我们可以检查损失[1:20:41]。我们定义损失为负对数似然损失对象。我们将在下一课中学习如何计算它,现在,只需将其视为分类问题的均方根误差。所以我们也可以像调用函数一样调用它。所以你可以看到这在 PyTorch 中是一个非常普遍的想法,将一切都理想地视为函数。在这种情况下,我们有一个负对数似然损失对象,我们可以将其视为函数。我们传入我们的预测和实际值。同样,实际值需要转换为变量并放在 GPU 上,因为损失是我们实际想要求导的东西。这给我们带来了我们的损失,就是这样。
l = loss(y_pred, Variable(yt).cuda())
print(l)
'''
Variable containing:
2.4352
[torch.cuda.FloatTensor of size 1 (GPU 0)]
'''
这是我们的损失 2.43。所以它是一个变量,因为它是一个变量,它知道它是如何计算的。它知道它是用这个损失函数(loss)计算的。它知道预测是用这个网络(net2)计算的。它知道这个网络由这些操作组成:

所以我们可以自动获取梯度。要获取梯度,我们调用l.backward()。记住l是包含我们损失的东西。所以l.backward()是添加到任何变量的东西。然后调用.backward(),这表示请计算梯度。这样就计算了梯度并将其存储在内部,基本上对于用于计算的每个权重/参数,现在都存储在.grad中,我们稍后会看到,但基本上存储了梯度。然后我们可以调用optimizer.step(),我们很快将手动执行这一步。这部分表示请让权重变得更好一点。

optimizer.step [1:22:49]
因此,optimizer.step()正在做的是,如果你有一个非常简单的函数像这样,优化器所做的就是说好的,让我们选择一个起始点,计算损失的值,计算导数告诉我们哪个方向是向下的。因此,它告诉我们我们需要朝那个方向走。然后我们迈出一小步。

然后我们再次取导数,采取一个小步骤,并重复,直到最终我们采取的步骤如此之小以至于停止。

这就是梯度下降的作用。小步骤有多大?基本上在这里取导数,所以让我们说导数是 8。然后我们乘以一个小数,比如 0.01,这告诉我们要采取什么步骤大小。这里的这个小数被称为学习率,它是设置的最重要的超参数。如果你选择的学习率太小,那么你的下降步骤将会很小,而且会花费很长时间。学习率太大,你会跳得太远,然后你会跳得太远,最终会发散而不是收敛。

在这节课中我们不会讨论如何选择学习率,但在深度学习课程中,我们实际上向你展示了一种非常可靠地选择一个非常好的学习率的特定技术。
因此,基本上正在发生的是,我们计算导数,我们调用执行step的优化器,换句话说,根据梯度和学习率更新权重。
希望在这样做之后,我们的损失比之前更好。因此,我刚刚重新运行了这个,得到了一个 4.16 的损失。

一步之后,现在是 4.03。

所以它按照我们希望的方式运行,基于这个小批量,它更新了我们网络中的所有权重,使它们比之前更好。因此,我们的损失下降了。
训练循环
因此,让我们将其转化为一个训练循环。我们将进行一百步:
-
从数据加载器中获取另一个小批量数据
-
从我们的网络中计算预测
-
从预测和实际值计算我们的损失
-
每 10 次,我们将打印出准确率,只需取平均值,看它们是否相等。
-
一个 PyTorch 特定的事情,你必须将梯度清零。基本上,你可以有许多不同的损失函数的网络,你可能想要将所有的梯度加在一起。因此,你必须告诉 PyTorch 何时将梯度设置为零。因此,这只是说将所有的梯度设置为零。
-
计算梯度,这被称为反向传播
-
然后进行一步优化器,使用梯度和学习率更新权重
for t in range(100):
xt, yt = next(dl)
y_pred = net2(Variable(xt).cuda())
l = loss(y_pred, Variable(yt).cuda())
if t % 10 == 0:
accuracy = np.mean(to_np(y_pred).argmax(axis=1) == to_np(yt))
print("loss: ", l.data[0], "\t accuracy: ", accuracy)
optimizer.zero_grad()
l.backward()
optimizer.step()
'''
loss: 2.2104923725128174 accuracy: 0.234375
loss: 1.3094730377197266 accuracy: 0.625
loss: 1.0296542644500732 accuracy: 0.78125
loss: 0.8841525316238403 accuracy: 0.71875
loss: 0.6643403768539429 accuracy: 0.8125
loss: 0.5525785088539124 accuracy: 0.875
loss: 0.43296846747398376 accuracy: 0.890625
loss: 0.4388267695903778 accuracy: 0.90625
loss: 0.39874207973480225 accuracy: 0.890625
loss: 0.4848807752132416 accuracy: 0.875
'''
一旦我们运行它,你会看到损失下降,准确率上升。所以这是基本的方法。下一课,我们将看到optimizer.step()做了什么。我们将详细看一下。我们不会深入研究l.backward(),因为我说过我们基本上会将导数的计算视为给定的。但基本上,在任何深度网络中,你有一个类似于线性函数的函数,然后将其输出传递到另一个可能类似于 ReLU 的函数中。然后将其输出传递到可能是另一个线性层的函数中,依此类推:
i( h( g( f(x) ) ) )
因此,这些深度网络只是函数的函数的函数。因此,你可以用数学方式写出它们。因此,反向传播所做的就是说(让我们将其简化为深度为二的版本),我们可以说:
g( f(x) )
u = f(x)
因此,我们可以用链式法则计算*g(f(x))*的导数:
g'(u) f'(x)
所以你可以看到,我们可以对函数的函数的函数做同样的事情。因此,当你将一个函数应用于一个函数的函数时,你可以通过将这些层的导数的乘积来计算导数。在神经网络中,我们称之为反向传播。因此,当你听到反向传播时,它只是意味着使用链式法则来计算导数。
所以当你看到一个神经网络像这样定义时:

如果按顺序定义,字面上,所有这意味着将这个函数应用于输入,将这个函数应用于那个,将这个函数应用于那个,依此类推。因此,这只是定义了一个函数到一个函数到一个函数到一个函数的组合。因此,虽然我们不打算自己计算梯度,但现在你可以看到为什么它可以这样做,只要它内部知道幂函数的导数是什么,正弦函数的导数是什么,加法的导数是什么,依此类推。然后我们在这里的 Python 代码只是将这些东西组合在一起。因此,它只需要知道如何用链式法则将它们组合在一起,然后就可以运行了。
所以我认为我们现在可以把它留在这里,在下一堂课中,我们将看看如何编写我们自己的优化器,然后我们将自己从头解决 MNIST 问题。到时见!
机器学习 1:第 10 课
原文:
medium.com/@hiromi_suenaga/machine-learning-1-lesson-10-6ff502b2db45译者:飞龙
协议:CC BY-NC-SA 4.0
来自机器学习课程的个人笔记。随着我继续复习课程以“真正”理解它,这些笔记将继续更新和改进。非常感谢 Jeremy 和 Rachel 给了我这个学习的机会。
pip 上的 Fast AI [0:00]
欢迎回到机器学习!这周最令人兴奋的事情当然是 Fast AI 现在在 pip 上了,所以你可以pip install fastai:
fastai 使得使用 PyTorch 进行深度学习更快、更准确、更容易
pypi.org](https://pypi.org/project/fastai/?source=post_page-----6ff502b2db45--------------------------------)
最简单的方法可能仍然是执行conda env update,但有几个地方更方便的是执行pip install fastai,如果你在笔记本之外的地方工作,那么这将使你在任何地方都可以访问 Fast AI。他们还向 Kaggle 提交了一个拉取请求,试图将其添加到 Kaggle 内核中。所以希望你很快就能在 Kaggle 内核上使用它。你可以在工作中或其他地方使用它,所以这很令人兴奋。我不会说它已经正式发布了。显然,现在还很早,我们仍在添加(你也在帮助添加)文档和所有这些东西。但很高兴现在有这个。
Kaggle 内核 [1:22]
这周有几个来自 USF 学生的很酷的内核。我想强调两个都来自文本规范化竞赛的内核,该竞赛旨在尝试将标准英语文本转换为文本,还有一个俄语的。你要尝试识别可能是“第一,第二,第三”之类的东西,并说这是一个基数,或者这是一个电话号码或其他什么。我快速搜索了一下,发现学术界曾尝试使用深度学习来做这个,但他们没有取得太多进展,实际上我注意到Alvira 的内核在这里得到了 0.992 的排名,我认为是前 20 名。这完全是启发式的,是特征工程的一个很好的例子。在这种情况下,整个事情基本上完全是特征工程。基本上是通过查看和使用大量正则表达式来弄清楚每个标记是什么。我认为她在这里做得很好,清楚地列出了所有不同的部分以及它们如何相互配合。她提到她也许希望将这个变成一个库,我认为这将是很好的。你可以使用它来提取文本中的所有部分。这是自然语言处理社区希望能够做到的事情,而不需要像这样大量手写代码。但目前,我很感兴趣看看获胜者到底做了什么,但我还没有看到机器学习被用来做这个特别好。也许最好的方法是将这种特征工程与一些机器学习结合起来。但我认为这是一个有效特征工程的很好例子。
这位是另一位 USF 的学生,她做了类似的事情,得到了类似的分数,但使用了自己不同的规则。同样,这也会让你在排行榜上获得一个不错的位置。所以我觉得看到我们的一些学生参加比赛并通过基本的手写启发式方法获得前 20 名结果的例子很有趣。这就是,例如,六年前的计算机视觉仍然是这样。基本上最好的方法是大量仔细手写的启发式方法,通常结合一些简单的机器学习。所以我认为随着时间的推移,这个领域肯定在努力向更多自动化方向发展。
波尔图塞古罗的安全驾驶员预测获奖者 [4:21]
实际上有趣的是,在刚刚结束的安全驾驶员预测比赛中,一个 Netflix 奖获得者赢得了这个比赛,他发明了一种处理结构化数据的新算法,基本上不需要任何特征工程。所以他使用了五个深度学习模型和一个梯度提升机获得了第一名。他的基本方法与我们迄今为止在这门课程中学到的以及明天将要学习的内容非常相似,即使用全连接的神经网络和独热编码,特别是我们将要学习的嵌入。但他有一个非常聪明的技巧,就是在这个比赛中有很多未标记的数据。换句话说,他们不知道那个司机是否会提出索赔。所以当你有一些标记和一些未标记的数据时,我们称之为半监督学习。在现实生活中,大多数学习都是半监督学习。在现实生活中,通常有一些被标记的东西和一些未被标记的东西。所以这是最实用的学习方式。而结构化数据是公司日常处理的最常见的数据类型。所以这个比赛是一个半监督的、结构化数据比赛,使其非常实用。
所以他赢得比赛的技巧是进行数据增强,你们在深度学习课程中学到的,基本上就是这样的想法,比如如果你有图片,你会水平翻转它们或者稍微旋转一下。数据增强意味着创建新的数据示例,这些示例是你已经拥有的数据的略微不同的版本。他的做法是对于数据中的每一行,他会随机地用另一行替换 15%的变量。所以现在每一行代表的是原始行的 85%混合,15%是随机选择的另一行。这是一种随机改变数据的方法,然后他使用了一种叫做自动编码器的东西,我们可能要等到深度学习课程的第二部分才会学习,但自动编码器的基本思想是你的因变量与自变量相同。换句话说,你试图预测你的输入,如果你被允许进行恒等变换,例如,显然可以轻松地预测输入,但自动编码器的技巧是至少在一个层中具有比输入更少的激活。所以如果你的输入是一个百维向量,你通过一个 100 乘以 10 的矩阵,创建十个激活,然后必须从中创建原始的 100 维向量。那么你基本上已经有效地对其进行了压缩。事实证明,这种类型的神经网络被迫在数据中找到相关性、特征和有趣的关系,即使数据没有标记。所以他使用了这个而不是进行任何手工工程。这些是一些有趣的方向,如果你继续进行机器学习研究,特别是如果你明年参加深度学习课程的第二部分,你会学到的。你可以看到特征工程正在消失,这就是刚刚一个小时前。所以这确实是非常近期的。但这是我长时间以来看到的最重要的突破之一。
MNIST 继续[8:32]
笔记本
这(LogReg)是我们创建的那个小手写的nn.Module类[9:15]。我们定义了损失。我们定义了学习率,我们定义了优化器。optim.SGD是我们接下来要尝试手写的东西。所以nn.NLLLoss和optim.SGD,我们是从 PyTorch 中借鉴的,但我们自己编写了模块LogReg和训练循环。
net2 = LogReg().cuda()
loss=nn.NLLLoss()
learning_rate = 1e-2
optimizer=optim.SGD(net2.parameters(), lr=learning_rate)
for epoch in range(1):
losses=[]
dl = iter(md.trn_dl)
for t in range(len(dl)):
# Forward pass: compute predicted y and loss by passing x to
# the model.
xt, yt = next(dl)
y_pred = net2(V(xt))
l = loss(y_pred, V(yt))
losses.append(l)
# Before the backward pass, use the optimizer object to zero
# all of the gradients for the variables it will update
# (which are the learnable weights of the model)
optimizer.zero_grad()
# Backward pass: compute gradient of the loss with respect
# to model parameters
l.backward()
# Calling the step function on an Optimizer makes an update
# to its parameters
optimizer.step()
val_dl = iter(md.val_dl)
val_scores = [score(*next(val_dl)) for i in range(len(val_dl))]
print(np.mean(val_scores))
所以基本思想是我们将经历一些时期[9:39],所以让我们经历一个时期。我们将跟踪每个小批次的损失,以便在最后报告。我们将把我们的训练数据加载器转换为迭代器,以便我们可以循环遍历它 - 遍历每个小批次。现在我们可以继续说for张量in数据加载器的长度,然后我们可以调用next来从该迭代器中获取下一个自变量和因变量。
然后记住,我们可以通过调用模型来将 x 张量(xt)传递给我们的模型,就好像它是一个函数一样。但首先,我们必须将其转换为一个变量。上周,我们在输入Variable(blah).cuda()来将其转换为一个变量,Fast AI 中的一个简写是大写V。所以张量的大写T,变量的大写V。这只是 Fast AI 中的一个快捷方式。这将返回我们的预测。
接下来我们需要做的是计算我们的损失,因为如果我们没有计算损失,就无法计算损失的导数。所以损失接受预测值和实际值。实际值再次是 y 张量,我们必须将其转换为一个变量。变量跟踪所有计算步骤。实际上,在 PyTorch 网站上有一个很棒的教程。
接下来我们需要做的是计算我们的损失,因为如果我们没有计算损失,就无法计算损失的导数。所以损失接受预测值和实际值。实际值再次是 y 张量,我们必须将其转换为一个变量。变量跟踪所有计算步骤。实际上,在 PyTorch 网站上有一个很棒的教程。在 PyTorch 网站上,有一个教程部分,其中有一个关于 Autograd 的教程。Autograd 是随 PyTorch 一起提供的自动微分包的名称,它是自动微分的实现。因此,Variable 类是真正的关键类,因为它可以将张量转换为我们可以跟踪其梯度的东西。基本上在这里他们展示了如何创建一个变量,对变量进行操作,然后可以回头查看 grad 函数(grad_fn),这是它跟踪以计算梯度的函数。因此,当我们对这个变量和从该变量计算出的变量进行更多操作时,它会继续跟踪。稍后,我们可以进行.backward(),然后打印.grad并找出梯度。所以你会注意到我们从未定义过梯度,我们只是定义它为(x + 2)² * 3之类的表达式,它可以计算梯度。
这就是为什么我们需要将其转换为一个变量。所以l现在是一个包含损失的变量。它包含了这个小批量的损失的单个数字。但它不仅仅是一个数字。它是一个作为变量的数字,所以它是一个知道如何计算的数字。
我们将把这个损失添加到我们的数组中,这样我们以后可以得到它的平均值。现在我们要计算梯度。所以l.backward()是一个指令,表示计算梯度。所以记住当我们调用网络时,实际上是调用我们的前向函数。这就像是向前走一遍。然后向后就像是使用链式法则向后计算梯度。
optimizer.step()是我们即将编写的内容,即根据梯度和学习率更新权重。zero_grad(),我们将在手动编写时解释。

然后最后,我们可以将验证数据加载器转换为迭代器。然后我们可以遍历它的长度,每次取出一个 x 和 y,并询问我们定义的分数,即你预测了哪个,实际上是哪个,并检查它们是否相等。然后这些的平均值将是我们的准确率。
def score(x, y):
y_pred = to_np(net2(V(x)))
return np.sum(y_pred.argmax(axis=1) == to_np(y))/len(y_pred)
问题: 为什么你要将其转换为迭代器而不是使用普通的 Python 循环[14:53]?我们正在使用普通的 Python 循环,所以问题实际上是与什么进行比较。所以,也许你在考虑的替代方案可能是,我们可以使用类似带有索引器的列表。问题在于我们每次获取一个新的小批次时,我们希望它是随机的。我们希望有一个不同的洗牌过的东西。所以这个for t in range(len(dl)),你实际上可以无限迭代。你可以循环遍历它任意次数。所以这种想法在不同的语言中被称为不同的东西,但很多语言称之为流处理,这是一种基本的想法,而不是说我想要第三个或第九个东西,而是说我想要下一个东西。这对网络编程非常有用——从网络中获取下一个东西。对于 UI 编程也非常有用——获取下一个事件,比如有人点击了一个按钮。事实证明,这对于这种数值编程也非常有用——就像我只想要下一个数据批次。这意味着数据可以是任意长的,因为我们一次只获取一部分。我想简短的回答是因为这是 PyTorch 的工作方式。PyTorch 的数据加载器被设计为以这种方式调用。所以 Python 有这个生成器的概念,它是一种可以创建行为像迭代器的函数的方式。Python 已经认识到这种流处理编程方法非常方便和有用,并且在各处支持它。所以基本上任何你使用for ... in循环的地方,任何你使用列表推导的地方,这些东西都可以是生成器或迭代器。通过这种方式编程,我们获得了很大的灵活性。听起来对吗,Terrence?你是编程语言专家。
Terrence: 是的,我的意思是你说的很对。你可能会提到空间的问题,但在这种情况下,所有这些数据都必须在内存中,因为我们有…
Jeremy: 不需要在内存中。事实上,大多数情况下,使用 PyTorch,小批次将根据需要从分布在磁盘上的单独图像中读取,所以大多数情况下它不在内存中。
Terrence: 但一般来说,你希望尽可能少地一次性保存在内存中。所以流处理的想法也很棒,因为你可以进行组合。你可以将数据传送到另一台机器。
Jeremy: 是的,组合很棒。你可以从这里获取下一个东西,然后将其发送到下一个流中,然后你可以获取它并做其他事情。
Terrence: 你们都认识到,当然,在命令行管道和 I/O 重定向中。
Jeremy: 谢谢,Terrence。与真正知道自己在谈论什么的人一起工作的好处。
实现随机梯度下降[18:24]
现在让我们拿掉优化器。我们唯一剩下的是负对数似然损失函数,实际上我们也可以替换。我们在笔记本中有 Yannet 从头开始编写的实现。正如我们之前学到的那样,只需要一行代码。你可以用一个 if 语句来做到。所以我不知道为什么我如此懒惰,要包括这个。
所以我们要做的是,再次获取我们自己编写的模块(逻辑回归模块)。我们将再次进行一个 epoch。我们将循环遍历迭代器中的每个元素。我们将获取我们的独立和依赖变量用于小批量,将其传递给我们的网络,计算损失。所以这一切和以前一样,但现在我们要摆脱optimizer.step(),我们要手动做。所以基本的技巧是,正如我提到的,我们不会手动进行微积分。我们调用l.backward()来自动计算梯度,这将填充我们的矩阵。这就是我们构建的模块:

所以线性层权重的权重矩阵,我们称为l1_w,偏差我们称为l1_b。它们是我们创建的属性。所以我只是把它们放到了叫做w和b的东西里,基本上是为了节省一些输入。所以 w 是我们的权重,b 是我们的偏差。所以权重,记住权重是一个变量,要从变量中获取张量,我们必须使用.data。所以我们想要更新这个变量中的实际张量,所以我们说:
w.data -= w.grad.data * lr
-
-=我们想要朝着梯度的相反方向前进。梯度告诉我们哪个方向是向上的。我们想要向下。 -
w.grad.data * lr当前梯度乘以学习率。
这就是梯度下降的公式。正如你所看到的,这是你可能想象到的最简单的事情。就像更新权重等于它们现在的值减去梯度乘以学习率一样。对偏差也是同样的操作。
net2 = LogReg().cuda()
loss_fn=nn.NLLLoss()
lr = 1e-2
w,b = net2.l1_w,net2.l1_b
for epoch in range(1):
losses=[]
dl = iter(md.trn_dl)
for t in range(len(dl)):
xt, yt = next(dl)
y_pred = net2(V(xt))
l = loss(y_pred, Variable(yt).cuda())
losses.append(loss)
# Backward pass: compute gradient of the loss with respect
# to model parameters
l.backward()
w.data -= w.grad.data * lr
b.data -= b.grad.data * lr
w.grad.data.zero_()
b.grad.data.zero_()
val_dl = iter(md.val_dl)
val_scores = [score(*next(val_dl)) for i in range(len(val_dl))]
print(np.mean(val_scores))
问题:当我们在顶部执行next时,当循环结束时,我们如何获取下一个元素?所以这个(**for** t **in** range(len(dl)):)是在长度范围内的每个索引进行循环,所以这是 0、1、2…在这个循环结束时,它将打印出验证集的平均值,然后回到 epoch 的开始,在这一点上,它将创建一个新的迭代器。所以基本上在 Python 的后台当你调用iter(md.trn_dl)时,它基本上告诉它重置其状态以创建一个新的迭代器。如果你对它是如何工作感兴趣,所有的代码都可以供你查看。md.trn_dl是fastai.dataset.ModelDataLoader,所以我们可以看一下它的代码,看看它是如何构建的。所以你可以在这里看到,__next__函数跟踪了它在self.i中经历了多少次,这里是__iter__函数,当你创建一个新的迭代器时会调用这个函数。你可以看到它将其传递给另一个类型为 DataLoader 的东西,然后如果你对它是如何实现的感兴趣,你可以查看 DataLoader。

所以我们编写的 DataLoader 基本上使用多线程,允许同时进行多个操作。这非常简单。只有大约一屏的代码,所以如果你对简单的多线程编程感兴趣,这是一个值得一看的好东西。
问题:为什么你把这个包装在for epoch in range(1)中,因为这只会运行一次?因为在现实生活中,我们通常会运行多个 epochs。就像在这种情况下,因为这是一个线性模型,它实际上在一个 epoch 内训练到了它能达到的最好状态,所以如果我在这里输入 3,你会看到在第一个 epoch 之后它实际上不会有太大的改进。但当我们回到顶部时,我们将看一些稍微更深入和更有趣的版本,这将需要更多的 epochs。所以如果我要把这个转换成一个函数,我会像这样写def train_mdl,你会传入一些 epochs 的数量之类的东西。

要记住的一件事是,当你创建这些神经网络层时,记住这个(LogReg())在 PyTorch 看来只是一个 nn.Module ——我们可以将其用作一个层,我们可以将其用作一个函数,我们可以将其用作一个神经网络。PyTorch 不认为这些是不同的东西。因此,这可能是另一个网络中的一层。那么梯度是如何工作的呢?所以如果你有一个层,我们可以将其看作是激活或通过某些其他非线性/线性激活函数计算出的一些激活。然后从该层,很可能我们会将其通过矩阵乘积来创建一些新层。因此,如果我们抓取像这样的一个激活,实际上会用来计算每一个输出。

因此,如果要计算导数,你必须知道这个权重矩阵如何影响每个输出,并将所有这些加在一起以找到一个激活在所有输出上的总影响。这就是为什么在 PyTorch 中你必须告诉它何时将梯度设置为零。因为想法是你可能有很多不同的损失函数或者下一组激活中的很多不同的输出,所有这些都会增加或减少你的梯度。所以你基本上必须说,好的,这是一个新的计算 — 重置。所以这就是我们这样做的地方:

在我们执行l.backward()之前,我们说重置。所以让我们拿出我们的权重,拿出梯度,拿出它们指向的张量,然后zero_。在 PyTorch 中,下划线作为后缀意味着“原地”,听起来像一个小技术细节,但记住这一点非常有用。几乎每个函数都有一个下划线版本的后缀,它会原地执行操作。所以通常 zero 返回一个特定大小的零张量,所以 zero_ 意味着用一堆零替换这个内容。
好了,就是这样。这就是从头开始的 SGD。如果我去掉我的菜单栏,我们可以正式说它适合在一个屏幕内。当然,我们还没有得到我们的逻辑回归的定义,那是另外半个屏幕,但基本上没有太多内容。
问题:为什么我们需要多个 epochs?简单回答就是,假设我们的学习率很小。那么它就不会走得很远。没有什么规定说通过一个 epoch 就足以让你达到目标。所以这就像是,好吧,让我们增加学习率。当然,我们可以增加学习率,但谁能说最高的学习率是稳定学习的足够多呢。对于大多数数据集和大多数架构来说,一个 epoch 很少能让你达到最好的结果。线性模型的行为非常好。所以你通常可以使用更高的学习率并更快地学习。此外,通常无法获得如此好的准确性,因此也没有太多的提升空间。因此,进行一个 epoch 将是罕见的。
向后走
让我们往回走。所以往回走,我们基本上会说让我们不要一遍又一遍地写这些代码(在左侧)。让别人替我们做。


这些版本之间唯一的区别就是,不是我们自己说.zero_或-= gradient * lr,而是这些操作已经为我们封装好了(在右侧)。
这里还有一个问题,即左侧更新权重的方法实际上效率很低。它没有利用动量和曲率。因此,在深度学习课程中,我们也学习了如何从头开始实现动量。因此,如果我们实际上只是使用普通的 SGD 而不是 Adam,它们实际上是完全相同的,你会看到左侧版本学习得更慢。
让我们自动做更多的事情。考虑到每次训练时,我们必须循环遍历 epoch、batch,进行前向传播,计算损失,梯度清零,反向传播,优化器进行一步操作,让我们把所有这些放在一个函数中。这个函数被称为fit:

就是这样。让我们看看 fit:

然后这是步骤:

梯度清零,计算损失(记住,PyTorch 倾向于称之为准则而不是损失),进行反向传播。然后,还有一些我们在这里没有学到的东西,但我们在深度学习课程中学到的,那就是“梯度裁剪”,所以你可以忽略它。所以你可以看到,我们学到的所有东西,当你查看实际框架内部时,那就是你看到的代码。这就是 fit 的作用。
然后下一步就是有一些权重和偏差,进行矩阵乘法和加法,让我们把它放在一个函数中。进行对数 softmax 的操作,让我们把它放在一个函数中。然后首先进行这个操作,然后进行那个操作,将函数链接在一起的想法,让我们把它放在一个函数中。最终我们得到了:

所以 Sequential 简单地意味着通过这个函数执行这个操作,将结果传递给这个函数,依此类推。而 Linear 意味着创建权重矩阵,创建偏差。就是这样。
然后,正如我们开始讨论的那样,通过将其放入 100 个激活中,而不是直接将其发送到 10 个激活中,我们可以将其转换为一个深度神经网络。我们可以选择任何我们喜欢的数字。通过 ReLU 使其非线性化,通过另一个线性层,再通过一个 ReLU,然后通过我们的最终输出和最终激活函数。

现在这是一个深度网络。所以我们可以拟合它。这一次,因为它更深了,我实际上要运行更多的 epochs。你可以看到准确性在增加:

如果你尝试将学习率从 0.1 进一步增加,它实际上开始变得不稳定。
学习率退火
我会告诉你一个技巧。这被称为学习率退火,技巧就是这样。当你试图拟合一个函数时,你已经走了几步。当你接近底部时,你的步伐可能会变得更小。否则,通常会发生的情况是你发现自己在同样的地方来回摆动。

你可以在上面的准确性中实际看到它开始变得平坦。这可能是因为它已经做得尽可能好了,或者可能是因为它在前进和后退。所以在训练后期降低学习率并采取更小的步骤是个好主意。这就是所谓的学习率退火。在 Fast AI 中有一个名为set_lrs(设置学习率)的函数,你可以传入你的优化器和新的学习率,看看是否有帮助。很多时候确实有帮助。你应该减少大约一个数量级。在深度学习课程中,我们学习了一种比这更好的技术,可以自动进行学习率退火并在更细粒度的级别上进行。但如果你手动操作,一次减少一个数量级是人们通常做的事情。

你会看到论文中谈论学习率调度,这就像一个学习率调度。这个调度让我们达到了 97%。我尝试继续下去,但似乎我们无法比这更好。所以我们得到了一个可以达到 97%准确性的东西。
问题:我有一个关于数据加载的问题。我知道这是一个 Fast AI 函数,但你能详细介绍一下它是如何创建批次的,如何完成的,以及如何做出这些决定吗?当然。基本上,PyTorch 中有一个非常好的设计,他们基本上说让我们创建一个叫做数据集的东西。数据集基本上看起来像一个列表。它有一个长度(例如数据集中有多少图像),并且可以像列表一样进行索引。所以如果你有数据集d,你可以这样做:
d = Dataset(...)
len(d)
d[i]
这基本上就是 PyTorch 关心的数据集。所以你从数据集开始,就像d[3]给你第三张图像,等等。所以你拿一个数据集,你可以把它传递给一个数据加载器的构造函数dl = DataLoader(d)。这会给你一个现在可迭代的东西。所以你现在可以说iter(dl),这是你可以调用 next 的东西(即next(iter(dl)))。当你调用数据加载器的构造函数时,你可以选择打开或关闭洗牌。打开洗牌意味着给我随机的小批量,关闭洗牌意味着按顺序进行。所以当你调用next时,假设你说shuffle=True并且批量大小是 64,它会在 0 到长度之间抓取 64 个随机整数,并调用这个(d[i])64 次以获取 64 个不同的项目并将它们组合在一起。所以 Fast AI 使用完全相同的术语和完全相同的 API。我们只是以不同的方式处理一些细节。特别是在计算机视觉中,你经常想要做很多数据增强,比如翻转、稍微改变颜色、旋转,这些都是计算密集型的。甚至只是读取 JPEG 文件也是计算密集型的。所以 PyTorch 使用一种方法,即启动多个处理器并行进行处理,而 Fast AI 库则使用一种称为多线程的方法,这可能是更快的方法。
问题:在“epoch”中,所有元素都会被返回一次吗?是在 epoch 开始时进行洗牌吗?是的,并非所有库都以相同的方式工作。有些会进行有放回抽样,有些则不会。Fast AI 库实际上将洗牌交给了实际的 PyTorch 版本,我相信 PyTorch 版本实际上会进行洗牌,一个 epoch 会覆盖所有元素,我相信。
现在问题是,当你开始使用这些更大的网络时,潜在地你会得到相当多的参数。我想要求你计算一下有多少参数,但让我们记住这里我们有 28 乘以 28 的输入进入 100 个输出,100 进入 10。然后对于每一个,我们有权重和偏置。

所以我们实际上可以这样做。net.parameters返回一个列表,列表中的每个元素都是一个包含参数的张量,不仅仅是那一层,如果是一个既有权重又有偏置的层,那就是两个参数。所以基本上给我们返回了一个包含所有参数的张量的列表。PyTorch 中的numel告诉你它有多大。

所以如果我运行这个,这里是每一层中的参数数量。所以我有 784 个输入,第一层有 100 个输出,因此第一个权重矩阵的大小是 78400。第一个偏置向量的大小是 100。然后下一个是 100 乘以 100,有 100。然后下一个是 100 乘以 10,10 是偏置。所以每一层中的元素数量就是这样。我把它们加起来,差不多有十万个。所以我可能有过拟合的风险。所以我们可能需要考虑使用正则化。
正则化
在所有机器学习中,一种非常简单常见的正则化方法叫做 L2 正则化。这非常重要,非常方便,你可以将它用于几乎任何东西。基本思想是这样的。通常我们会说我们的损失等于(让我们用 RMSE 来保持简单)我们的预测减去我们的实际值的平方,然后求和,取平均值,再开平方。

如果我们想说,如果我有很多参数,除非它们真的足够有用,否则不要使用它们。如果你有一百万个参数,而你只真正需要 10 个参数来有用,那就只用 10 个。那么我们如何告诉损失函数做到这一点呢?基本上我们想说的是,嘿,如果一个参数是零,那没问题。就好像它根本不存在一样。所以让我们惩罚一个参数不为零。我们如何衡量这一点呢?我们如何计算我们的参数有多不为零?L1 是权重平均值的绝对值。L2 是权重本身的平方。然后我们想要说好,我们想要惩罚不为零的程度有多大?因为如果我们实际上没有那么多参数,我们根本不想要进行正则化。如果我们有很多参数,我们确实想要进行大量正则化。所以我们加入一个参数 a:

除了可能打印出来之外,我们实际上并不关心损失。我们真正关心的是损失的梯度。aw²的梯度是2aw。所以有两种方法可以做到这一点:
-
我们实际上可以修改我们的损失函数来添加这个平方惩罚。
-
我们可以修改我们说的权重等于权重减去梯度乘以学习率的那个东西,也加上2aw。
这些基本上是等价的,但它们有不同的名称。第一个称为 L2 正则化,第二个称为权重衰减。第一个版本是最初在神经网络文献中提出的,而第二个版本是在统计文献中提出的,它们是等价的。
正如我们在深度学习课程中讨论的那样,事实证明它们并不完全等价,因为当你有动量和 Adam 等因素时,它们的行为可能会有所不同。两周前,一位研究人员找到了一种方法来在现代优化器中实现正确的权重衰减,我们 Fast AI 的一位学生在 Fast AI 库中实现了这一点,因此 Fast AI 现在是第一个实际支持这一功能的库。
无论如何,现在让我们使用 PyTorch 称为权重衰减的版本,但实际上根据两周前的这篇论文,它实际上是 L2 正则化。这并不完全正确,但足够接近。所以在这里,我们可以说权重衰减是 1e-3。

这将把我们的惩罚乘数 a 设置为 1e-3,并将其添加到损失函数中。让我们复制这些单元格,以便我们可以比较它们的训练方式。你可能会注意到这里有一些反直觉的地方[48:54]。0.23547 是我们的训练误差。你可能会期望我们的带有正则化的训练误差会更糟,因为我们正在惩罚那些可以使其更好的参数。然而实际上,它开始时并不是更糟(之前是 0.29756)。这可能是为什么呢?

这样做的原因是,如果你有一个看起来像这样的函数:

训练可能需要很长时间,否则,如果你有一个看起来更像这样的函数:

它会训练得更快。有些事情你可以做,有时只是可以让一个可怕的函数变得不那么可怕。有时候权重衰减实际上可以使你的函数行为更好,这实际上在这里发生了。所以我只是提到这一点是为了说不要让这使你困惑。权重衰减确实对训练集进行惩罚,严格来说,我们最终得到的训练集的数字不应该更好,但有时候它可以更快地训练。
问题:我不明白。为什么会使它更快?训练时间重要吗?不,这是在一个时代之后。底部是我们没有使用权重衰减的训练,顶部是使用了权重衰减的训练。这与时间无关,只与一个时代有关。在一个时代之后,我的观点是,所有其他条件相同,你会预期使用权重衰减的训练集会有更糟的损失,因为我们在惩罚它。我说“哦,不是这样。这很奇怪。”

原因在于,在一个单独的时代中,重要的是你是在尝试优化一个非常崎岖的东西,还是在尝试优化一个平滑的东西。如果你试图优化一个非常崎岖的东西,想象一下在某个高维空间中,你最终会在所有这些不同的管道和隧道中滚动。而如果它只是平滑的,你只是一下就到了。想象一颗大理石滚下山坡,其中一个是旧金山的隆巴德街 - 前进,后退,前进,后退,需要很长时间才能开到尽头。而如果你骑摩托车直接越过山顶,速度就快得多。因此,损失函数表面的形状定义了优化的难易程度。因此,根据这些结果,似乎在这里使用权重衰减使得这个函数更容易优化。
问题:所以只是为了确保,惩罚会使优化器更有可能达到全局最小值吗?不,我不会这么说。我的观点实际上是,最终,它可能在训练集上表现得不太好,确实看起来是这样。最终,在五个时代之后,我们的训练集现在比使用权重衰减时更糟糕。这是我所期望的。就像我从不使用全局最优这个术语,因为我们对此没有任何保证。我们并不真正关心。我们只关心在经过一定数量的时代之后我们到达了哪里。我们希望我们找到了一个好的解决方案。因此,当我们达到一个好的解决方案时,使用权重衰减的训练集,损失更糟糕,因为它是惩罚。但在验证集上,损失更好,因为我们对训练集进行了惩罚,以便尝试创建一个更好泛化的东西。因此,无用的参数现在为零,泛化更好。所以我们所说的只是在一个时代之后它达到了一个好的点。
问题:这总是真的吗?如果你的意思是权重衰减总是使函数表面更加平滑,那么不,这并不总是真的。但值得记住,如果你在训练一个函数时遇到困难,添加一点点权重衰减可能会有所帮助。
问题:通过对参数进行正则化,它的作用是使损失函数表面变得更加平滑?我的意思是,这不是我们这样做的原因。我们这样做的原因是因为我们想惩罚那些不为零的东西,告诉它不要让这个参数变得很大,除非它真的对损失有很大帮助。如果可以的话,将其设置为零,因为将尽可能多的参数设置为零意味着它会更好地泛化。这就像拥有一个更小的网络一样。这就是我们这样做的原因。但它也可以改变学习方式。
我想检查一下我们实际上在这里是怎么做的。所以在第二个时代之后,你可以看到这里确实有帮助。在第二个时代之后,我们之前达到了 97%的准确率,现在我们几乎达到了 98%的准确率。你可以看到损失是 0.08 对 0.13。所以添加正则化使我们能够找到更好的解决方案(3%对 2%)。

问题:所以这有两个部分——一个是 L2 正则化和权重衰减?不,我的观点是它们是同一件事。所以权重衰减是 L2 正则化的版本,如果你只是对 L2 正则化求导,你会得到权重衰减。所以你可以通过改变损失函数来实现它,加入平方损失惩罚,或者你可以通过将权重本身添加到梯度中来实现它。
问题:我们可以在卷积层中使用正则化吗?当然可以。卷积层只是权重。
问题:你能解释一下为什么你认为在这个特定问题中需要权重衰减吗?不容易。我是说,除了说这是我总是会尝试的事情之外。继续提问:过拟合?所以如果我的训练损失高于验证损失,那么我就是欠拟合。所以肯定没有必要正则化。那总是不好的。那总是意味着你的模型需要更多的参数。在这种情况下,我是过拟合的。这并不一定意味着正则化会有帮助,但值得一试。

问题:你如何选择最佳的时代数?你参加我的深度学习课程😆 这是一个很长的故事。我们没有时间在这堂课上讨论最佳实践。我们将学习基础知识。
现代机器学习技术的秘密
在深度学习课程中我们详细讨论的一点是,我认为现代机器学习技术的秘密是对问题的解决方案进行大规模的参数化,就像我们刚刚做的那样。当我们只有少量的 28x28 图像时,我们有大约 10 万个权重,然后使用正则化。这与几十年前几乎所有统计和学习的做法完全相反,大多数大学的大多数领域的高级讲师仍然具有这种背景,他们学习到构建模型的正确方式是尽可能少地使用参数。因此,希望我们迄今已经学到了两件事。一是即使模型有很多参数,我们也可以构建非常准确的模型。随机森林有很多参数,这里的深度网络也有很多参数,它们可以很准确。我们可以通过使用装袋或使用正则化来实现。在神经网络中,正则化意味着权重衰减(也称为“某种程度的” L2 正则化)或者我们在这里不会过多担心的 dropout。这是一种构建有用模型的非常不同的思考方式。我只是想警告你,一旦你离开这个教室,甚至可能当你去听下一个教员的讲座时,甚至在美国旧金山大学也会有完全受过小参数模型训练的人。你的下一个老板可能是在小参数模型的世界中接受过培训的。他们认为这些模型在某种程度上更纯净、更容易、更好、更可解释或者其他什么。我相信这不是真的 - 可能永远不是真的。当然很少是真的。实际上,正如我们从随机森林解释的整个课程中学到的那样,具有大量参数的模型可以非常可解释。你可以使用大部分相同的技术来处理神经网络,但是神经网络更容易。记得我们是如何通过随机化一列来计算特征重要性的吗,以查看该列的变化如何影响输出?嗯,这就像一种愚蠢的计算梯度的方式。改变这个输入会如何改变输出?对于神经网络,我们实际上可以计算其梯度。因此,使用 PyTorch,你实际上可以说输出相对于这一列的梯度是多少?你可以使用相同的方法来使用神经网络进行偏依赖图。对于那些对产生真正影响感兴趣的人,基本上没有人为神经网络编写这些东西。因此,整个领域需要编写库、撰写博客文章。一些论文已经写了,但只在非常狭窄的领域,比如计算机视觉。据我所知,没有人写过关于如何进行结构化数据神经网络解释方法的论文。因此,这是一个非常令人兴奋的大领域。
NLP [1:02:04]
然而,我们将从应用简单的线性模型开始。对我来说有点可怕,因为我们将进行 NLP,而我们的 NLP 专家就在房间里。因此,如果我搞砸了,David,请大声告诉我。NLP 指的是我们处理自然语言文本的任何建模。有趣的是,我们将看一个情况,线性模型在解决特定问题时非常接近最先进技术。几周前,我实际上使用递归神经网络超越了最先进技术,但这实际上将向你展示线性模型非常接近最先进技术。
IMDb
笔记本
我们将使用 IMDb 数据集。这是一个电影评论数据集。您可以按照以下步骤下载它:
To get the dataset, in your terminal run the following commands:wget http://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gzgunzip aclImdb_v1.tar.gztar -xvf aclImdb_v1.tar
一旦你下载了它,你会看到你有一个训练和一个测试目录,在你的训练目录中,你会看到有一个负面和一个正面目录。在你的正面目录中,你会看到有一堆文本文件。
PATH='data/aclImdb/'
names = ['neg','pos']
%ls {PATH}
'''
aclImdb_v1.tar.gz imdbEr.txt imdb.vocab models/ README test/ tmp/ train/
'''
%ls {PATH}train
'''
aclImdb/ all_val/ neg/ tmp/ unsupBow.feat urls_pos.txt
all/ labeledBow.feat pos/ unsup/ urls_neg.txt urls_unsup.txt
'''
%ls {PATH}train/pos | head
'''
0_9.txt
10000_8.txt
10001_10.txt
10002_7.txt
10003_8.txt
10004_8.txt
10005_7.txt
10006_7.txt
10007_7.txt
10008_7.txt
...
'''
这里是一个文本文件的例子:
trn[0]
'''
"Story of a man who has unnatural feelings for a pig. Starts out with a opening scene that is a terrific example of absurd comedy. A formal orchestra audience is turned into an insane, violent mob by the crazy chantings of it's singers. Unfortunately it stays absurd the WHOLE time with no general narrative eventually making it just too off putting. Even those from the era should be turned off. The cryptic dialogue would make Shakespeare seem easy to a third grader. On a technical level it's better than you might think with some good cinematography by future great Vilmos Zsigmond. Future stars Sally Kirkland and Frederic Forrest can be seen briefly."
'''
所以我们不知何故选出了一个男人对猪有不自然感情的故事作为我们的第一个选择。这并不是故意的,但没关系。
我们将查看这些电影评论,对于每一个,我们将查看它们是积极的还是消极的。所以它们被放入了其中一个文件夹。它们是从 IMDb(电影数据库和评论网站)下载的。那些非常积极的评论放在/pos中,非常消极的评论放在/neg中,而其余的则没有标签(/unsup)。所以只有高度极化的评论。
所以在上面的例子中,我们有一个疯狂的暴力暴民,不幸的是太荒谬了,太令人反感了,那些来自那个时代的人应该被关掉。所以这个的标签是零,即负面的,所以这是一个负面的评论。
trn_y[0]
'''
0
'''
在 Fast AI 库中,有很多函数和类可以帮助你处理大多数机器学习的领域。对于自然语言处理,我们有一个简单的东西,就是来自文件夹的文本。
trn,trn_y = texts_labels_from_folders(f'{PATH}train',names)
val,val_y = texts_labels_from_folders(f'{PATH}test',names)
这将遍历并找到这里的所有文件夹(第一个参数f'{PATH}train')与这些名称(第二个参数names)并创建一个带标签的数据集。不要让这些事情阻止你理解幕后发生的事情。我们可以获取它的源代码,你会看到它很小,就像 5 行。

我不喜欢把这些东西写得很详细,而是把它们隐藏在一些小函数后面,这样你就可以重复使用它们。但基本上,它将遍历每个目录,遍历该目录中的每个文件,然后将其放入一个文本数组中,找出它在哪个文件夹中,并将其放入一个标签数组中。这就是我们最终得到的东西,我们有一个评论数组和一个标签数组。
这就是我们的数据。所以我们的工作将是接受一部电影评论并预测标签。我们将要做的是,我们将丢弃关于语言的所有有趣的东西,即单词的顺序。这通常不是一个好主意,但在这种情况下,它将不会太糟糕。所以让我告诉你我所说的丢弃单词顺序是什么意思。通常,单词的顺序非常重要。如果你在某个单词前面有一个“not”,那么这个“not”就指的是那个东西。但在这种情况下,我们试图预测某物是积极的还是消极的。如果你看到“荒谬”或“神秘”这样的词经常出现,也许这是一个迹象表明这不是很好。所以我们的想法是将其转换为一个称为术语文档矩阵的东西,对于每个文档(即每个评论),我们只是创建一个包含其中的单词列表,而不是它们的顺序。
术语文档矩阵示例:
朴素贝叶斯.xlsx

这里有四个我编造的电影评论。所以我将把这些转换成一个术语文档矩阵。我需要做的第一件事是创建一个称为词汇表的东西。词汇表是出现的所有唯一单词的列表。这是我的词汇表:this, movie, is, good, the bad。这就是所有的单词。现在我将把我的每个电影评论转换成一个向量,显示哪些单词出现以及它们出现的频率。在这种情况下,我的单词没有出现两次。所以这被称为术语文档矩阵:

这种表示法,我们称之为词袋表示法。所以这里是评论的一个词袋表示。

它不再包含文本的顺序。它只是一袋词(即其中包含哪些词)。它包含“bad”,“is”,“movie”,“this”。所以我们要做的第一件事是将其转换为一种词袋表示。这对于线性模型来说很方便的原因是,这是一个我们可以进行数学运算的漂亮矩阵。具体来说,我们可以进行逻辑回归,这就是我们要做的。我们将达到一个进行逻辑回归的点。不过,在那之前,我们将做另一件事,那就是朴素贝叶斯。sklearn 有一个可以为我们创建术语文档矩阵的东西,叫做CountVectorizer,所以我们将使用它。
标记化 [1:09:01]
现在在自然语言处理中,你必须将文本转换为单词列表,这就是所谓的标记化。这实际上并不是微不足道的,因为如果这实际上是This movie is good.或This “movie” is good.,你如何处理标点符号呢?更有趣的是,如果这是This "movie" isn’t good.,你如何将一段文本转换为标记列表呢?一个好的标记器会将这个转换为:
之前:This "movie" isn’t good.
之后:This " movie " is n’t good .
所以你可以看到,在这个版本中,如果我现在按空格分割这个文本,每个标记要么是一个单独的标点符号,要么是这个后缀n't,被视为一个单词。这就是我们可能想要对这段文本进行标记化的方式,因为你不希望good.成为一个对象。没有good.或"movie"是一个对象的概念。所以标记化是我们交给标记器的事情。Fast AI 中有一个我们可以使用的标记器,这就是我们如何使用标记器创建我们的术语文档矩阵:
veczr = CountVectorizer(tokenizer=tokenize)
sklearn 有一个相当标准的 API,这很好。我相信你以前见过几次。一旦我们建立了某种“模型”,我们可以把CountVectorizer看作是一种模型,这只是定义它将要做什么。我们可以调用fit_transform来执行这个操作。
trn_term_doc = veczr.fit_transform(trn)
val_term_doc = veczr.transform(val)
在这种情况下,fit_transform将创建词汇表,并基于训练集创建术语文档矩阵。transform有点不同。它表示使用先前拟合的模型,这在这种情况下意味着使用先前创建的词汇表。我们不希望验证集和训练集在矩阵中有不同顺序的单词。因为那样它们会有不同的含义。所以这里说的是使用相同的词汇表为验证集创建一个词袋。
问题:如果验证集中有不同于训练集的单词集合怎么办[1:11:40]?这是一个很好的问题。通常,大多数这些词汇创建方法会为未知单词设定一个特殊标记。有时你也可以说,如果一个单词出现少于三次,就称之为未知。但是,如果你看到了以前没有见过的东西,就称之为未知。所以(即“未知”)只会成为词袋中的一列。
当我们创建这个术语文档矩阵时,训练集有 25,000 行,因为有 25,000 条电影评论,有 75,132 列,这是唯一单词的数量。
trn_term_doc
'''
<25000x75132 sparse matrix of type '<class 'numpy.int64'>'
with 3749745 stored elements in Compressed Sparse Row format>
'''
现在,大多数文档并不包含这 75,132 个单词中的大部分。所以我们不想把它实际存储为内存中的普通数组。因为这样会非常浪费。所以,我们将其存储为稀疏矩阵。稀疏矩阵的作用是将其存储为一种只指示非零值位置的东西。所以它会说,文档编号 1,单词编号 4 出现了 4 次。文档编号 1,术语编号 123 出现了一次,依此类推。
(1, 4) → 4
(1, 123) → 1
这基本上就是它的存储方式。实际上有许多不同的存储方式,如果你学习 Rachel 的计算线性代数课程,你将了解不同类型的存储方式以及为什么选择它们,如何转换等等。但它们都类似于这样,你不需要太担心细节。重要的是它是高效的。
所以我们可以拿到第一条评论,这给了我们一个 75,000 个长稀疏的一行长矩阵,其中有 93 个存储元素。换句话说,这些单词中有 93 个实际上在第一个文档中使用。
trn_term_doc[0]
'''
<1x75132 sparse matrix of type '<class 'numpy.int64'>'
with 93 stored elements in Compressed Sparse Row format>
'''
我们可以通过说veczr.get_feature_names来查看词汇表,这给我们提供了词汇表。这里是一些特征名称的元素的示例:
vocab = veczr.get_feature_names(); vocab[5000:5005]
'''
['aussie', 'aussies', 'austen', 'austeniana', 'austens']
'''
我并没有故意选择那个有澳大利亚的,但那是重要的单词,显然😄我这里没有使用分词器。我只是按空格分割,所以这与矢量化器所做的不完全相同。但为了简化事情,让我们拿到所有小写单词的集合。通过将其设置为集合,我们使它们成为唯一的。所以这大致是可能出现的单词列表。
w0 = set([o.lower() for o in trn[0].split(' ')]); w0
'''
{'a',
'absurd',
'an',
'and',
'audience',
'be',
'better',
'briefly.',
'by',
'can',
...
}
'''
len(w0)
'''
91
'''
这个长度是 91,与 93 相似,唯一的区别是我没有使用真正的分词器。所以基本上就是这样。创建了这个唯一的单词列表并将它们映射。我们可以通过调用veczr.vocabulary_来查找特定单词的 ID。所以这就像veczr.get_feature_names的反向映射,它将整数映射到单词,veczr.vocabulary_将单词映射到整数。
veczr.vocabulary_['absurd']
'''
1297
'''
所以我们看到“荒谬”在第一个文档中出现了两次,所以让我们检查一下:
trn_term_doc[0,1297]
'''
2
'''
这就是,这是 2。否则,不幸的是,澳大利亚人没有出现在与猪有不自然关系的电影中,所以这是零:
trn_term_doc[0,5000]
'''
0
'''
这就是我们的术语文档矩阵。
问题:它是否关心单词之间的关系,比如单词的顺序?不,我们抛弃了顺序。这就是为什么它是一个词袋。我并不是在声称这一定是一个好主意。我要说的是,在过去几十年里进行的绝大多数自然语言处理工作通常使用这种表示,因为我们并不真正知道更好的方法。如今,我们越来越多地使用递归神经网络,我们将在第 1 部分的最后一个深度学习课程中学习。但有时这种表示方法效果还不错,实际上在这种情况下也会效果不错。
事实上,当我在我的电子邮件公司 FastMail 时,我们做的很多垃圾邮件过滤都使用了下一个技术朴素贝叶斯,这是一种词袋方法。如果你收到很多包含“伟哥”一词的电子邮件,而且它们一直是垃圾邮件,你从来没有收到朋友谈论“伟哥”的电子邮件,那么很可能说“伟哥”的东西无论语言的细节如何,都可能来自垃圾邮件发送者。所以这就是使用术语文档矩阵进行分类的基本理论。
朴素贝叶斯
让我们来谈谈朴素贝叶斯。这里是基本思想。我们将从我们的术语文档矩阵开始。前两个是我们的正面评论语料库。接下来两个是我们的负面评论语料库。所以这里是我们所有评论的整个语料库:

我们倾向于更通用地称这些列为“特征”而不是“单词”。this是一个特征,movie是一个特征,等等。所以现在更像是机器学习语言。一列是一个特征。在朴素贝叶斯中我们称这些为f。所以我们基本上可以说,给定类别为 1 时你会看到单词this的概率(即积极评论)就是你在积极评论中看到this的频率的平均值。现在我们必须要小心一点,因为如果你在某个类别中从未看到某个单词,所以如果我从未收到过朋友发来的提到“伟哥”的电子邮件,这并不意味着朋友给我发送有关伟哥的电子邮件的概率是零。实际上并不是零。我希望明天不会收到 Terrence 发来的电子邮件,说“Jeremy,你可能需要这个关于伟哥的广告”,但这种情况可能发生。我相信这对我有利🤣所以我们说实际上到目前为止我们看到的并不是所有可能发生的一切的完整样本。这更像是迄今为止发生的事情的样本。所以让我们假设你接下来收到的电子邮件实际上提到了伟哥和其他所有可能的单词。所以基本上我们要添加一行 1。

就像包含每个可能单词的电子邮件一样。这样,没有什么是无限不可能的。所以我取我积极语料库中所有this出现的平均次数再加上 1:

所以这就像是在文档中feature = 'this'出现的概率,假设class = 1(即this的p(f|1))。
毫不奇怪,这里是相同的概率,即给定class = 0时出现this的概率:

相同的计算,只是对于零行。显然这些是相同的,因为this在积极评论中出现一次,在消极评论中也出现一次。
我们可以为每个特征的每个类别做同样的计算[1:20:40]

所以我们现在的技巧基本上是使用贝叶斯规则来填充这个。所以我们想要的是在给定这个特定文档的情况下(所以有人给我发送了这封特定的电子邮件,或者我有这个特定的 IMDb 评论),其类别等于积极的概率是多少。所以对于这个特定的电影评论,它的类别是积极的概率是多少。所以我们可以说,嗯,这等于我们得到这个特定电影评论的概率,假设它的类别是积极的,乘以任何电影评论的类别是积极的概率除以得到这个特定电影评论的概率。

这就是贝叶斯规则。所以我们可以计算所有这些东西,但实际上我们真正想知道的是这是类别 0 还是类别 1 更有可能。如果我们实际上计算了类别 1 的概率并除以类别 0 的概率会怎样呢?

好的,如果这个数字大于 1,那么更有可能是类别 1,如果小于 1,更有可能是类别 0。所以在这种情况下,我们可以将整个事情除以类别 0 的相同版本,这等同于乘以倒数。所以好处是现在*p(d)*被取消了,下面是给定类别 0 时得到数据的概率,这里是得到类别 0 的概率。

基本上这意味着我们想要计算的是在类别为 1 的情况下得到这个特定文档的概率乘以类别为 1 的概率除以在类别为 0 的情况下得到这个特定文档的概率乘以类别为 0 的概率:

所以类别为 1 的概率就等于标签的平均值[1:23:20]。类别为 0 的概率是 1 减去那个值。所以有这两个数字:

我有相同数量的两者,所以都是 0.5。
如果这个文档的类别是 1,获得这个文档的概率是多少?学生:看看所有类别等于 1 的文档,1 除以那个会给你……[1:24:02] Jeremy: 所以记住这将是针对特定文档的。例如,会说这个评论是积极的概率是多少。所以你走在正确的轨道上,但我们要做的是看看它包含的单词,然后将类别等于 1 的概率相乘在一起。所以类别 1 的评论包含this的概率是 2/3,包含movie的概率是 1,is是 1,good是 1。所以它包含所有这些的概率是所有这些相乘在一起。有点。Tyler,为什么不是真的?所以很高兴你看起来震惊和怀疑 😄
Tyler: 选择不是独立的吗?
Jeremy: 谢谢。所以没有人能说 Tyler 天真,因为这是朴素贝叶斯的原因,因为这是如果你以朴素的方式使用贝叶斯定理会发生的事情。而 Tyler 并不天真。完全不是。所以朴素贝叶斯说让我们假设如果你有“这部电影太愚蠢了,我讨厌它”但讨厌的概率独立于愚蠢的概率独立于愚蠢的概率,这显然是不正确的。所以朴素贝叶斯实际上并不是很好,但我教给你们是因为它将成为我们即将学习的某些东西的便利工具。背景: 而且它通常效果还不错。Jeremy: 还好。我的意思是我永远不会选择它。我不认为它比任何其他同样快速和同样简单的技术更好。但这是你可以做的事情,肯定会成为有用的基础。
所以现在这是计算我们得到这个特定文档的概率,假设它是一个积极的评论[1:26:08]:

这是给定它是负面的概率

这里是比率。比率大于 1,所以我们将说我们认为这可能是一个积极的评论。

这就是 Excel 版本。所以你可以看出我让 Yannet 来处理这个,因为里面有 LaTeX。我们有实际的数学。所以这里是相同的东西;每个特征f的对数计数比。

所以这是用 Python 写出来的。我们的自变量是我们的术语文档矩阵,我们的因变量只是y的标签。所以使用 numpy,这个x[y==1]将抓取因变量为 1 的行。然后我们可以对行求和,以获得该特征在所有文档中的总词数,再加 1 — Terrence 今天肯定会给我发关于伟哥的东西,我能感觉到。就是这样。然后对负面评论做同样的事情。然后当然最好取对数,因为如果我们取对数,那么我们可以将事物相加而不是相乘。一旦你将足够多的这些东西相乘在一起,它将接近零,你可能会用完浮点数。所以我们取这些比率的对数。然后,正如我所说的,我们将将其相乘,或者用对数,将其加到整个类别概率的比率上。
def pr(y_i):
p = x[y==y_i].sum(0)
return (p+1) / ((y==y_i).sum()+1)
x=trn_term_doc
y=trn_yp = x[y==1].sum(0)+1
q = x[y==0].sum(0)+1
r = np.log((p/p.sum())/(q/q.sum()))
b = np.log(len(p)/len(q))
为了对每个文档说,将贝叶斯概率乘以计数,我们可以使用矩阵乘法。然后添加类别比率的对数,你可以使用+ b。所以我们最终得到的东西看起来很像逻辑回归。但我们并没有学到任何东西。不是从 SGD 的角度来看。我们只是使用这个理论模型进行计算。正如我所说,我们可以将其与零进行比较,看看它是更大还是更小 — 不再是 1,因为我们现在处于对数空间。然后我们可以将其与均值进行比较。这样的准确率约为 81%。所以朴素贝叶斯并不是没有用的。它给了我们一些东西。
pre_preds = val_term_doc @ r.T + b
preds = pre_preds.T>0
(preds==val_y).mean()
'''
0.80691999999999997
'''
事实证明,这个版本实际上是在看 a 出现的频率,比如“荒谬”出现了两次,至少对于这个问题来说,通常无论“荒谬”出现了两次还是一次都无关紧要[1:29:03]。重要的是它出现了。所以人们倾向于尝试的是取术语矩阵文档并使用.sign(),它会将任何正数替换为1,将任何负数替换为-1(显然我们没有负计数)。这样就实现了二值化。它表示我不在乎你看到“荒谬”两次,我只在乎你看到它。所以如果我们对二值化版本做完全相同的事情,那么结果会更好。
pre_preds = val_term_doc.sign() @ r.T + b
preds = pre_preds.T>0
(preds==val_y).mean()
'''
0.82623999999999997
'''
逻辑回归[1:30:01]
现在这就是理论和实践之间的区别。理论上,朴素贝叶斯听起来还可以,但是它是朴素的,不像泰勒,它是朴素的。所以泰勒可能会说,与其假设我应该使用这些系数r,为什么不让我们学习它们呢?所以让我们学习它们。我们完全可以学习它们。
那么让我们创建一个逻辑回归,并拟合一些系数。这实际上会给我们提供与之前完全相同的功能形式,但现在我们不再使用理论上的r和理论上的b,而是根据逻辑回归计算这两个值。这样更好。
m = LogisticRegression(C=1e8, dual=True)
m.fit(x, y)
preds = m.predict(val_term_doc)
(preds==val_y).mean()
'''
0.85504000000000002
'''
所以这有点像是,为什么要基于某种理论模型进行某些操作呢?因为理论模型几乎永远不会像数据驱动模型那样准确。因为理论模型,除非你在处理某种物理问题或者某种你认为这实际上是世界如何运作的东西,否则没有……我不知道,我们是在真空中工作,有确切的重力等等。但是在现实世界中,事情是这样的——更好的方法是学习你的系数并计算它们。
Yannet:这个dual=True是什么[1:31:30]?我希望你会忽略,不会注意到,但你看到了。基本上,在这种情况下,我们的术语文档矩阵比高度更宽。逻辑回归有一个几乎在数学上等价的重新表述,当它比高度更宽时,速度会更快。简短的答案是,每当它比高度更宽时,加上dual=True,它会运行得更快。这只需要 2 秒。如果你不在这里加上它,那么需要几分钟。因此,在数学中,有一种问题的双重版本的概念,这些版本在某些情况下可能更适合。
这是二值化版本[1:32:20]。差不多一样。所以你可以看到我用术语文档矩阵的符号进行了拟合,并用val_term_doc.sign()进行了预测。
m = LogisticRegression(C=1e8, dual=True)
m.fit(trn_term_doc.sign(), y)
preds = m.predict(val_term_doc.sign())
(preds==val_y).mean()
'''
0.85487999999999997
'''
现在问题是,对于我们词汇表中大约有 75,000 个术语的每个术语都会有一个系数,考虑到我们只有 25,000 条评论,这似乎是很多系数[1:32:38]。所以也许我们应该尝试对此进行正则化。
所以我们可以使用内置在 sklearn 的 LogisticRegression 类中的正则化,它使用的参数是C。这有点奇怪,较小的参数表示更多的正则化。这就是为什么我使用1e8基本上关闭了正则化。

所以如果我打开正则化,将其设置为 0.1,那么现在是 88%:
m = LogisticRegression(C=0.1, dual=True)
m.fit(x, y)
preds = m.predict(val_term_doc)
(preds==val_y).mean()
'''
0.88275999999999999
'''
这是有道理的。你会认为对于 25,000 个文档的 75,000 个参数,很可能会过拟合。事实上,它确实过拟合了。因此,这是添加 L2 正则化以避免过拟合。
我之前提到过,除了 L2(查看权重的平方)之外,还有 L1(仅查看权重的绝对值)[1:33:37]。

我之前在措辞上有点粗心,我说 L2 试图将事物变为零。这在某种程度上是正确的,但如果你有两个高度相关的事物,那么 L2 正则化会将它们一起降低。它不会使其中一个变为零,另一个变为非零。因此,L1 正则化实际上具有这样的特性,它会尽可能使尽可能多的事物变为零,而 L2 正则化具有这样的特性,它倾向于使一切变得更小。实际上,在任何现代机器学习中,我们并不关心这种差异,因为我们很少直接尝试解释系数。我们尝试通过我们学到的技术来审查我们的模型。我们关心 L1 与 L2 的原因仅仅是哪一个在验证集上的错误更小。你可以尝试两种方法。使用 sklearn 的 LogisticRegression,L2 实际上会更快,因为你不能使用dual=True,除非你使用 L2,而 L2 是默认的。所以我并没有太担心这种差异。
所以你可以看到,如果我们使用正则化和二值化,我们实际上做得相当不错:
m = LogisticRegression(C=0.1, dual=True)
m.fit(trn_term_doc.sign(), y)
preds = m.predict(val_term_doc.sign())
(preds==val_y).mean()
'''
0.88404000000000005
'''
问题:在我们学习关于类似于组合 L1 和 L2 的 Elastic-net 之前。我们可以这样做吗?是的,你可以这样做,但需要更深层次的模型。我从来没有见过有人发现这有用。
最后我要提到的是,当你做 CountVectorizer 时,你也可以要求 n-gram。默认情况下,我们得到的是单字,也就是单个单词。但是如果我们说ngram_range=(1,3),那也会给我们二元组和三元组。
veczr = CountVectorizer(
ngram_range=(1,3),
tokenizer=tokenize,
max_features=800000
)
trn_term_doc = veczr.fit_transform(trn)
val_term_doc = veczr.transform(val)
trn_term_doc.shape
'''
(25000, 800000)
'''
vocab = veczr.get_feature_names()
vocab[200000:200005]
'''
['by vast', 'by vengeance', 'by vengeance .', 'by vera', 'by vera miles']
'''
也就是说,如果我现在说好的,让我们继续使用 CountVectorizer,并获取特征名称,现在我的词汇表包括二元组:'by vast','by vengeance'和三元组:'by vengeance .','by vera miles'。所以现在做的事情与之前相同,但在分词之后,它不仅仅是抓取每个单词并说这是你的词汇表的一部分,而是抓取相邻的每两个单词和每三个单词。这实际上对利用词袋方法非常有帮助,因为我们现在可以看到not good与not bad与not terrible之间的区别。甚至像"good"这样的词可能是讽刺的。因此,实际上使用三元组特征将使朴素贝叶斯和逻辑回归变得更好。这确实让我们走得更远,使它们变得更有用。
问题:我有一个关于分词器的问题。你说max_features,那么这些二元组和三元组是如何选择的?由于我使用的是线性模型,我不想创建太多特征。即使没有max_features,它实际上也可以正常工作。我想我有大约 7000 万个系数。它仍然有效。但没有必要有 7000 万个系数。所以如果你说max_features=800,000,CountVectorizer 将按照所有内容出现的频率对词汇表进行排序,无论是单字、二元组还是三元组,然后在前 800,000 个最常见的 n 元组之后截断。N-gram 只是单字、二元组和三元组的通用词。

所以这就是为什么train_term_doc.shape现在是 25,000 乘以 800,000。如果你不确定最大值应该是多少,我只是选择了一个非常大的数字,不太担心,似乎也没问题。这并不是非常敏感的。
好了,我们时间到了,明天我们将看到什么…顺便说一句,我们可以用我们的 PyTorch 版本替换这个 LogisticRegression:

明天,我们实际上会在 Fast AI 库中看到一个可以做到这一点的东西,但明天我们还将看到如何将逻辑回归和朴素贝叶斯结合在一起,以获得比任何一个都更好的结果。然后我们将学习如何从那里开始创建一个更深层的神经网络,以获得几乎是结构化学习的最新结果。好的,到时候见。


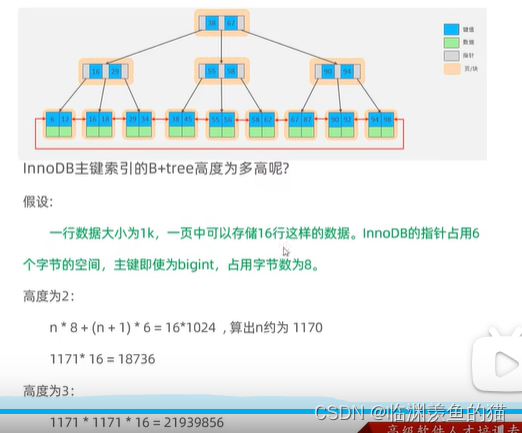

![[韩顺平]python笔记](https://img-blog.csdnimg.cn/direct/3f38a8bb9fa9437fbe4b3b7b6b4056ea.png)

