🎇个人主页:Ice_Sugar_7
🎇所属专栏:Java数据结构
🎇欢迎点赞收藏加关注哦!
实现BST
- 🍉二叉搜索树的性质
- 🍉实现二叉搜索树
- 🍌插入
- 🍌查找
- 🍌删除
- 🍉性能分析
🍉二叉搜索树的性质
二叉搜索树又称二叉排序树,它可以是一棵空树,也可以是有以下性质的二叉树
- 若左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
因为左节点 < 根节点 < 右节点,所以二叉搜索树中序遍历结果是升序序列
🍉实现二叉搜索树
🍌插入
插入成功返回true,插入失败返回false
(注意:如果树中已经有关键字key,那我们就不能再插入了)
//插入一个关键字key
public boolean insert(int key) {
TreeNode node = new TreeNode(key);
if(root == null) {
root = node;
return true;
}
TreeNode cur = root;
TreeNode parent = null; //保存cur的双亲节点
while(cur != null) { //cur若为空,说明找到插入位置了
if(cur.key < key) {
parent = cur;
cur = cur.right;
} else if(cur.key > key) {
parent = cur;
cur = cur.left;
} else { //树中已经有key,不能插入
return false;
}
}
//比较key和双亲节点的key,确定key要插在parent的左边还是右边
if(key > parent.key)
parent.right = node;
if(key < parent.key)
parent.left = node;
return true;
}
🍌查找
根据二叉搜索树的特点,key比当前节点的值小,就往左子树找;反之则往右子树找
//查找key是否存在
public TreeNode search(int key) {
if(root == null)
return null;
TreeNode cur = root;
while(cur != null) {
if(cur.key < key) {
cur = cur.right;
} else if(cur.key > key) {
cur = cur.left;
} else {
return cur;
}
}
return null; //到这里说明找不到,返回null
}
🍌删除
这个操作比较麻烦,因为它需要处理多种情况。大方向上分为三种情况讨论:
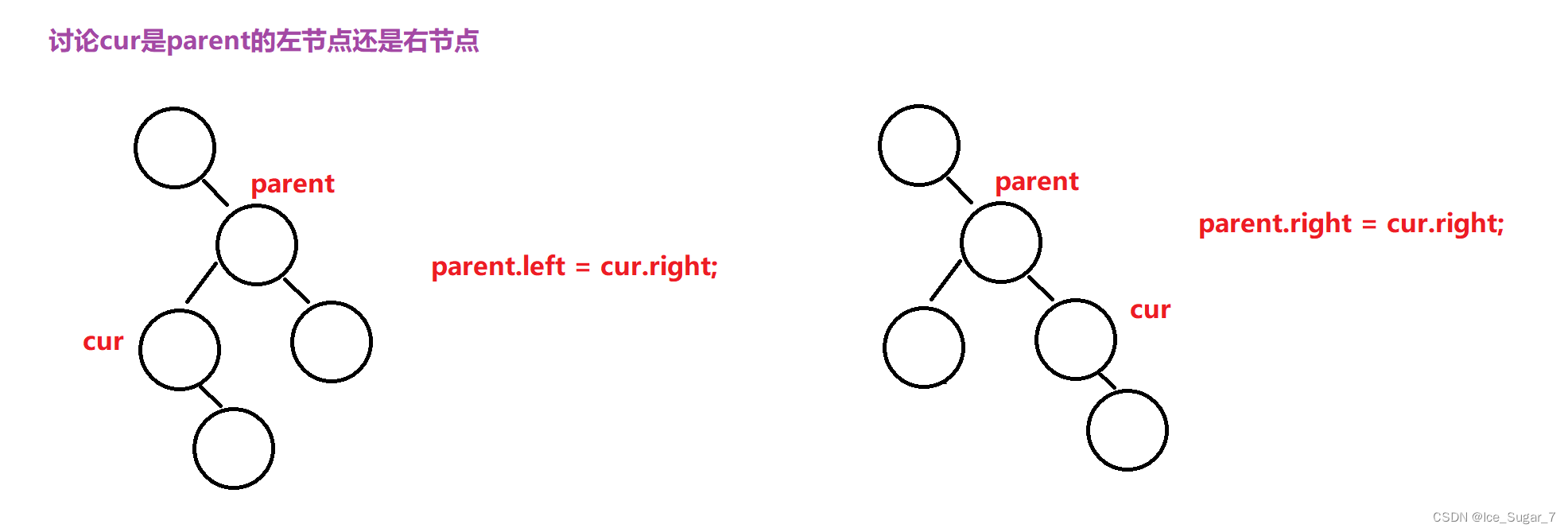
假设根节点为root,待删除节点是cur,它的双亲节点为parent
-
cur的左节点为空
①cur就是根节点(此时parent不存在),只需让root = root.right
②cur不是根节点,是parent的左节点
③cur不是根节点,是parent的右节点
②和③的分析如下图:
-
cur的右节点为空
这个和1的分析思路是一样的,就不多赘述了 -
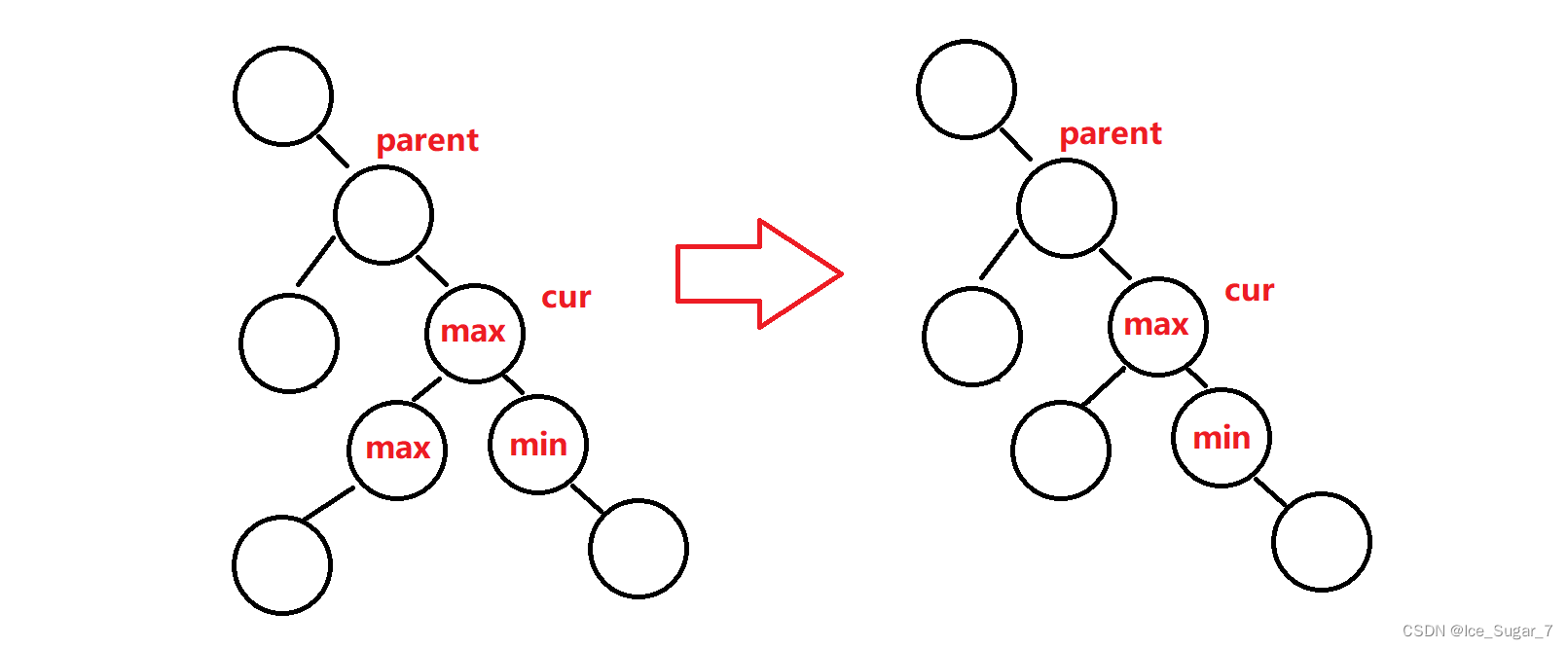
cur的左右节点都不为空
使用替换法进行删除:
就是从cur的左子树中找到最右侧的节点(这个节点是左子树中关键字最大的)max,或者从右子树中找到最左侧节点(关键字最小)min,用它的值替换掉cur的值,然后再把max或min删掉
其实就是转化为1和2的问题,因为max和min的左节点和右节点肯定有一个为空
来看下代码实现:
//删除key的值
public boolean remove(int key) {
if(root == null)
return false;
TreeNode cur = root;
TreeNode parent = null;
while(cur != null) {
if(cur.key < key) {
parent = cur;
cur = cur.right;
} else if(cur.key > key) {
parent = cur;
cur = cur.left;
} else { //找到cur了,准备把它删了
if(cur.left == null) {
if(cur == root) {
root = root.right;
return true;
} else {
if(cur == parent.left)
parent.left = cur.right;
if(cur == parent.right)
parent.right = cur.right;
}
} else if(cur.right == null) {
if(cur == root) {
root = root.left;
return true;
} else {
if(cur == parent.left)
parent.left = cur.left;
if(cur == parent.right)
parent.right = cur.left;
}
} else { //左右都不为空
TreeNode target = cur.right; //让target去右子树找到最左边的节点
TreeNode targetParent = cur;
while(target.left != null) {
targetParent = target;
target = target.left;
}
//将tmp的关键字赋给cur
cur.key = target.key;
//删除tmp节点
if(targetParent.left == target) {
targetParent.left = cur.right;
} else {
targetParent.right = cur.right;
}
}
return true;
}
}
return false;
}
🍉性能分析
插入和删除等操作都必须先查找,所以查找的效率代表二叉搜索树中各个操作的性能
每次查找都要比较key和当前节点的值。
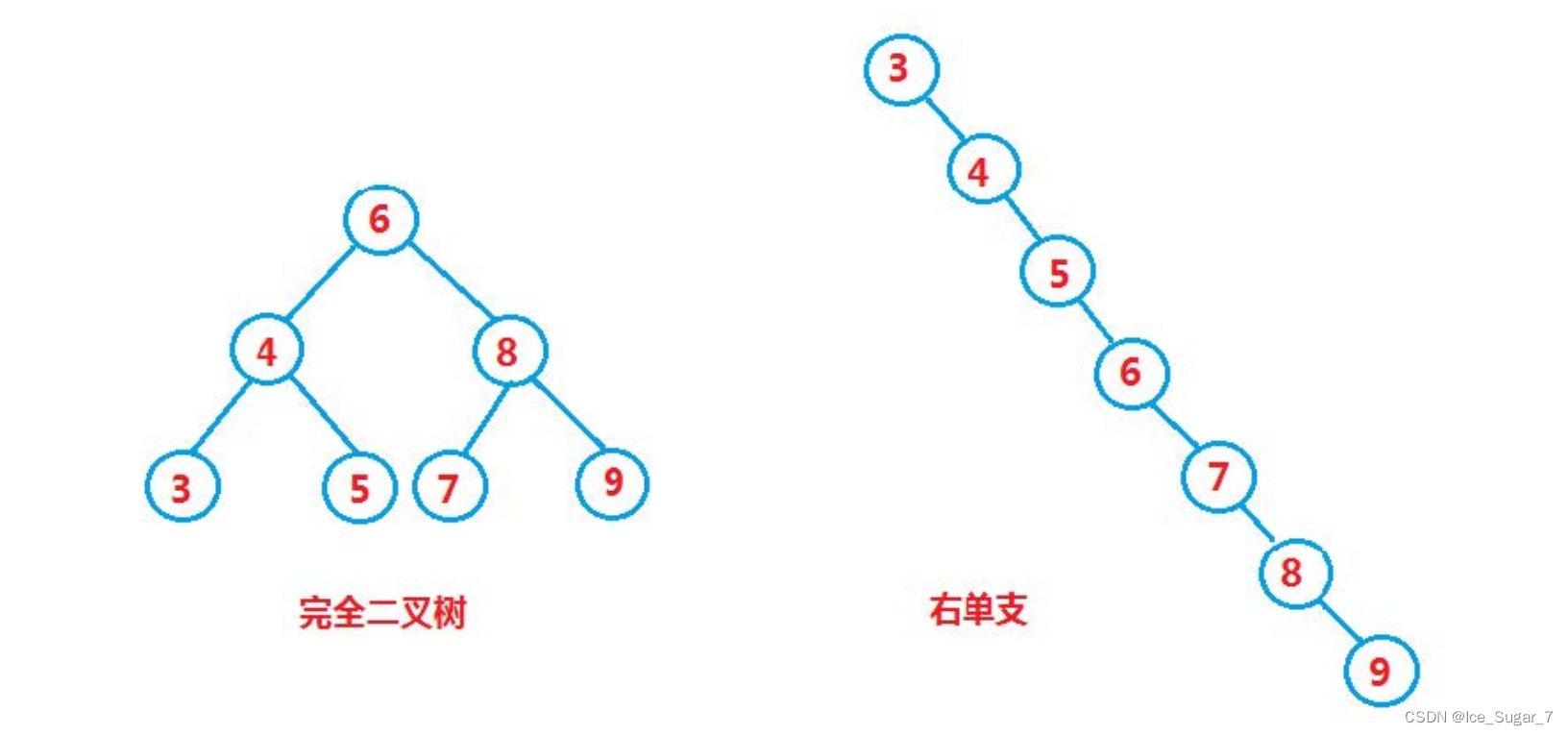
那么在最好的情况下,二叉搜索树是完全二叉树,平均比较次数是logN
而在最坏的情况下,此时二叉搜索树退化为单支树,平均比较次数就是N / 2


![[韩顺平]python笔记](https://img-blog.csdnimg.cn/direct/3f38a8bb9fa9437fbe4b3b7b6b4056ea.png)



![[经验] 喉咙沙哑的原因及应对方法是什么 #学习方法#其他#媒体](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=https%3A%2F%2Fwww.hao123rr.com%2Fzb_users%2Fupload%2F2023%2F05%2F20230523114808168481368889679.jpg&pos_id=Hpc4kCSl)